Difference between revisions of "1985 AIME Problems/Problem 15"
Mathgeek2006 (talk | contribs) m (→Solution) |
m (→Solution) |
||
| Line 5: | Line 5: | ||
== Solution == | == Solution == | ||
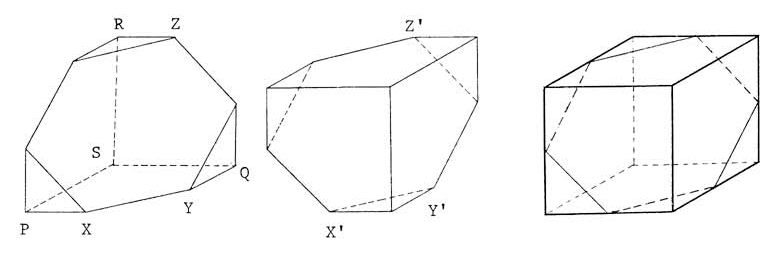
| − | Note that gluing two of the given polyhedra together along a hexagonal face (rotated <math>60^\circ</math> from each other) yields a [[cube (geometry) | cube]], so the volume is <math>\frac12 \cdot 12^3 = 864</math>. | + | Note that gluing two of the given polyhedra together along a hexagonal face (rotated <math>60^\circ</math> from each other) yields a [[cube (geometry) | cube]], so the volume is <math>\frac12 \cdot 12^3 = 864</math>, so our answer is <math>\boxed{864}</math>. |
Image: [[Image:AoPS_AIME_1985.png]] | Image: [[Image:AoPS_AIME_1985.png]] | ||
Revision as of 12:34, 29 December 2019
Problem
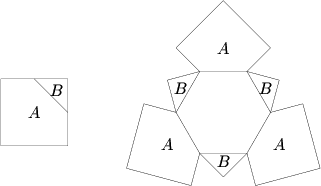
Three 12 cm 
12 cm squares are each cut into two pieces 
and 
, as shown in the first figure below, by joining the midpoints of two adjacent sides. These six pieces are then attached to a regular hexagon, as shown in the second figure, so as to fold into a polyhedron. What is the volume (in 
) of this polyhedron?
Solution
Note that gluing two of the given polyhedra together along a hexagonal face (rotated 
from each other) yields a cube, so the volume is 
, so our answer is 
.
Image: 
See also
| 1985 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 14 |
Followed by Last Question | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
