Difference between revisions of "1987 AIME Problems/Problem 9"

Revision as of 16:27, 18 January 2020

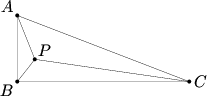
Problem

Triangle $ABC$ has right angle at $B$ , and contains a point $P$ for which $PA = 10$ , $PB = 6$ , and $\angle APB = \angle BPC = \angle CPA$ . Find $PC$ .

Solution

Let $PC = x$ . Since $\angle APB = \angle BPC = \angle CPA$ , each of them is equal to $120^\circ$ . By the Law of Cosines applied to triangles $\triangle APB$ , $\triangle BPC$ and $\triangle CPA$ at their respective angles $P$ , remembering that $\cos 120^\circ = -\frac12$ , we have

$AB^2 = 36 + 100 + 60 = 196, BC^2 = 36 + x^2 + 6x, CA^2 = 100 + x^2 + 10x$

Then by the Pythagorean Theorem, $AB^2 + BC^2 = CA^2$ , so

$x^2 + 10x + 100 = x^2 + 6x + 36 + 196$

and

$4x = 132 \Longrightarrow x = \boxed{033}.$

Note

This is the Fermat point of the triangle

@@ Line 15: / Line 15: @@
 <cmath>4x = 132 \Longrightarrow x = \boxed{033}.</cmath>
+== Note ==
+This is the Fermat point of the triangle
 == See also ==

1987 AIME (Problems • Answer Key • Resources)
Preceded by Problem 8	Followed by Problem 10
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

Page

Toolbox

Search

Difference between revisions of "1987 AIME Problems/Problem 9"

Revision as of 16:27, 18 January 2020

Contents

Problem

Solution

Note

See also