Difference between revisions of "2010 AMC 12A Problems/Problem 8"
(Tag: Undo) |
|||
| Line 18: | Line 18: | ||
Since <math>\frac{AC}{AB} = \frac{1}{2}</math>, triangle <math>ABC</math> is a <math>30-60-90</math> triangle, so <math>\angle BCA = \boxed{90^\circ\,\textbf{(C)}}</math>. | Since <math>\frac{AC}{AB} = \frac{1}{2}</math>, triangle <math>ABC</math> is a <math>30-60-90</math> triangle, so <math>\angle BCA = \boxed{90^\circ\,\textbf{(C)}}</math>. | ||
| + | == Solution 2(Trig and Angle Chasing) == | ||
| + | Let <math>AB=2a, AC=a</math>. Let <math>\angle BAE=\angle ACD=x</math>. Because <math>\triangle CFE</math> is equilateral, we get <math>\angle FCE=60</math>, so <math>\angle ACB=60+x</math>. Because <math>\triangle CFE</math> is equilateral, we get <math>\angle CFE=60</math>. Angles <math>AFD</math> and <math>CFE</math> are vertical, so <math>\angle AFD=60</math>. By triangle <math>ADF</math>, we have <math>\angle ADF=120-x</math>, and because of line <math>AB</math>, we have <math>\angle BDC=60+x</math>. Because Of line <math>BC</math>, we have <math>\angle AEB=120</math>, and by line <math>CD</math>, we have <math>\angle DFE=120</math>. By quadrilateral <math>BDFE</math>, we have <math>\angle ABC=60-x</math>. | ||
| + | By the Law of Sines, we have <math>\frac{\sin(60-x)}{a}=\frac{\sin(60+x)}{2a}\implies </math>\sin(60-x)=\frac{\sin(60+x)}{2}\implies 2\sin(60-x)=\sin(60+x)<math>. By the sine addition formula(which states </math>\sin(a+b)=\sin(a)\cos(b)+\cos(a)\sin(b)<math> by the way), we have </math>2(\sin(60)\cos(-x)+\cos(60)\sin(-x))=\sin(60)\cos(x)+\cos(60)\sin(x)<math>. Because cosine is an even function, and sine is an odd function, we have </math>2\sin(60)\cos(x)-2\cos(60)\sin(x)=\sin(60)\cos(x)+\cos(60)\sin(x) \implies \sin(60)\cos(x)=3\cos(60)\sin(x)<math>. We know that </math>\sin(60)=\frac{\sqrt{3}}{2}<math>, and </math>\cos(60)=\frac{1}{2}<math>, hence </math>\frac{\sqrt{3}}{2}\cos(x)=\frac{3}{2}\sin(x)\implies <math>\tan(x)=\frac{\sqrt(3)}{3}</math>. The only value of <math>x</math> that satisfies <math>60+x<180</math>(because <math>60+x</math> is an angle of the triangle)<math> is </math>x=30^{\circ}<math>. We seek to find </math>\angle ACB<math>, which as we found before is </math>60+x<math>, which is </math>90$. The answer is (C) | ||
| + | |||
| + | -vsamc | ||
== See also == | == See also == | ||
{{AMC12 box|year=2010|num-b=7|num-a=9|ab=A}} | {{AMC12 box|year=2010|num-b=7|num-a=9|ab=A}} | ||
Revision as of 16:39, 10 March 2020
Problem
Triangle ![]() has
has ![]() . Let
. Let ![]() and
and ![]() be on
be on ![]() and
and ![]() , respectively, such that
, respectively, such that ![]() . Let
. Let ![]() be the intersection of segments
be the intersection of segments ![]() and
and ![]() , and suppose that
, and suppose that ![]() is equilateral. What is
is equilateral. What is ![]() ?
?
![]()
Solution
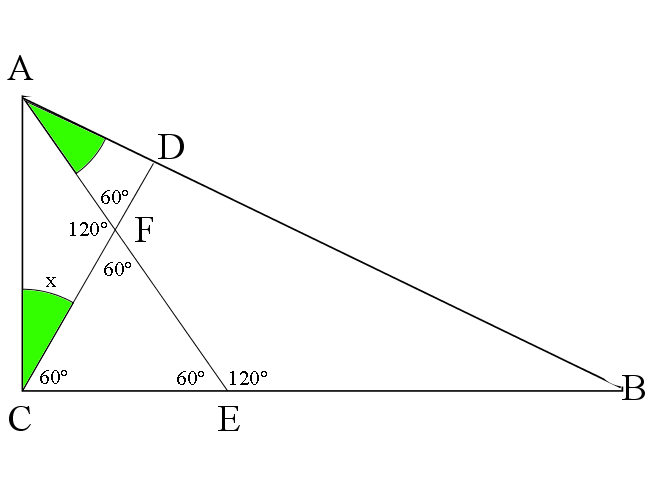
Let ![]() .
.

Since ![]() , triangle
, triangle ![]() is a
is a ![]() triangle, so
triangle, so ![]() .
.
Solution 2(Trig and Angle Chasing)
Let ![]() . Let
. Let ![]() . Because
. Because ![]() is equilateral, we get
is equilateral, we get ![]() , so
, so ![]() . Because
. Because ![]() is equilateral, we get
is equilateral, we get ![]() . Angles
. Angles ![]() and
and ![]() are vertical, so
are vertical, so ![]() . By triangle
. By triangle ![]() , we have
, we have ![]() , and because of line
, and because of line ![]() , we have
, we have ![]() . Because Of line
. Because Of line ![]() , we have
, we have ![]() , and by line
, and by line ![]() , we have
, we have ![]() . By quadrilateral
. By quadrilateral ![]() , we have
, we have ![]() .
.
By the Law of Sines, we have ![]() \sin(60-x)=\frac{\sin(60+x)}{2}\implies 2\sin(60-x)=\sin(60+x)
\sin(60-x)=\frac{\sin(60+x)}{2}\implies 2\sin(60-x)=\sin(60+x)![]() \sin(a+b)=\sin(a)\cos(b)+\cos(a)\sin(b)
\sin(a+b)=\sin(a)\cos(b)+\cos(a)\sin(b)![]() 2(\sin(60)\cos(-x)+\cos(60)\sin(-x))=\sin(60)\cos(x)+\cos(60)\sin(x)
2(\sin(60)\cos(-x)+\cos(60)\sin(-x))=\sin(60)\cos(x)+\cos(60)\sin(x)![]() 2\sin(60)\cos(x)-2\cos(60)\sin(x)=\sin(60)\cos(x)+\cos(60)\sin(x) \implies \sin(60)\cos(x)=3\cos(60)\sin(x)
2\sin(60)\cos(x)-2\cos(60)\sin(x)=\sin(60)\cos(x)+\cos(60)\sin(x) \implies \sin(60)\cos(x)=3\cos(60)\sin(x)![]() \sin(60)=\frac{\sqrt{3}}{2}
\sin(60)=\frac{\sqrt{3}}{2}![]() \cos(60)=\frac{1}{2}
\cos(60)=\frac{1}{2}![]() \frac{\sqrt{3}}{2}\cos(x)=\frac{3}{2}\sin(x)\implies
\frac{\sqrt{3}}{2}\cos(x)=\frac{3}{2}\sin(x)\implies ![]() . The only value of
. The only value of ![]() that satisfies
that satisfies ![]() (because
(because ![]() is an angle of the triangle)
is an angle of the triangle)![]() x=30^{\circ}
x=30^{\circ}![]() \angle ACB
\angle ACB![]() 60+x
60+x![]() 90$. The answer is (C)
90$. The answer is (C)
-vsamc
See also
| 2010 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 7 |
Followed by Problem 9 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. ![]()









