Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus
During AMC testing, the AoPS Wiki is in read-only mode and no edits can be made.

Difference between revisions of "2018 IMO Problems/Problem 6"

(→‎Solution)
(→‎Solution)
Line 6: Line 6:
 
==Solution==
 
==Solution==
 
[[File:2018 IMO 6.png|490px|right]]
 
[[File:2018 IMO 6.png|490px|right]]
 +
[[File:2018 IMO 6 Claim 3.png|370px|right]]
 
<i><b>Special case</b></i>
 
<i><b>Special case</b></i>
  
Line 20: Line 21:
 
<math>\angle FCX =  \angle BCX</math> subtend the arc <math>\overset{\Large\frown} {XF}</math> of <math>\omega, \angle CBX = \angle XDA</math> subtend the arc <math>\overset{\Large\frown} {XF}</math> of <math>\Omega.</math> The sum of these arcs is <math>180^\circ</math>  <i><b>(Claim 3).</b></i>.  
 
<math>\angle FCX =  \angle BCX</math> subtend the arc <math>\overset{\Large\frown} {XF}</math> of <math>\omega, \angle CBX = \angle XDA</math> subtend the arc <math>\overset{\Large\frown} {XF}</math> of <math>\Omega.</math> The sum of these arcs is <math>180^\circ</math>  <i><b>(Claim 3).</b></i>.  
  
−
Hence, the sum of the arcs XF is 180°, the sum of the angles ∠XСВ + ∠XВС = 90°, ∠СХВ = 90°. Similarly, ∠AXD = 90°, that is, ∠BXA + ∠DXC = 180°.
+
Hence, the sum of the arcs <math>\overset{\Large\frown} {XF}</math>  is <math>180^\circ \implies</math>
  
−
<i><b>Claim 1</b></i>
+
the sum <math>\angle XCB + \angle XBC = 90^\circ \implies \angle CXB = 90^\circ.</math>
  
−
Let A, C, and E be arbitrary points on a circle ω, l be the middle perpendicular to the segment AC. Then the straight lines AE and CE intersect l at the points B and D, symmetric with respect to ω.
+
Similarly, <math>\angle AXD =  90^\circ \implies \angle BXA + \angle DXC = 180^\circ.</math>
 +
 
 +
<i><b>Claim 1</b></i> Let A, C, and E be arbitrary points on a circle ω, l be the middle perpendicular to the segment AC. Then the straight lines AE and CE intersect l at the points B and D, symmetric with respect to ω.
 +
 
 +
<i><b>Claim 2</b></i> Let points B and D be symmetric with respect to the circle ω. Then any circle Ω passing through these points is orthogonal to ω.
 +
 
 +
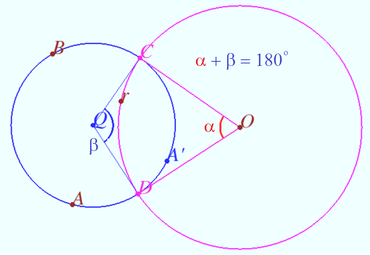
<i><b>Claim 3</b></i> The sum of the arcs between the points of intersection of two perpendicular circles is <math>180^\circ.</math>
 +
In the figure they are a blue and red arcs CD, α + β = 180°.

Revision as of 13:20, 17 August 2022

A convex quadrilateral $ABCD$ satisfies $AB\cdot CD=BC \cdot DA.$ Point $X$ lies inside $ABCD$ so that $\angle XAB = \angle XCD$ and $\angle XBC = \angle XDA.$ Prove that $\angle BXA + \angle DXC = 180^{\circ}$

Solution

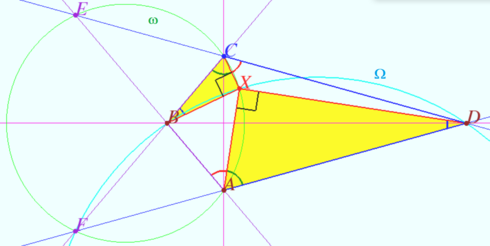
2018 IMO 6.png
2018 IMO 6 Claim 3.png

Special case

We construct point $X_0$ and prove that $X_0$ coincides with the point $X.$

Let $AD = CD$ and $AB = BC \implies AB \cdot CD = BC \cdot DA.$

Let $E$ and $F$ be the intersection points of $AB$ and $CD,$ and $BC$ and $DA,$ respectively.

The points $B$ and $D$ are symmetric with respect to the circle $\omega = EACF$ (Claim 1). The circle $\Omega = FBD$ is orthogonal to the circle $\omega$ (Claim 2). Let $X_0$ be the point of intersection of the circles $\omega$ and $\Omega.$ $\angle X_0AB = \angle X_0CD$ (quadrilateral $AX_0CF$ is cyclic) and $\angle X_0BC = \angle X_0DA$ (quadrangle $DX_0BF$ is cyclic). This means that $X_0$ coincides with the point $X$ indicated in the condition.

$\angle FCX = \angle BCX$ subtend the arc $\overset{\Large\frown} {XF}$ of $\omega, \angle CBX = \angle XDA$ subtend the arc $\overset{\Large\frown} {XF}$ of $\Omega.$ The sum of these arcs is $180^\circ$ (Claim 3)..

Hence, the sum of the arcs $\overset{\Large\frown} {XF}$ is $180^\circ \implies$

the sum $\angle XCB + \angle XBC = 90^\circ \implies \angle CXB = 90^\circ.$

Similarly, $\angle AXD = 90^\circ \implies \angle BXA + \angle DXC = 180^\circ.$

Claim 1 Let A, C, and E be arbitrary points on a circle ω, l be the middle perpendicular to the segment AC. Then the straight lines AE and CE intersect l at the points B and D, symmetric with respect to ω.

Claim 2 Let points B and D be symmetric with respect to the circle ω. Then any circle Ω passing through these points is orthogonal to ω.

Claim 3 The sum of the arcs between the points of intersection of two perpendicular circles is $180^\circ.$ In the figure they are a blue and red arcs CD, α + β = 180°.

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2018_IMO_Problems/Problem_6&oldid=177102"