Difference between revisions of "2018 IMO Problems/Problem 6"
(→Solution) |
(→Solution) |
||
| Line 84: | Line 84: | ||
Denote <math>\angle XAB = \angle XCD = \alpha, \angle BXA = \varphi, \angle DXC = \psi.</math> | Denote <math>\angle XAB = \angle XCD = \alpha, \angle BXA = \varphi, \angle DXC = \psi.</math> | ||
| − | By the law of sines for | + | By the law of sines for <math>\triangle ABX,</math> we obtain <math>\frac {AB}{\sin \varphi} = \frac{BX}{\sin \alpha}.</math> |
| + | |||
| + | By the law of sines for <math>\triangle CDX,</math> we obtain <math>\frac {CD}{\sin \psi} = \frac {DX}{\sin \alpha}.</math> | ||
| + | |||
| + | We make transformation and get <cmath>{\sin \psi} = \frac {CD}{DX} {\sin \alpha} = \frac{CD}{DX} \cdot {\frac{DX \cdot AB}{BX \cdot CD}} {\sin \alpha} = \frac {AB}{BX}\sin \alpha = \sin \psi.</cmath> | ||
Revision as of 08:08, 19 August 2022
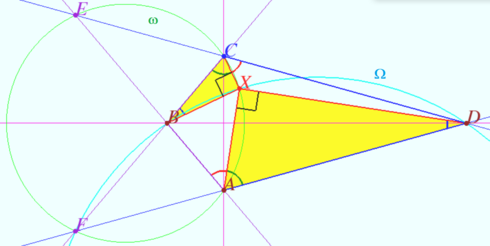
A convex quadrilateral ![]() satisfies
satisfies ![]() Point
Point ![]() lies inside
lies inside
![]() so that
so that
![]() and
and ![]() Prove that
Prove that ![]()
Solution
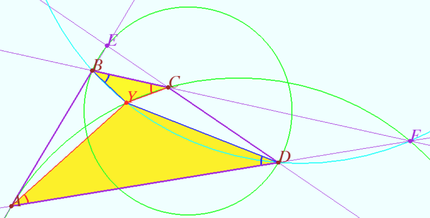
Special case
We construct point ![]() and prove that
and prove that ![]() coincides with the point
coincides with the point ![]()
Let ![]() and
and ![]()
Let ![]() and
and ![]() be the intersection points of
be the intersection points of ![]() and
and ![]() and
and ![]() and
and ![]() respectively.
respectively.
The points ![]() and
and ![]() are symmetric with respect to the circle
are symmetric with respect to the circle ![]() (Claim 1).
(Claim 1).
The circle ![]() is orthogonal to the circle
is orthogonal to the circle ![]() (Claim 2).
(Claim 2).
Let ![]() be the point of intersection of the circles
be the point of intersection of the circles ![]() and
and ![]() Quadrilateral
Quadrilateral ![]() is cyclic
is cyclic ![]()
![]()
Similarly, quadrangle ![]() is cyclic
is cyclic ![]() .
.
This means that point ![]() coincides with the point
coincides with the point ![]() .
.
![]() of
of ![]()
![]() of
of ![]()
The sum ![]() (Claim 3)
(Claim 3) ![]()
![]()
Similarly, ![]()
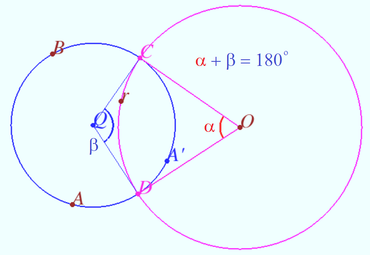
Claim 1 Let ![]() and
and ![]() be arbitrary points on a circle
be arbitrary points on a circle ![]() be the middle perpendicular to the segment
be the middle perpendicular to the segment ![]() Then the straight lines
Then the straight lines ![]() and
and ![]() intersect
intersect ![]() at the points
at the points ![]() and
and ![]() symmetric with respect to
symmetric with respect to ![]()
Claim 2 Let points ![]() and
and ![]() be symmetric with respect to the circle
be symmetric with respect to the circle ![]() Then any circle
Then any circle ![]() passing through these points is orthogonal to
passing through these points is orthogonal to ![]()
Claim 3 The sum of the arcs between the points of intersection of two perpendicular circles is ![]() In the figure they are a blue and red arcs
In the figure they are a blue and red arcs ![]()
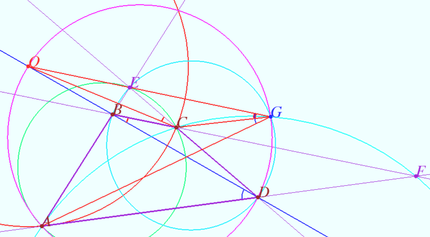
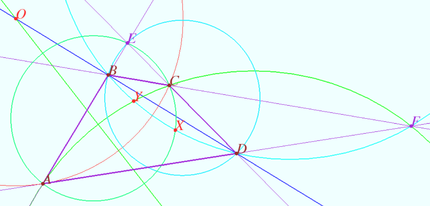
Common case
Denote by ![]() the intersection point of the perpendicular bisector of
the intersection point of the perpendicular bisector of ![]() and
and ![]() Let
Let ![]() be a circle (red) with center
be a circle (red) with center ![]() and radius
and radius ![]()
The points ![]() and
and ![]() are symmetric with respect to the circle
are symmetric with respect to the circle ![]() (Claim 1).
(Claim 1).
The circles ![]() and
and ![]() are orthogonal to the circle
are orthogonal to the circle ![]() (Claim 2).
(Claim 2).
Circles ![]() and
and ![]() are symmetric with respect to the circle
are symmetric with respect to the circle ![]() (Lemma).
(Lemma).
Denote by ![]() the point of intersection of the circles
the point of intersection of the circles ![]() and
and ![]() Quadrangle
Quadrangle ![]() is cyclic
is cyclic ![]() (see Special case).
Similarly, quadrangle
(see Special case).
Similarly, quadrangle ![]() is cyclic
is cyclic ![]()
The required point ![]() is constructed.
is constructed.
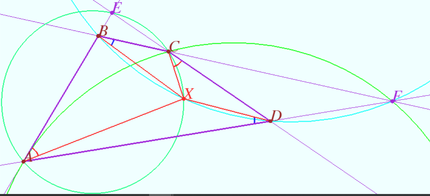
Denote by ![]() the point of intersection of circles
the point of intersection of circles ![]() and
and ![]()
Quadrangle ![]() is cyclic
is cyclic ![]()
Quadrangle ![]() is cyclic
is cyclic ![]()
The triangles ![]() by two angles, so
by two angles, so ![]()
The points ![]() and
and ![]() are symmetric with respect to the circle
are symmetric with respect to the circle ![]() , since they lie on the intersection of the circles
, since they lie on the intersection of the circles ![]() and
and ![]() symmetric with respect to
symmetric with respect to ![]() and the orthogonal
and the orthogonal ![]() circle
circle ![]()
The point ![]() is symmetric to itself, the point
is symmetric to itself, the point ![]() is symmetric to
is symmetric to ![]() with respect to
with respect to ![]() Usung
Usung ![]() and the equality
and the equality ![]() we get
we get ![]() The point
The point ![]() is symmetric to itself, the point
is symmetric to itself, the point ![]() is symmetric to
is symmetric to ![]() with respect to
with respect to ![]()
![]()
![]() The point
The point ![]() is symmetric to
is symmetric to ![]() and the point
and the point ![]() is symmetric to
is symmetric to ![]() with respect to
with respect to ![]() hence
hence
![]()
![]() Denote
Denote ![]()
By the law of sines for ![]() we obtain
we obtain ![]()
By the law of sines for ![]() we obtain
we obtain ![]()
We make transformation and get ![]()