Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus
During AMC testing, the AoPS Wiki is in read-only mode and no edits can be made.

Difference between revisions of "2018 IMO Problems/Problem 6"

(→‎Solution)
(→‎Solution)
Line 40: Line 40:
 
[[File:2018 IMO 6c.png|430px|right]]
 
[[File:2018 IMO 6c.png|430px|right]]
 
[[File:2018 IMO 6d.png|430px|right]]
 
[[File:2018 IMO 6d.png|430px|right]]
−
[[File:2018 IMO 6 Claim 3.png|370px|right]]
+
 
 
<i><b>Common case </b></i>
 
<i><b>Common case </b></i>
  
Line 87: Line 87:
 
In all other cases, the equality of the sines follows <math>\psi = 180° – \varphi \implies \varphi + \psi = 180°.</math>
 
In all other cases, the equality of the sines follows <math>\psi = 180° – \varphi \implies \varphi + \psi = 180°.</math>
  
 +
[[File:2018 IMO 6 Claim 3.png|370px|right]]
 +
[[File:2018 IMO 6a.png|430px|right]]
 
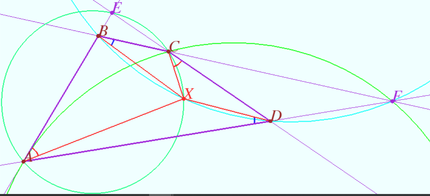
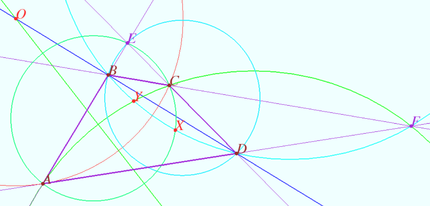
<i><b>Claim 1</b></i> Let <math>A, C,</math> and <math>E</math> be arbitrary points on a circle <math>\omega, l</math> be the perpendicular bisector to the segment <math>AC.</math> Then the straight lines <math>AE</math> and <math>CE</math> intersect <math>l</math> at the points <math>B</math> and <math>D,</math> symmetric with respect to <math>\omega.</math>
 
<i><b>Claim 1</b></i> Let <math>A, C,</math> and <math>E</math> be arbitrary points on a circle <math>\omega, l</math> be the perpendicular bisector to the segment <math>AC.</math> Then the straight lines <math>AE</math> and <math>CE</math> intersect <math>l</math> at the points <math>B</math> and <math>D,</math> symmetric with respect to <math>\omega.</math>
  
Line 93: Line 95:
 
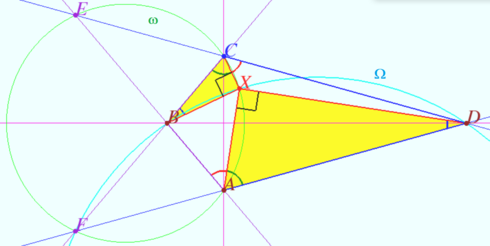
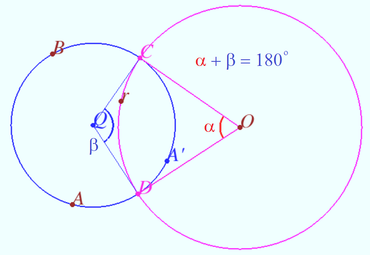
<i><b>Claim 3</b></i> The sum of the arcs between the points of intersection of two perpendicular circles is <math>180^\circ.</math>
 
<i><b>Claim 3</b></i> The sum of the arcs between the points of intersection of two perpendicular circles is <math>180^\circ.</math>
 
In the figure they are a blue and red arcs <math>\overset{\Large\frown} {CD}, \alpha + \beta = 180^\circ.</math>
 
In the figure they are a blue and red arcs <math>\overset{\Large\frown} {CD}, \alpha + \beta = 180^\circ.</math>
 +
 +
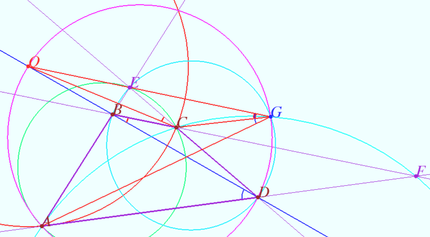
<i><b>Lemma</b></i> The opposite sides of the quadrilateral <math>ABCD</math> intersect at points <math>E</math> and <math>F</math> (<math>E</math> lies on <math>AB</math>). The circle  <math>\omega</math> centered at the point <math>O</math> contains the ends of the diagonal <math>AC.</math> The points <math>B</math> and <math>D</math> are symmetric with respect to the circle <math>\omega</math> (in other words, the inversion with respect to <math>\omega</math> maps <math>B</math> into <math>D).</math> Then the circles <math>ACE</math> and <math>ACF</math> are symmetric with respect to <math>\omega.</math>
 +
<i><b>Proof</b></i>
 +
We will prove that the point <math>G,</math> symmetric to the point <math>E</math> with respect to <math>\omega,</math> belongs to the circle <math>ACF.</math> For this, we will prove the equality <math>\angle AGC = \angle AFC.</math>
 +
 +
A circle <math>BDE</math> containing points <math>B</math> and <math>D</math> symmetric with respect to <math>\omega,</math> is orthogonal to <math>\omega</math> (Claim  2) and maps into itself under inversion with respect to the circle <math>\omega.</math> Hence, the point <math>E</math> under this inversion passes to some point <math>G,</math> of the same circle <math>BDE.</math>
 +
 +
A straight line <math>ABE</math> containing the point <math>A</math> of the circle <math>\omega,</math> under inversion with respect to <math>\omega,</math> maps into the circle <math>OADG.</math> Hence, the inscribed angles of this circle are equal  <math>\angle ADB =  \angle AGE.</math>
 +
<math>\angle OCE =  \angle CGE (CE</math> maps into <math>CG)</math> and  <math>\angle OCE =  \angle BCD (BC</math> maps into <math>DC).</math>
 +
Consequently, the angles  <math>\angle AFC =  \angle ADB –  \angle FBD =  \angle AGE -  </math>\angle CGE =  <math>\angle AGC.</math>
 +
These angles subtend the <math>\overset{\Large\frown} {AC}</math> of the <math>ACF</math> circle, that is, the point <math>G,</math> symmetric to the point <math>E</math> with respect to <math>\omega,</math> belongs to the circle <math>ACF.</math>

Revision as of 12:01, 19 August 2022

A convex quadrilateral $ABCD$ satisfies $AB\cdot CD=BC \cdot DA.$ Point $X$ lies inside $ABCD$ so that $\angle XAB = \angle XCD$ and $\angle XBC = \angle XDA.$ Prove that $\angle BXA + \angle DXC = 180^{\circ}$

Solution

2018 IMO 6.png

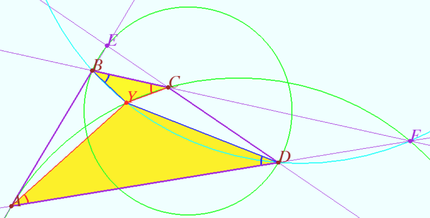
Special case

We construct point $X_0$ and prove that $X_0$ coincides with the point $X.$

Let $AD = CD$ and $AB = BC \implies AB \cdot CD = BC \cdot DA.$

Let $E$ and $F$ be the intersection points of $AB$ and $CD,$ and $BC$ and $DA,$ respectively.

The points $B$ and $D$ are symmetric with respect to the circle $\omega = ACEF$ (Claim 1).

The circle $\Omega = FBD$ is orthogonal to the circle $\omega$ (Claim 2).

Let $X_0$ be the point of intersection of the circles $\omega$ and $\Omega.$ Quadrilateral $AX_0CF$ is cyclic $\implies$ \[\angle X_0AB = \frac {\overset{\Large\frown} {X_0CE}}{2} = \frac {360^\circ -\overset{\Large\frown} {X_0AFE}}{2} = 180^\circ - \angle X_0CE = \angle X_0CD.\]

Similarly, quadrangle $DX_0BF$ is cyclic $\implies \angle X_0BC = \angle X_0DA$.

This means that point $X_0$ coincides with the point $X$.

$\hspace{10mm} \angle FCX = \angle BCX = \frac {\overset{\Large\frown} {XAF}}{2}$ of $\omega.$

$\hspace{10mm} \angle CBX = \angle XDA = \frac {\overset{\Large\frown} {XBF}}{2}$ of $\Omega.$

The sum $\overset{\Large\frown} {XAF} + \overset{\Large\frown} {XBF} = 180^\circ$ (Claim 3) $\implies$

$\angle XCB + \angle XBC = 90^\circ \implies \angle CXB = 90^\circ.$

Similarly, $\angle AXD = 90^\circ \implies \angle BXA + \angle DXC = 360^\circ -\angle AXD -\angle CXB = 180^\circ.$

2018 IMO 6a.png
2018 IMO 6bb.png
2018 IMO 6c.png
2018 IMO 6d.png

Common case

Denote by $O$ the intersection point of the perpendicular bisector of $AC$ and $BD.$ Let $\omega$ be a circle (red) with center $O$ and radius $OA.$

The points $B$ and $D$ are symmetric with respect to the circle $\omega$ (Claim 1).

The circles $BDF$ and $BDE$ are orthogonal to the circle $\omega$ (Claim 2).

Circles $ACF$ and $ACE$ are symmetric with respect to the circle $\omega$ (Lemma).

Denote by $X_0$ the point of intersection of the circles $BDF$ and $ACE.$ Quadrangle $BX_0DF$ is cyclic $\implies \angle X_0BC = \angle X_0DA$ (see Special case). Similarly, quadrangle $AX_0CE$ is cyclic $\implies \angle X_0AB = \angle X_0CD = \alpha.$

The required point $X = X_0$ is constructed.

Denote by $Y$ the point of intersection of circles $BDF$ and $ACF.$

Quadrangle $BYDF$ is cyclic $\implies \angle CBY = \angle ADY.$

Quadrangle $AYCF$ is cyclic $\implies \angle YAD = \angle BCY.$

The triangles $\triangle YAD \sim \triangle YCB$ by two angles, so \[\frac {BC}{AD} = \frac {CY}{AY} = \frac {BY} {DY} \hspace{10mm} (1).\]

The points $X$ and $Y$ are symmetric with respect to the circle $\omega$, since they lie on the intersection of the circles $ACF$ and $ACE$ symmetric with respect to $\omega$ and the circle $BDF$ orthogonal to $\omega.$

The point $C$ is symmetric to itself, the point $X$ is symmetric to $Y$ with respect to $\omega \implies \frac{CX}{CY} = \frac {R^2}{OC \cdot OY} , \frac {AX}{AY} = \frac {R^2}{OA \cdot OY}.$ Usung $(1)$ and the equality $OA = OC,$ we get \[\frac{CY}{AY} = \frac {CX}{AX} = \frac{BC}{AD}.\] The point $C$ is symmetric to itself, the point $B$ is symmetric to $D$ with respect to $\omega \implies$ \[\triangle OBC \sim \triangle OCD \implies \frac {OB}{OC} = \frac {BC}{CD} = \frac {OC}{OD},\] \[\frac {OB}{OD} = \frac {OB}{OC} \cdot \frac {OC}{OD} = \frac{BC^2}{CD^2} = \frac{BC}{CD} \cdot \frac {AB}{AD}.\] The point $B$ is symmetric to $D$ and the point $X$ is symmetric to $Y$ with respect to $\omega,$ hence \[\frac {BX}{DY} = \frac {R^2}{OD \cdot OY} ,\frac {DX}{BY} = \frac{R^2}{OB \cdot OY}.\] \[\frac{BX}{DX} =\frac{DY}{BY} \cdot \frac {OB}{OD} = \frac{AD}{BC} \cdot \frac{BC}{CD} \cdot \frac{AB}{AD} = \frac{AB}{CD}.\] Denote $\angle XAB = \angle XCD = \alpha, \angle BXA = \varphi, \angle DXC = \psi.$

By the law of sines for $\triangle ABX,$ we obtain $\frac {AB}{\sin \varphi} = \frac{BX}{\sin \alpha}.$

By the law of sines for $\triangle CDX,$ we obtain $\frac {CD}{\sin \psi} = \frac {DX}{\sin \alpha}.$

We make transformation and get \[{\sin \psi} = \frac {CD}{DX} {\sin \alpha} = \frac{CD}{DX} \cdot {\frac{DX \cdot AB}{BX \cdot CD}} {\sin \alpha} = \frac {AB}{BX}\sin \alpha = \sin \varphi.\] If $\varphi = \psi,$ then $\triangle XAB \sim \triangle XCD \implies \frac {CD}{AB} = \frac {BX}{DX} = \frac{AX}{CX} = \frac {AD}{BC}.$ $CD \cdot BC = AB \cdot AD.$ Given that $AB \cdot CD = BC \cdot DA \implies BC \cdot (CD – AD) = AB \cdot (AD – CD)\implies AD = CD, AB = BC.$ This is a special case.

In all other cases, the equality of the sines follows $\psi = 180° – \varphi \implies \varphi + \psi = 180°.$

2018 IMO 6 Claim 3.png
2018 IMO 6a.png

Claim 1 Let $A, C,$ and $E$ be arbitrary points on a circle $\omega, l$ be the perpendicular bisector to the segment $AC.$ Then the straight lines $AE$ and $CE$ intersect $l$ at the points $B$ and $D,$ symmetric with respect to $\omega.$

Claim 2 Let points $B$ and $D$ be symmetric with respect to the circle $\omega.$ Then any circle $\Omega$ passing through these points is orthogonal to $\omega.$

Claim 3 The sum of the arcs between the points of intersection of two perpendicular circles is $180^\circ.$ In the figure they are a blue and red arcs $\overset{\Large\frown} {CD}, \alpha + \beta = 180^\circ.$

Lemma The opposite sides of the quadrilateral $ABCD$ intersect at points $E$ and $F$ ($E$ lies on $AB$). The circle $\omega$ centered at the point $O$ contains the ends of the diagonal $AC.$ The points $B$ and $D$ are symmetric with respect to the circle $\omega$ (in other words, the inversion with respect to $\omega$ maps $B$ into $D).$ Then the circles $ACE$ and $ACF$ are symmetric with respect to $\omega.$ Proof We will prove that the point $G,$ symmetric to the point $E$ with respect to $\omega,$ belongs to the circle $ACF.$ For this, we will prove the equality $\angle AGC = \angle AFC.$

A circle $BDE$ containing points $B$ and $D$ symmetric with respect to $\omega,$ is orthogonal to $\omega$ (Claim 2) and maps into itself under inversion with respect to the circle $\omega.$ Hence, the point $E$ under this inversion passes to some point $G,$ of the same circle $BDE.$

A straight line $ABE$ containing the point $A$ of the circle $\omega,$ under inversion with respect to $\omega,$ maps into the circle $OADG.$ Hence, the inscribed angles of this circle are equal $\angle ADB = \angle AGE.$ $\angle OCE = \angle CGE (CE$ maps into $CG)$ and $\angle OCE = \angle BCD (BC$ maps into $DC).$ Consequently, the angles $\angle AFC = \angle ADB – \angle FBD = \angle AGE -$\angle CGE = $\angle AGC.$ These angles subtend the $\overset{\Large\frown} {AC}$ of the $ACF$ circle, that is, the point $G,$ symmetric to the point $E$ with respect to $\omega,$ belongs to the circle $ACF.$

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2018_IMO_Problems/Problem_6&oldid=177220"