Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus
During AMC testing, the AoPS Wiki is in read-only mode and no edits can be made.

Difference between revisions of "Symmedians, Lemoine point"

(→‎Common Lemoine point)
(→‎Lemoine point properties)
Line 95: Line 95:
  
 
'''vladimir.shelomovskii@gmail.com, vvsss'''
 
'''vladimir.shelomovskii@gmail.com, vvsss'''
 +
==Parallel lines==
 +
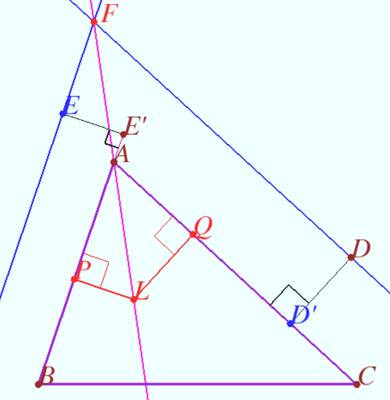
[[File:Symmedians perp and par.png|390px|right]]
 +
Let <math>\triangle ABC</math> and it’s Lemoine point <math>L</math> be given.
 +
 +
Let <math>D</math> be an arbitrary point. Let <math>D'</math> be the foot from <math>D</math> to line <math>\overline{AC}</math>.
 +
 +
Denote <math>\ell</math> the line through <math>D</math> and parallel to <math>AC.</math>
 +
 +
Denote <math>\ell'</math> the line parallel to <math>AB</math> such that distance <math>EE' = DD' \cdot \frac {AB}{AC}</math> and points <math>E</math> and <math>D</math> are both in the exterior (interior) of <math>\triangle ABC.</math>
 +
 +
Prove that points <math>F = \ell \cap \ell', A,</math> and <math>L</math> are collinear.
 +
 +
<i><b>Proof</b></i>
 +
 +
Denote <math>P(Q)</math> the foot from <math>L</math> to <math>\overline{AB}(\overline{AC})</math>.
 +
 +
<cmath>\frac {PL}{AB} = \frac {QL}{AC} \implies \frac {PL}{EE'} = \frac {QL}{DD'}.</cmath>
 +
Denote <math>F = AL \cap \ell, F' = AL \cap \ell' \implies</math>
 +
<cmath>\frac {FA}{AL} = \frac {DD'}{QL} =  \frac {EE'}{PL} =  \frac {F'A}{AL} \implies F = F'.</cmath>
 +
 +
<i><b>Corollary</b></i>
 +
 +
If squares <math>ABGF</math> and <math>ACDE</math> are constructed in the exterior of <math>\triangle ABC,</math> then <math>AO,</math> where <math>O</math> is the center of circle <math>\odot AEF,</math> is the symmedian in <math>\triangle ABC</math> through <math>A.</math>
 +
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''
 +
 
==Common Lemoine point==
 
==Common Lemoine point==
 
[[File:L to L.png|440px|right]]
 
[[File:L to L.png|440px|right]]

Revision as of 14:58, 31 July 2024

The reflecting of the median over the corresponding angle bisector is the symmedian. The angle formed by the symmedian and the angle bisector has the same measure as the angle between the median and the angle bisector, but it is on the other side of the angle bisector. The symmedian $AS_A$ is isogonally conjugate to the median $AM_A.$

There are three symmedians. They are meet at a triangle center called the Lemoine point.

Proportions

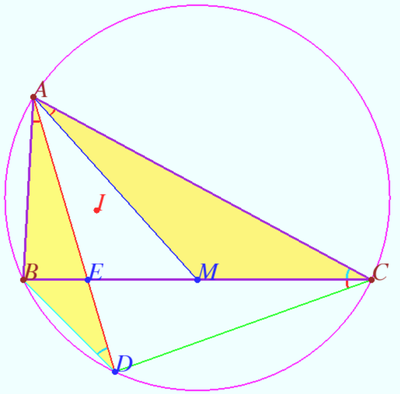
Symedian segments.png

Let $\triangle ABC$ be given.

Let $AM$ be the median, $\Omega = \odot ABC, E \in BC, D = AE \cap \Omega \ne A.$

Prove that iff $AE$ is the symmedian than $\frac {BD}{CD} = \frac{AB}{AC}, \frac {BE}{CE} = \left (\frac{AB}{AC} \right )^2.$

Proof

1. Let $AE$ be the symmedian. So $\angle BAD = \angle CAM.$ \[\angle BDA = \angle ACB = \angle ACM \implies \triangle ABD \sim \triangle AMC \implies\] \[\frac {AM}{MC}= \frac {AB}{BD}.\] Similarly $\triangle ABM \sim \triangle ADC \implies \frac {AM}{MB}= \frac {AC}{CD}.$ \[BM = MC \implies \frac {BD}{CD} = \frac{AB}{AC}.\]

By applying the Law of Sines we get \[\frac{AB}{\sin \angle AEB} = \frac{BE}{\sin \angle BAD}, \frac{CD}{\sin \angle CED} = \frac{CE}{\sin \angle CDE},\] \[\frac{AC}{\sin \angle ADC} = \frac{BD}{\sin \angle BAD} \implies \frac {BE}{CE} = \frac{AB}{CD} \cdot \frac {BD}{AC} = \frac{AB^2}{AC^2}.\] Similarly, $\frac {AE}{ED} = \frac{AB^2}{BD^2}.$

2. $\frac {BD}{CD} = \frac{AB}{AC}.$

As point $D$ moves along the fixed arc $BC$ from $B$ to $C$, the function $F(D) = \frac {BD}{CD}$ monotonically increases from zero to infinity. This means that there is exactly one point at which the condition is satisfied. In this case, point $D$ lies on the symmedian.

Similarly for point $E.$

Corollary

Let $AE$ be the $A-$ symmedian of $\triangle ABC.$

Then $BE$ is the $B-$ symmedian of $\triangle ABD, CE$ is the $C-$ symmedian of $\triangle ACD, DE$ is the $D-$ symmedian of $\triangle BCD.$

vladimir.shelomovskii@gmail.com, vvsss

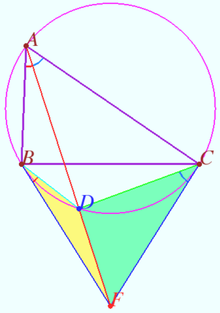
Symmedian and tangents

Tangents and symmedian.png

Let $\triangle ABC$ and it’s circumcircle $\Omega$ be given.

Tangents to $\Omega$ at points $B$ and $C$ intersect at point $F.$

Prove that $AF$ is $A-$ symmedian of $\triangle ABC.$

Proof

Denote $D = AF \cap \Omega \ne A.$ WLOG, $\angle BAC < 180^\circ.$ \[\triangle FDB \sim \triangle FBA \implies \frac {BD}{AB} = \frac{DF}{BF}.\] \[\triangle FDC \sim \triangle FCA \implies \frac {CD}{AC} = \frac{DF}{CF}.\] $BF = CF \implies \frac {BD}{CD} = \frac{AB}{AC} \implies AD$ is $A-$ symmedian of $\triangle ABC.$

Corollary

Tangents to symmedian.png

Let $\triangle ABC$ and it’s circumcircle $\Omega$ be given.

Let tangent to $\Omega$ at points $A$ intersect line $BC$ at point $F.$

Let $FD$ be the tangent to $\Omega$ different from $FA.$

Then $AD$ is $A-$ symmedian of $\triangle ABC.$

vladimir.shelomovskii@gmail.com, vvsss

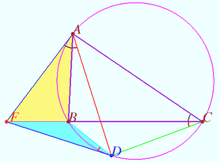
Lemoine point properties

L and G.png

Let $\triangle ABC$ be given. Let $L$ be the Lemoine point of $\triangle ABC.$

\[LD \perp BC, D \in BC, LE \perp AC, E \in AC, LF \perp AB, F \in AB.\]

Prove that $\frac{LD}{BC} = \frac{LE}{AC} = \frac{LF}{AB}, L$ is the centroid of $\triangle DEF.$

Proof

Let $G$ be the centroid of $\triangle ABC, GD' \perp BC, D' \in BC,$ \[LE' \perp AC, E' \in AC, LF' \perp AB, F' \in AB.\]

The double area of $\triangle AGC$ is $2[AGC] = GE' \cdot AC = 2[BGC] = GD' \cdot BC \implies \frac {GD' }{GE' } = \frac {AC}{BC}.$

Point $L$is the isogonal conjugate of point $G$ with respect to $\triangle ABC \implies \frac {LE}{LD} =\frac {GD' }{GE' } =\frac {AC}{BC}.$

Similarly, one can get $\frac {LE}{AC} = \frac {LD}{BC} = \frac {LF}{AB} = k.$

The double area of $\triangle DLE$ is $2[DLE] = LD \cdot LE \sin \angle DLE = k BC \cdot k AC \cdot \sin \angle ACB = k^2 \cdot 2[ABC].$

Similarly, one can get $[DLE] = [DLF] = [DEF] = k^2 [ABC] \implies L$ is the centroid of $\triangle DEF.$

Corollary

Vector sum $\vec {LE} + \vec {LD} + \vec {LF} = \vec 0.$

Each of these vectors is obtained from the triangle side vectors by rotating by $90^\circ$ and multiplying by a constant $k^2,$ \[\vec {AC} + \vec {CB} + \vec {BA} = \vec 0.\]

vladimir.shelomovskii@gmail.com, vvsss

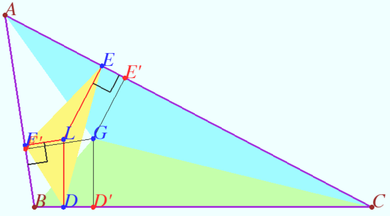
Parallel lines

Symmedians perp and par.png

Let $\triangle ABC$ and it’s Lemoine point $L$ be given.

Let $D$ be an arbitrary point. Let $D'$ be the foot from $D$ to line $\overline{AC}$.

Denote $\ell$ the line through $D$ and parallel to $AC.$

Denote $\ell'$ the line parallel to $AB$ such that distance $EE' = DD' \cdot \frac {AB}{AC}$ and points $E$ and $D$ are both in the exterior (interior) of $\triangle ABC.$

Prove that points $F = \ell \cap \ell', A,$ and $L$ are collinear.

Proof

Denote $P(Q)$ the foot from $L$ to $\overline{AB}(\overline{AC})$.

\[\frac {PL}{AB} = \frac {QL}{AC} \implies \frac {PL}{EE'} = \frac {QL}{DD'}.\] Denote $F = AL \cap \ell, F' = AL \cap \ell' \implies$ \[\frac {FA}{AL} = \frac {DD'}{QL} = \frac {EE'}{PL} = \frac {F'A}{AL} \implies F = F'.\]

Corollary

If squares $ABGF$ and $ACDE$ are constructed in the exterior of $\triangle ABC,$ then $AO,$ where $O$ is the center of circle $\odot AEF,$ is the symmedian in $\triangle ABC$ through $A.$

vladimir.shelomovskii@gmail.com, vvsss

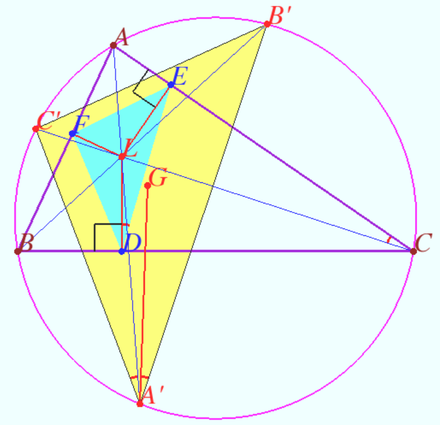
Common Lemoine point

L to L.png
2 46 Prasolov.png

Let $\triangle ABC$ be given, $\Omega = \odot ABC.$

Let $L$ be the Lemoine point of $\triangle ABC.$

$A' = AL \cap \Omega \ne A, B' = BL \cap \Omega \ne B, C' = CL \cap \Omega \ne C.$

Prove that the point $L$ is the Lemoine point of $\triangle A'B'C'.$

Proof

Denote point $D$ so that $LD \perp BC, D \in BC.$

Similarly denote $E \in AC$ and $F \in AB.$ $L$ is the centroid of $\triangle DEF.$

$\triangle DEF \sim \triangle A'B'C'$ (see Claim).

Let point $G$ be the centroid of $\triangle A'B'C' \implies$ \[\angle LDE = \angle GA'B'.\] $CDLE$ is cyclic so $\angle LDE = \angle LCE = \angle LCA = \angle C'CA = \angle C'A'A = \angle C'A'L$ therefore $A'L$ and $A'G$ are isogonals with respect $\angle C'A'B'.$

Similarly $B'L$ and $B'G$ are isogonals with respect $\angle A'B'C' \implies$

$L$ is the isogonal conjugate of a point $G$ with respect to a triangle $\triangle A'B'C'$

so $L$ is the Lemoine point of $\triangle A'B'C'.$

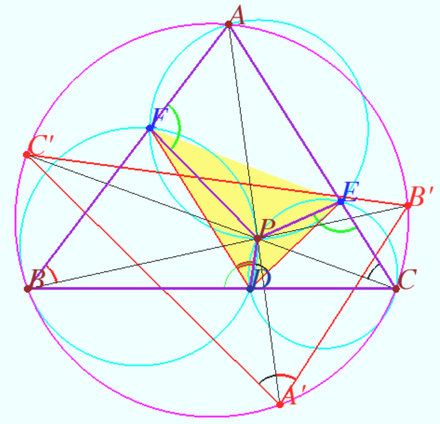
Claim

Lines AP, BP and CP intersect the circumcircle of $\triangle ABC$ at points $A', B',$ and $C'.$

Points $D, E,$ and $F$ are taken on the lines $BC, CA,$ and $AB$ so that $\angle PDB = \angle PFA = \angle PEC$ (see diagram).

Prove that $\triangle A'B'C' \sim \triangle DEF.$

Proof

$\angle PFA = \angle PDB \implies PDBF$ is cyclic so $\angle PDF = \angle PBF = \angle ABB' = \angle AA'B'.$

Similarly, $\angle PDE = \angle AA'C' \implies$ $\angle FDE = \angle PDF + \angle PDE = \angle AA'B' + \angle AA'C' = \angle B'A'C'.$

Similarly, $\angle DEF = \angle A'B'C'. \blacksquare$

vladimir.shelomovskii@gmail.com, vvsss

Lemoine point extreme properties

Lemoine point $L$ minimizes the sum of the squares of the distances to the sides of the triangle (among all points internal to $\triangle ABC.)$

Proof

Let us denote the desired point by $X.$ Let us imagine that point $X$ is connected to springs of equal stiffness attached to the sides at points $D, E,$ and $F$ and contacts sliding along them without friction. The segments modeling the springs will be perpendicular to the corresponding side. The energy of each spring is proportional to the square of its length. The minimum energy of the system corresponds to the minimum of the sum of the squares of the lengths of these segments, that is, the sum of the squares of the distances from $X$ to the sides.

It is known that the minimum spring energy corresponds to the equilibrium position. The condition of equilibrium at a point $X$ is the equality to zero of the vector sum of forces applied from the springs to the point $X.$ The force developed by each spring is proportional to its length, that is, the equilibrium condition is that the sum of the vectors $\vec {XE} + \vec {XD} + \vec {XF} = \vec 0.$ It is clear that the point $L$ corresponds to this condition.

vladimir.shelomovskii@gmail.com, vvsss

Lemoine point and perpendicularity

Symmedians perp.png

Let $\triangle ABC$ be given. Let $L$ be the Lemoine point of $\triangle ABC,$ $LD \perp BC, D \in BC, LE \perp AC, E \in AC, LF \perp AB, F \in AB.$

$M$ is the midpoint $BC.$

Prove that $FE \perp AM.$

Proof

$AL$ is isogonal conjugated $AM$ with respect $\angle A \implies \angle BAL = \angle CAM.$

$LE \perp AE, LF \perp AF \implies AELD$ is cyclic.

$\angle CAM = \angle BAL = \angle FEL.$

$LE \perp AC \implies EF \perp AM.$

vladimir.shelomovskii@gmail.com, vvsss

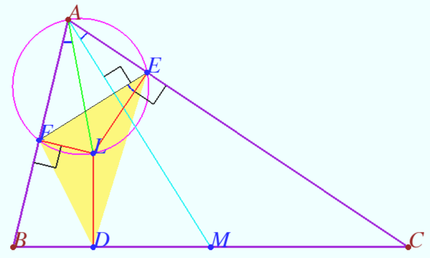
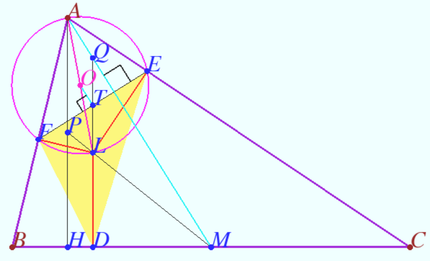
Lemoine point line

L M P line.png

Let $\triangle ABC$ be given. Let $L$ be the Lemoine point of $\triangle ABC.$

Let $AH$ be the height, $AM$ be the median, $LD \perp BC, D \in BC,$

$LE \perp AC, E \in AC, LF \perp AB, F \in AB, P$ be the midpoint $AH$.

Prove that the points $L, P,$ and $M$ are collinear.

Proof

Denote $O$ the circumcenter $\odot AELF, LO = AO.$

Denote $T$ the midpoint $FE \implies OT \perp FE.$

$L$ is centroid of $\triangle DEF \implies DLT$ is $D-$median of $\triangle DEF.$

Denote $Q$ the point symmetric $L$ with respect $T \implies QT$ is the midline of $\triangle LAQ \implies AQ \perp EF \implies Q \in AM \perp EF.$

$LD = 2 TL \implies DL = LQ \implies ML$ is the median of $\triangle MDQ.$

$MP$ is the median of $\triangle MHA, HA || DQ \implies$ the points $L, P,$ and $M$ are collinear.

vladimir.shelomovskii@gmail.com, vvsss

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Symmedians,_Lemoine_point&oldid=224066"