Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "1972 IMO Problems/Problem 2"
Line 53: Line 53:
 
Before giving the missing details, let us remember that a quadrilateral
 
Before giving the missing details, let us remember that a quadrilateral
 
<math>ABCD</math> is inscribable if and only if a pair of opposing angles adds
 
<math>ABCD</math> is inscribable if and only if a pair of opposing angles adds
−
up to <math>\pi</math>, in other words <math>\angle A + \angle C = \pi</math>, or equivalently,
+
up to <math>\pi,</math> in other words <math>\angle A + \angle C = \pi,</math> or equivalently,
 
<math>\angle B + \angle D = \pi</math>.  In particular, any isosceles trapezoid is
 
<math>\angle B + \angle D = \pi</math>.  In particular, any isosceles trapezoid is
 
inscribable.
 
inscribable.
Line 74: Line 74:
 
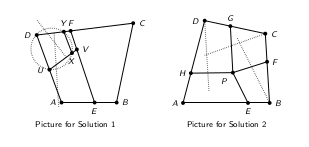
Let us now make precise what it means that <math>U</math> should be close enough
 
Let us now make precise what it means that <math>U</math> should be close enough
 
to <math>D</math>, or <math>V</math> should be close enough to <math>F</math>, so that we can find <math>XY</math>,
 
to <math>D</math>, or <math>V</math> should be close enough to <math>F</math>, so that we can find <math>XY</math>,
−
so that <math>XYFV</math> is inscribable.
+
so that <math>DUX</math> is inscribable.
  
 +
One way of constructing the circle <math>DUXY</math> is the following: Let us consider
 +
the median of <math>DF</math>.  If <math>\angle D</math> is acute, it intersects <math>DA</math> someplace
 +
on the same side as <math>A</math> of <math>DA</math> (relative to <math>D</math>).  Let us pick <math>U</math> between
 +
<math>D</math> and this point of intersection (this is the first condition for <math>U</math>
 +
being close enough to <math>D</math>).  Note that <math>VU</math> is of fixed slope and length
 +
because <math>UVEA</math> has to be an isosceles trapezoid.  We pick <math>Y</math> between <math>D</math>
 +
and <math>F</math>,  Then the median of <math>DY</math> is on the same side as <math>D</math> of the median
 +
of <math>DF</math>.  The center <math>O</math> of the circle we are looking for is at the
 +
intersection of the median to <math>DY</math> and the median to <math>DU</math>.  The circle
 +
with this center <math>O</math> and radius <math>OD = OU = OY</math> intersects <math>UV</math> in a point
 +
<math>X</math>.  We need to make sure that <math>X</math> is between <math>U</math> and <math>V</math>.  For this,
 +
we need to know that <math>O</math> is on the same side of the median to <math>UV</math> as <math>D</math>
 +
and <math>U</math>.  If we denote <math>Z</math> the intersection of the median to <math>UV</math> with <math>UD</math>,
 +
we need to know that <math>UZ > UD/2</math>.  We have
 +
<math>UZ = (UV/2) \cdot (1/\cos (\angle DUV))</math>, so the condition becomes
 +
<math>UV/(2 /\cos (\angle DUV)) > UD/2</math>.  Since <math>UV</math> and <math>\angle DUV</math> are of
 +
specified sizes, this gives a second condition for <math>UD</math> being small enough.
  
 +
In the discussion above, we assumed <math>\angle D</math> acute and implicitly, we
 +
assumed <math>\angle DUV</math> acute.  The cases when either of these angles is not
 +
acute is less restrictive, and the arguments for choosing <math>U</math>, and then
 +
<math>Y</math> are similar (and easier).  We will skip the discussion for these cases.
  
 +
 +
==Solution 2==
  
  

Revision as of 02:05, 27 March 2025

Problem

Prove that if $n \geq 4$, every quadrilateral that can be inscribed in a circle can be dissected into $n$ quadrilaterals each of which is inscribable in a circle.

Solution

Our initial quadrilateral will be $ABCD$.

For $n=4$, we do this:

Take $E\in AB,F\in CD,\ EF\|AD$ with $E,F$ sufficiently close to $A,D$ respectively. Take $U\in AD,V\in EF$ such that $AEVU$ is an isosceles trapezoid, with $V$ close enough to $F$ (or $U$ close enough to $D$) that we can find a circle passing through $U,D$ (or $F,V$) which cuts the segments $UV,DF$ in $X,Y$. Our four cyclic quadrilaterals are $BCFE,\ AEVU,\ VFYX,\ YXUD$.

For $n\ge 5$ we do the exact same thing as above, but now, since we have an isosceles trapezoid, we can add as many trapezoids as we want by dissecting the one trapezoid with lines parallel to its bases.

The above solution was posted and copyrighted by grobber. The original thread for this problem can be found here: [1]


Remarks (added by pf02, March 2025)

The construction described in the solution above is correct (in the sense that it describes a legitimate way of dissecting an inscribable quadrilateral into four inscribable quadrilaterals). However, the solution is incomplete and sloppily written.

Below I will discuss and complete the solution given above. Then, I will give a second solution. And finally, I will discuss the cases when $n = 2, n = 3$.


Discussion and completion of the above solution

The first issue is the fact that a construction is described, but there is no proof, not even a hint, why the the quadrilaterals are inscribable. This is not obvious, and it needs a proof. I will give the proof below.

The second issue is the vagueness of "close enough" used twice in the proof. The first time it is used, "$E, F$ sufficiently close to $A, D$ respectively" is not needed (indeed, and segment $EF$ parallel to $AD$ would do), so there is no need to make this more precise. The second time it is used, namely "$V$ close enough to $F$ (or $U$ close enough to $D$) that we can find a circle passing through $U, D$ (or $F, V$)" is indeed needed, and it is not at all clear what "close enough" should be, or that this is at all possible. I will come back to this shortly.

The third issue is poor wording. We don't need to "add as many trapezoids as we want". We want to dissect the one isosceles trapezoid into as many isosceles trapezoids as we want by lines parallel to its bases.

Prob 1972 2.png

Before giving the missing details, let us remember that a quadrilateral $ABCD$ is inscribable if and only if a pair of opposing angles adds up to $\pi,$ in other words $\angle A + \angle C = \pi,$ or equivalently, $\angle B + \angle D = \pi$. In particular, any isosceles trapezoid is inscribable.

Now let us show that the four quadrilaterals are inscribable. It is easy to see that the first one, $EBCF$ is inscribable. Indeed, $\angle C + \angle A = \pi$. We know that $\angle A = \angle FEB$ because of parallelism, so $\angle C + \angle FEB = \pi$. The second one, $AEVU$ is an isosceles trapezoid by the choice of $VU$, so it is inscribable. The third one, $DUXY$ is inscribable by construction. It remains to be shown that $XYFV$ is inscribable.

We have $\angle YFV = \pi - \angle CFE = \angle B = \pi - \angle D = \angle YXU = \pi - \angle YXV$. This shows that $XYFV$ is inscribable.

Note that as suggested by the solution, we could have chosen $XY$ so that $XYFV$ is inscribable, in which case a similar argument would have shown that $DUXY$ is inscribable as well.

Let us now make precise what it means that $U$ should be close enough to $D$, or $V$ should be close enough to $F$, so that we can find $XY$, so that $DUX$ is inscribable.

One way of constructing the circle $DUXY$ is the following: Let us consider the median of $DF$. If $\angle D$ is acute, it intersects $DA$ someplace on the same side as $A$ of $DA$ (relative to $D$). Let us pick $U$ between $D$ and this point of intersection (this is the first condition for $U$ being close enough to $D$). Note that $VU$ is of fixed slope and length because $UVEA$ has to be an isosceles trapezoid. We pick $Y$ between $D$ and $F$, Then the median of $DY$ is on the same side as $D$ of the median of $DF$. The center $O$ of the circle we are looking for is at the intersection of the median to $DY$ and the median to $DU$. The circle with this center $O$ and radius $OD = OU = OY$ intersects $UV$ in a point $X$. We need to make sure that $X$ is between $U$ and $V$. For this, we need to know that $O$ is on the same side of the median to $UV$ as $D$ and $U$. If we denote $Z$ the intersection of the median to $UV$ with $UD$, we need to know that $UZ > UD/2$. We have $UZ = (UV/2) \cdot (1/\cos (\angle DUV))$, so the condition becomes $UV/(2 /\cos (\angle DUV)) > UD/2$. Since $UV$ and $\angle DUV$ are of specified sizes, this gives a second condition for $UD$ being small enough.

In the discussion above, we assumed $\angle D$ acute and implicitly, we assumed $\angle DUV$ acute. The cases when either of these angles is not acute is less restrictive, and the arguments for choosing $U$, and then $Y$ are similar (and easier). We will skip the discussion for these cases.


Solution 2

TO BE CONTINUED. SAVING MID WAY, SO I DON'T LOOSE WORK DONE SO FAR.


See Also

1972 IMO (Problems) • Resources
Preceded by
Problem 1 		1 • 2 • 3 • 4 • 5 • 6 Followed by
Problem 3
All IMO Problems and Solutions
Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=1972_IMO_Problems/Problem_2&oldid=246126"