Difference between revisions of "2022 AIME I Problems/Problem 14"

Latest revision as of 04:07, 4 May 2025

Problem

Given $\triangle ABC$ and a point $P$ on one of its sides, call line $\ell$ the $\textit{splitting line}$ of $\triangle ABC$ through $P$ if $\ell$ passes through $P$ and divides $\triangle ABC$ into two polygons of equal perimeter. Let $\triangle ABC$ be a triangle where $BC = 219$ and $AB$ and $AC$ are positive integers. Let $M$ and $N$ be the midpoints of $\overline{AB}$ and $\overline{AC},$ respectively, and suppose that the splitting lines of $\triangle ABC$ through $M$ and $N$ intersect at $30^\circ.$ Find the perimeter of $\triangle ABC.$

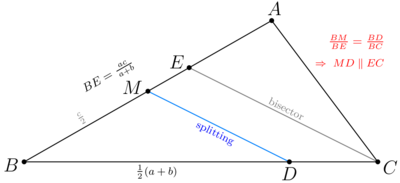
The Geometry Part - Solution 1

Consider the splitting line through $M$ . Extend $D$ on ray $BC$ such that $CD=CA$ . Then the splitting line bisects segment $BD$ , so in particular it is the midline of triangle $ABD$ and thus it is parallel to $AD$ . But since triangle $ACD$ is isosceles, we can easily see $AD$ is parallel to the angle bisector of $C$ , so the splitting line is also parallel to this bisector, and similar for the splitting line through $N$ . Some simple angle chasing reveals the condition is now equivalent to $\angle A=120^\circ$ .

- MortemEtInteritum

The Geometry Part - Solution 2

Let $PM$ and $QN$ be the splitting lines. Reflect $B$ across $Q$ to be $B'$ and $C$ across $P$ to be $C'$ . Take $S_B$ and $S_C$ , which are spiral similarity centers on the other side of $BC$ as $A$ such that $\triangle S_BB'C \sim \triangle S_BBA$ and $\triangle S_CC'B \sim \triangle S_CCA$ . This gets that because $\angle S_BCB = \angle S_BCB' = \angle S_BAB$ and $\angle S_CBC = \angle S_CBC' = \angle S_CAC$ , then $S_B$ and $S_C$ are on $\triangle ABC$ 's circumcircle. Now, we know that $\triangle S_BBB' \sim \triangle S_BAC$ and $\triangle S_CCC' \sim \triangle S_CAB$ so because $BA=B'C$ and $CA=C'B$ , then $S_BB=SBB'$ and $S_CC=S_CC'$ and $S_BQ \perp BC$ and $S_CP \perp BC$ .

We also notice that because $Q$ and $N$ correspond on $\triangle S_BBB'$ and $\triangle S_BAC$ , and because $P$ and $M$ correspond on $\triangle S_CCC'$ and $\triangle S_CAB$ , then the angle formed by $NQ$ and $BA$ is equal to the angle formed by $B'C$ and $NQ$ which is equal to $\angle BS_BQ = \angle QS_BB'$ . Thus, $\angle CBA=2\angle CQN$ . Similarly, $\angle BCA = 2\angle QPM$ and so $\angle CBA + \angle BCA = 2\angle PQN + 2\angle QPM = 60^{\circ}$ and $\angle A = 120^{\circ}$ .

- kevinmathz

The NT Part

We now need to solve $a^2+ab+b^2 = 3^2\cdot 73^2$ . A quick $(\bmod 9)$ check gives that $3\mid a$ and $3\mid b$ . Thus, it's equivalent to solve $x^2+xy+y^2 = 73^2$ .

Let $\omega$ be one root of $\omega^2+\omega+1=0$ . Then, recall that $\mathbb Z[\omega]$ is the ring of integers of $\mathbb Q[\sqrt{-3}]$ and is a unique factorization domain. Notice that $N(x-y\omega) = (x-y\omega)(x-y\omega^2) = x^2+xy+y^2$ . Therefore, it suffices to find an element of $\mathbb Z[\omega]$ with the norm $73^2$ .

To do so, we factor $73$ in $\mathbb Z[\omega]$ . Since it's $1\pmod 3$ , it must split. A quick inspection gives $73 = (8-\omega)(8-\omega^2)$ . Thus, $N(8-\omega) = 73$ , so $\begin{align*} 73^2 &= N((8-\omega)^2) \\ &= N(64 - 16\omega + \omega^2) \\ &= N(64 - 16\omega + (-1-\omega)) \\ &= N(63 - 17\omega), \end{align*}$ giving the solution $x=63$ and $y=17$ , yielding $a=189$ and $b=51$ , so the sum is $\boxed{459}$ . Since $8-\omega$ and $8-\omega^2$ are primes in $\mathbb Z[\omega]$ , the solution must divide $73^2$ . One can then easily check that this is the unique solution.

- MarkBcc168

Solution (Geometry + Number Theory)

Denote $BC = a$ , $CA = b$ , $AB = c$ .

Let the splitting line of $\triangle ABC$ through $M$ (resp. $N$ ) crosses $\triangle ABC$ at another point $X$ (resp. $Y$ ).

WLOG, we assume $c \leq b$ .

$\textbf{Case 1}$ : $a \leq c \leq b$ .

We extend segment $AB$ to $D$ , such that $BD = a$ . We extend segment $AC$ to $E$ , such that $CE = a$ .

In this case, $X$ is the midpoint of $AE$ , and $Y$ is the midpoint of $AD$ .

Because $M$ and $X$ are the midpoints of $AB$ and $AE$ , respectively, $MX \parallel BE$ . Because $N$ and $Y$ are the midpoints of $AC$ and $AD$ , respectively, $NY \parallel CD$ .

Because $CB = CE$ , $\angle CBE =\angle CEB = \frac{\angle ACB}{2}$ . Because $BC = BD$ , $\angle BCD = \angle BDC = \frac{\angle ABC}{2}$ .

Let $BE$ and $CD$ intersect at $O$ . Because $MX \parallel BE$ and $NY \parallel CD$ , the angle formed between lines $MX$ and $NY$ is congruent to $\angle BOD$ . Hence, $\angle BOD = 30^\circ$ or $150^\circ$ .

We have $\begin{align*} \angle BOD & = \angle CBE + \angle BCD \\ & = \frac{\angle ACB}{2} + \frac{\angle ABC}{2} \\ & = 90^\circ - \frac{\angle A}{2} . \end{align*}$

Hence, we must have $\angle BOD = 30^\circ$ , not $150^\circ$ . Hence, $\angle A = 120^\circ$ .

This implies $a > b$ and $a >c$ . This contradicts the condition specified for this case.

Therefore, this case is infeasible.

$\textbf{Case 2}$ : $c \leq a \leq b$ .

We extend segment $CB$ to $D$ , such that $BD = c$ . We extend segment $AC$ to $E$ , such that $CE = a$ .

In this case, $X$ is the midpoint of $AE$ , and $Y$ is the midpoint of $CD$ .

Because $M$ and $X$ are the midpoints of $AB$ and $AE$ , respectively, $MX \parallel BE$ . Because $N$ and $Y$ are the midpoints of $AC$ and $CD$ , respectively, $NY \parallel AD$ .

Because $CB = CE$ , $\angle CBE =\angle CEB = \frac{\angle ACB}{2}$ . Because $BA = BD$ , $\angle BAD = \angle BDA = \frac{\angle ABC}{2}$ .

Let $O$ be a point of $AC$ , such that $BO \parallel AD$ . Hence, $\angle OBC = \angle BDA = \frac{B}{2}$ .

Because $MX \parallel BE$ and $NY \parallel AD$ and $AD \parallel BO$ , the angle formed between lines $MX$ and $NY$ is congruent to $\angle OBE$ . Hence, $\angle OBE = 30^\circ$ or $150^\circ$ .

We have $\begin{align*} \angle OBE & = \angle OBC + \angle CBE \\ & = \frac{\angle ABC}{2} + \frac{\angle ACB}{2} \\ & = 90^\circ - \frac{\angle A}{2} . \end{align*}$

Hence, we must have $\angle OBE = 30^\circ$ , not $150^\circ$ . Hence, $\angle A = 120^\circ$ .

This implies $a > b$ and $a >c$ . This contradicts the condition specified for this case.

Therefore, this case is infeasible.

$\textbf{Case 3}$ : $c \leq b \leq a$ .

We extend segment $CB$ to $D$ , such that $BD = c$ . We extend segment $BC$ to $E$ , such that $CE = b$ .

In this case, $X$ is the midpoint of $BE$ , and $Y$ is the midpoint of $CD$ .

Because $M$ and $X$ are the midpoints of $AB$ and $BE$ , respectively, $MX \parallel AE$ . Because $N$ and $Y$ are the midpoints of $AC$ and $CD$ , respectively, $NY \parallel AD$ .

Because $CA = CE$ , $\angle CAE =\angle CEB = \frac{\angle ACB}{2}$ . Because $BA = BD$ , $\angle BAD = \angle BDA = \frac{\angle ABC}{2}$ .

Because $MX \parallel AE$ and $NY \parallel AD$ , the angle formed between lines $MX$ and $NY$ is congruent to $\angle DAE$ . Hence, $\angle DAE = 30^\circ$ or $150^\circ$ .

We have $\begin{align*} \angle DAE & = \angle BAD + \angle CAE + \angle BAC \\ & = \frac{\angle ABC}{2} + \frac{\angle ACB}{2} + \angle BAC \\ & = 90^\circ + \frac{\angle BAC}{2} . \end{align*}$

Hence, we must have $\angle OBE = 150^\circ$ , not $30^\circ$ . Hence, $\angle BAC = 120^\circ$ .

In $\triangle ABC$ , by applying the law of cosines, we have $\begin{align*} a^2 & = b^2 + c^2 - 2bc \cos \angle BAC\\ & = b^2 + c^2 - 2bc \cos 120^\circ \\ & = b^2 + c^2 + bc . \end{align*}$

Because $a = 219$ , we have $b^2 + c^2 + bc = 219^2 .$

Now, we find integer solution(s) of this equation with $c \leq b$ .

Multiplying this equation by 4, we get $\left( 2 c + b \right)^2 + 3 b^2 = 438^2 . \hspace{1cm} (1)$

Denote $d = 2 c + b$ . Because $c \leq b$ , $b < d \leq 3 b$ .

Because $438^2 - 3 b^2 \equiv 0 \pmod{3}$ , $d^2 \equiv 0 \pmod{3}$ . Thus, $d \equiv 0 \pmod{3}$ . This implies $d^2 \equiv 0 \pmod{9}$ .

We also have $438^2 \equiv 0 \pmod{9}$ . Hence, $3 b^2 \equiv 0 \pmod{9}$ . This implies $b \equiv 0 \pmod{3}$ .

Denote $b = 3 p$ and $d = 3 q$ . Hence, $p < q \leq 3 p$ . Hence, Equation (1) can be written as $q^2 + 3 p^2 = 146^2 . \hspace{1cm} (2)$

Now, we solve this equation.

First, we find an upper bound of $q$ .

We have $q^2 + 3 p^2 \geq q^2 + 3 \left( \frac{q}{3} \right)^2 = \frac{4 q^2}{3}$ . Hence, $\frac{4 q^2}{3} \leq 146^2$ . Hence, $q \leq 73 \sqrt{3} < 73 \cdot 1.8 = 131.4$ . Because $q$ is an integer, we must have $q \leq 131$ .

Second, we find a lower bound of $q$ .

We have $q^2 + 3 p^2 < q^2 + 3 q^2 = 4 q^2$ . Hence, $4 q^2 > 146^2$ . Hence, $q > 73$ . Because $q$ is an integer, we must have $q \geq 74$ .

Now, we find the integer solutions of $p$ and $q$ that satisfy Equation (2) with $74 \leq q \leq 131$ .

First, modulo 9, $\begin{align*} q^2 & \equiv 146^2 - 3 p^2 \\ & \equiv 4 - 3 \cdot ( 0 \mbox{ or } 1 ) \\ & \equiv 4 \mbox{ or } 1 . \end{align*}$

Hence $q \equiv \pm 1, \pm 2 \pmod{9}$ .

Second, modulo 5, $\begin{align*} q^2 & \equiv 146^2 - 3 p^2 \\ & \equiv 1 + 2 p^2 \\ & \equiv 1 + 2 \cdot ( 0 \mbox{ or } 1 \mbox{ or } -1 ) \\ & \equiv 1 \mbox{ or } 3 \mbox{ or } - 1 . \end{align*}$

Because $q^2 \equiv 0 \mbox{ or } 1 \mbox{ or } - 1$ , we must have $q^2 \equiv 1 \mbox{ or } - 1$ . Hence, $5 \nmid q$ .

Third, modulo 7, $\begin{align*} q^2 & \equiv 146^2 - 3 p^2 \\ & \equiv 1 - 3 \cdot ( 0 \mbox{ or } 1 \mbox{ or } 5 \mbox{ or } 2 ) \\ & \equiv 1 \mbox{ or } 2 \mbox{ or } 3 \mbox{ or } 5 . \end{align*}$

Because $q^2 \equiv 0 \mbox{ or } 1 \mbox{ or } 2 \mbox{ or } 4 \pmod{ 7 }$ , we must have $q^2 \equiv 1 \mbox{ or } 2 \pmod{7}$ . Hence, $q \equiv 1, 3, 4, 6 \pmod{7}$ .

Given all conditions above, the possible $q$ are 74, 83, 88, 92, 97, 101, 106, 109, 116, 118, 127.

By testing all these numbers, we find that the only solution is $q = 97$ . This implies $p = 63$ .

Hence, $b = 3p = 189$ and $d = 3q = 291$ . Hence, $c = \frac{d - b}{2} = 51$ .

Therefore, the perimeter of $\triangle ABC$ is $b + c + a = 189 + 51 + 219 = \boxed{\textbf{(459) }}$ .

~Steven Chen (www.professorchenedu.com)

Solution (Number Theory Part)

We wish to solve the Diophantine equation $a^2+ab+b^2=3^2 \cdot 73^2$ . It can be shown that $3|a$ and $3|b$ , so we make the substitution $a=3x$ and $b=3y$ to obtain $x^2+xy+y^2=73^2$ as our new equation to solve for.

Notice that $r^2+r+1=(r-\omega)(r-{\omega}^2)$ , where $\omega=e^{i\frac{2\pi}{3}}$ . Thus, $x^2+xy+y^2 = y^2((x/y)^2+(x/y)+1) = y^2 (\frac{x}{y}-\omega)(\frac{x}{y}-{\omega}^2) = (x-y\omega)(x-y{\omega}^2).$

Note that $8^2+1^2+8 \cdot 1=73$ . Thus, $(8-\omega)(8-{\omega}^2)=73$ . Squaring both sides yields $\begin{align} (8-\omega)^2(8-{\omega}^2)^2&=73^2\\ (63-17\omega)(63-17{\omega}^2)&=73^2. \end{align}$ Thus, by $(2)$ , $(63, 17)$ is a solution to $x^2+xy+y^2=73^2$ . This implies that $a=189$ and $b=51$ , so our final answer is $189+51+219=\boxed{459}$ .

~ Leo.Euler

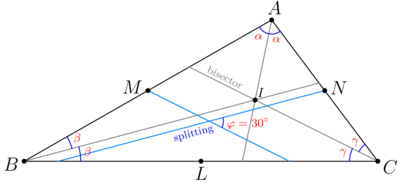
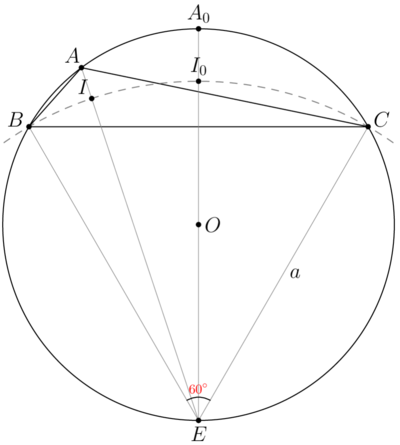
Solution(Visual geometry)

We look at upper and middle diagrams and get $\angle BAC = 120^\circ$ .

Next we use only the lower Diagram. Let $I$ be incenter $\triangle ABC$ , E be midpoint of biggest arc $\overset{\Large\frown} {BC}.$ Then bisector $AI$ cross circumcircle $\triangle ABC$ at point $E$ . Quadrilateral $ABEC$ is cyclic, so $\angle BEC = 180^\circ - \angle ABC = 60^\circ \implies BE = CE = IE = BC.$ $AE \cdot BC = AB \cdot CE + AC \cdot BE \implies AE = AB + AC$ $\implies AI +EI = AB + AC, \hspace{10mm} AI = AB+ AC – BC$ is integer. $AI = \frac {2AB \cdot AC \cdot cos \angle CAI}{AB+AC + BC} = \frac {AB \cdot AC}{AB+AC + BC} =$ $= AB + AC – BC \implies AC^2 + AB^2 + AB \cdot AC = BC^2.$ A quick $(\mod9)$ check gives that $3\mid AC$ and $3\mid AB$ . $AI \le A_0I_0 = EA_0 – EI_0 = \frac{2 BC}{\sqrt{3}} – BC = \frac {2 - \sqrt{3}}{\sqrt{3}} BC = 33.88.$ Denote $a= \frac {BC}{3}= 73, b = \frac {AC}{3}, c = \frac {AB}{3}, l = \frac {AI}{3} \le 11.$

We have equations in integers $\frac{bc}{a+b+c} = b + c – a = l \le 11.$

The solution $(b > c)$ is $b = \frac{a + l +\sqrt{a^2 – 6al – 3l^2}}{2}, c = \frac{a + l -\sqrt{a^2 – 6al – 3l^2}}{2}.$ Suppose, $a^2 – 6al – 3l^2 = (a – 3l – t)^2 \implies \frac {12l^2}{t} + t + 6l= 2a = 146.$

Now we check all possible $t = {2,3,4,6,12, ml}.$

Case $t = 2 \implies 6l^2 + 6l = 146 – 2 \implies l^2 + l = 24 \implies \O$

Case $t = 3 \implies 4l^2 + 6l = 146 – 3 = 143\implies \O.$

Case $t = 4 \implies 3l^2 + 6l = 146 – 4 =142 \implies \O.$

Case $t = 6 \implies 2l^2 + 6l = 146 – 6 = 140 \implies l = 7, b = 63, c = 17.$

Case $t = 12 \implies l^2 + 6l = 146 – 12 = 134 \implies \O.$

Case $t = ml \implies \frac{12l}{m} + 6l + ml = 146 \implies \frac{12}{m} + 6 + m = \frac{73 \cdot 2}{l}\implies \O.$

vladimir.shelomovskii@gmail.com, vvsss

Solution (The Geometry Part Using Menelaus)

Let the 2 splitting lines crossing $N$ and $M$ cross $BC$ at $G$ and $H$ . Extend $AB$ and $NG$ so that the two lines intersect at $E$ and extend $AC$ and $MH$ so that the two lines intersect at $F$ . Let $a$ , $b$ , $c$ be the corresponding side lengths for $\angle A$ , $\angle B$ , $\angle C$ . According to the question, $MH$ and $NG$ creates two sections of $\triangle ABC$ of equal perimeter, we could list out the equations:

$BG+C=a-BG$

$CH+b=a-BH$

$BG+GH+CH=a$

This results in:

$BG=\frac{a-c}{2}$

$CH=\frac{a-b}{2}$

$GH=\frac{b+c}{2}$

Now, we can apply the Menelaus Theorem to $\triangle ABC$ . Let $BE = x$ : $\frac{BE}{AE}\cdot\frac{AN}{CN}\cdot\frac{CG}{BG} = 1$ $\frac{x}{x+c}\cdot1\cdot\frac{\frac{a+c}{2}}{\frac{a-c}{2}} = 1$ $\frac{x}{x+c}\cdot\frac{a+c}{a-c} = 1$ $\frac{x+c}{x}=\frac{a+c}{a-c}$ $\frac{c}{x}=\frac{2c}{a-c}$ $BE=x=\frac{a-c}{2}=BG$ Similarly, $CF=CH$ .

Therefore, $\angle BGE = \angle E$ and $\angle CHF = \angle F$ . Because the splitting lines of $\triangle ABC$ through $M$ and $N$ intersect at $30^\circ$ , $\angle NOF$ = $30^\circ$ . $\angle BGE+\angle CHF=\angle BGE+\angle CHF=\angle NOF=30^\circ$ .

We conclude that $\angle A=360^\circ-\angle E-\angle F-\angle EOF(reflex)=360^\circ-30^\circ-210^\circ=120^\circ$

Apply the Law of Cosines on $\triangle ABC$

$c^2+a^2-2ac\cos 120^\circ=219^2$

$a^2+c^2+ac=219^2=47961$

To find the final answer, you would only need to solve this equation, which steps could be found in previous solutions.

~cassphe

Video Solution

https://youtu.be/T6zq1e1RZdg

~MathProblemSolvingSkills.com

Video Solution

https://www.youtube.com/watch?v=kkous52vPps&t=3023s

~Steven Chen (wwww.professorchenedu.com)

Animated Video Solution

https://youtu.be/o-aDdxdnTWY

~Star League (https://starleague.us)

@@ Line 300: / Line 300: @@
 '''vladimir.shelomovskii@gmail.com, vvsss'''
-==Solution (Geometry Part)==
+==Solution (The Geometry Part Using Menelaus)==
 [[File:2022AIME1.png|500px]]
@@ Line 341: / Line 341: @@
 To find the final answer, you would only need to solve this equation, which steps could be found in previous solutions.
-~cassphe_
+~cassphe
 ==Video Solution==

2022 AIME I (Problems • Answer Key • Resources)
Preceded by Problem 13	Followed by Problem 15
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

Page

Toolbox

Search

Difference between revisions of "2022 AIME I Problems/Problem 14"

Latest revision as of 04:07, 4 May 2025

Contents

Problem

The Geometry Part - Solution 1

The Geometry Part - Solution 2

The NT Part

Solution (Geometry + Number Theory)

Solution (Number Theory Part)

Solution(Visual geometry)

Solution (The Geometry Part Using Menelaus)

Video Solution

Video Solution

Animated Video Solution

See Also