Difference between revisions of "2023 AIME I Problems/Problem 15"

Revision as of 10:22, 2 June 2025

Problem

Find the largest prime number $p<1000$ for which there exists a complex number $z$ satisfying

the real and imaginary part of $z$ are both integers;
$|z|=\sqrt{p},$ and
there exists a triangle whose three side lengths are $p,$ the real part of $z^{3},$ and the imaginary part of $z^{3}.$

Solution

Assume that $z=a+bi$ . Then, $z^3=(a^3-3ab^2)+(3a^2b-b^3)i$ Note that by the Triangle Inequality, $|(a^3-3ab^2)-(3a^2b-b^3)|<p\implies |a^3+b^3-3ab^2-3a^2b|<a^2+b^2$ Thus, we know $|a+b||a^2+b^2-4ab|<a^2+b^2$ Without loss of generality, assume $a>b$ (as otherwise, consider $i^3\overline z=b+ai$ ). If $|a/b|\geq 4$ , then $17b^2\geq a^2+b^2>|a+b||a^2+b^2-4ab|\geq |b-4b||16b^2-16b^2+b^2|=3b^3$ `Thus, this means $b\leq\frac{17}3$ or $b\leq 5$ . Also note that the roots of $x^2-4x+1$ are $2\pm\sqrt 3$ , so thus if $b\geq 6$ , $2\sqrt 3b=(2(2-\sqrt 3)-4)b<a<4b$ Note that $1000>p=a^2+b^2\geq 12b^2+b^2=13b^2$ so $b^2<81$ , and $b<9$ . If $b=8$ , then $16\sqrt 3\leq a\leq 32$ . Note that $\gcd(a,b)=1$ , and $a\not\equiv b\pmod 2$ , so $a=29$ or $31$ . However, then $5\mid a^2+b^2$ , absurd.

If $b=7$ , by similar logic, we have that $14\sqrt 3 <a< 28$ , so $a=26$ . However, once again, $5\mid a^2+b^2$ . If $b=6$ , by the same logic, $12\sqrt3<a<24$ , so $a=23$ , where we run into the same problem. Thus $b\leq 5$ indeed.

If $b=5$ , note that $(a+5)(a^2+25-20a)<a^2+25\implies a<20$ We note that $p=5^2+18^2=349$ works. Thus, we just need to make sure that if $b\leq 4$ , $a\leq 18$ . But this is easy, as $p>(a+b)(a^2+b^2-4ab)\geq (4+18)(4^2+18^2-4\cdot 4\cdot 18)>1000$ absurd. Thus, the answer is $\boxed{349}$ .

Solution 2

Denote $z = a + i b$ . Thus, $a^2 + b^2 = p$ .

Thus, $z^3 = a \left( a^2 - 3 b^2 \right) + i b \left( - b^2 + 3 a^2 \right) .$

Because $p$ , ${\rm Re} \left( z^3 \right)$ , ${\rm Im} \left( z^3 \right)$ are three sides of a triangle, we have ${\rm Re} \left( z^3 \right) > 0$ and ${\rm Im} \left( z^3 \right) > 0$ . Thus, $\begin{align*} a \left( a^2 - 3 b^2 \right) & > 0 , \hspace{1cm} (1) \\ b \left( - b^2 + 3 a^2 \right) & > 0. \hspace{1cm} (2) \end{align*}$

Because $p$ , ${\rm Re} \left( z^3 \right)$ , ${\rm Im} \left( z^3 \right)$ are three sides of a triangle, we have the following triangle inequalities: $\begin{align*} {\rm Re} \left( z^3 \right) + {\rm Im} \left( z^3 \right) & > p \hspace{1cm} (3) \\ p + {\rm Re} \left( z^3 \right) & > {\rm Im} \left( z^3 \right) \hspace{1cm} (4) \\ p + {\rm Im} \left( z^3 \right) & > {\rm Re} \left( z^3 \right) \hspace{1cm} (5) \end{align*}$

We notice that $| z^3 | = p^{3/2}$ , and ${\rm Re} \left( z^3 \right)$ , ${\rm Im} \left( z^3 \right)$ , and $| z^3 |$ form a right triangle. Thus, ${\rm Re} \left( z^3 \right) + {\rm Im} \left( z^3 \right) > p^{3/2}$ . Because $p > 1$ , $p^{3/2} > p$ . Therefore, (3) holds.

Conditions (4) and (5) can be written in the joint form as $\left| {\rm Re} \left( z^3 \right) - {\rm Im} \left( z^3 \right) \right| < p . \hspace{1cm} (4)$

We have $\begin{align*} {\rm Re} \left( z^3 \right) - {\rm Im} \left( z^3 \right) & = \left( a^3 - 3 a b^2 \right) - \left( - b^3 + 3 a^2 b \right) \\ & = \left( a + b \right) \left( a^2 - 4 ab + b^2 \right) \end{align*}$ and $p = a^2 + b^2$ .

Thus, (5) can be written as $\left| \left( a + b \right) \left( a^2 - 4 ab + b^2 \right) \right| < a^2 + b^2 . \hspace{1cm} (6)$

Therefore, we need to jointly solve (1), (2), (6). From (1) and (2), we have either $a, b >0$ , or $a, b < 0$ . In (6), by symmetry, without loss of generality, we assume $a, b > 0$ .

Thus, (1) and (2) are reduced to $a > \sqrt{3} b . \hspace{1cm} (7)$

Let $a = \lambda b$ . Plugging this into (6), we get $\begin{align*} \left| \left( \left( \lambda - 2 \right)^2 - 3 \right) \right| < \frac{1}{b} \frac{\lambda^2 + 1}{\lambda + 1} . \hspace{1cm} (8) \end{align*}$

Because $p= a^2 + b^2$ is a prime, $a$ and $b$ are relatively prime.

Therefore, we can use (7), (8), $a^2 + b^2 <1000$ , and $a$ and $b$ are relatively prime to solve the problem.

To facilitate efficient search, we apply the following criteria:

To satisfy (7) and $a^2 + b^2 < 1000$ , we have $1 \leq b \leq 15$ . In the outer layer, we search for $b$ in a decreasing order. In the inner layer, for each given $b$ , we search for $a$ . Given $b$ , we search for $a$ in the range $\sqrt{3} b < a < \sqrt{1000 - b^2}$ . We can prove that for $b \geq 9$ , there is no feasible $a$ . The proof is as follows.

For $b \geq 9$ , to satisfy $a^2 + b^2 < 1000$ , we have $a \leq 30$ . Thus, $\sqrt{3} < \lambda \leq \frac{30}{9}$ . Thus, the R.H.S. of (8) has the following upper bound $\begin{align*} \frac{1}{b} \frac{\lambda^2 + 1}{\lambda + 1} & < \frac{1}{b} \frac{\lambda^2 + \lambda}{\lambda + 1} \\ & = \frac{\lambda}{b} \\ & \leq \frac{\frac{30}{9}}{9} \\ & < \frac{10}{27} . \end{align*}$

Hence, to satisfy (8), a necessary condition is $\begin{align*} \left| \left( \left( \lambda - 2 \right)^2 - 3 \right) \right| < \frac{10}{27} . \end{align*}$

However, this cannot be satisfied for $\sqrt{3} < \lambda \leq \frac{30}{9}$ . Therefore, there is no feasible solution for $b \geq 9$ . Therefore, we only need to consider $b \leq 8$ .

We eliminate $a$ that is not relatively prime to $b$ .

We use the following criteria to quickly eliminate $a$ that make $a^2 + b^2$ a composite number.

For $b \equiv 1 \pmod{2}$ , we eliminate $a$ satisfying $a \equiv 1 \pmod{2}$ .

For $b \equiv \pm 1 \pmod{5}$ (resp. $b \equiv \pm 2 \pmod{5}$ ), we eliminate $a$ satisfying $a \equiv \pm 2 \pmod{5}$ (resp. $a \equiv \pm 1 \pmod{5}$ ).

\item For the remaining $\left( b, a \right)$ , check whether (8) and the condition that $a^2 + b^2$ is prime are both satisfied.

The first feasible solution is $b = 5$ and $a = 18$ . Thus, $a^2 + b^2 = 349$ .

\item For the remaining search, given $b$ , we only search for $a \geq \sqrt{349 - b^2}$ .

Following the above search criteria, we find the final answer as $b = 5$ and $a = 18$ . Thus, the largest prime $p$ is $p = a^2 + b^2 = \boxed{\textbf{(349) }}$ .

~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)

Solution 3

Let $z = a + b i (a,b\in I)$ . $a^2 + b^2 = prime < 1000$ , $(a,b) = 1$ .

According to the question, ${\rm Re} \left( z^3 \right)$ , ${\rm Im} \left( z^3 \right)$ , and $|z^3|$ construct the side-lengths of a non-degenerate triangle.

$z^3 = (a+bi)^3 = a^3+3a^2bi-3ab^2-b^3i = (a^3 - 3ab^2) + (3a^2b-b^3)i$

${\rm Re} \left( z^3 \right) = a^3 - 3ab^2 > 0 => a(a^2 - 3b^2) > 0$

${\rm Im} \left( z^3 \right) = a^3 - 3ab^2 > 0 => a(a^2 - 3b^2) > 0$

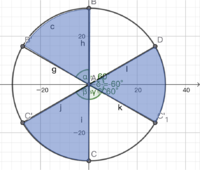
This means that the values of $a$ and $b$ should be limited in the colored areas.

Also

${\rm Re} \left( z^3 \right) + {\rm Im} \left( z^3 \right) > |z^3| > |z||z^2|>|z^2|$

$|{\rm Re} \left( z^3 \right) - {\rm Im} \left( z^3 \right)| < |z|^2$

$|a^3-3ab^2-(3a^2b-b^3)| < a^2+b^2$

$=|a^3-3ab^2+b^3-3a^2b|$

$=|a^3+b^3-3ab(a+b)|$

$=|a+b||a^2-4ab+b^2|<a^2+b^2 (*)$

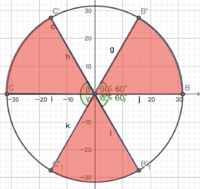
If $a<0,b>0$ , $|a^2-4ab+b^2|>|a^2+b^2|$ , making statement $(*)$ false. Combining with the former graph depicting possible ranges of $a,b$ , by loss of generality, we assume $a,b$ both $>0$ and exists in the first $30^{\circ}$ of the circle.

Let $\frac{a}{b} = \lambda > \sqrt{3}$ .

$(*) |b^3(1+\lambda)\cdot({\lambda}^{2}-4\lambda+1)| < b^2(1+{\lambda}^{2})$

$b<|\frac{1+{\lambda}^2}{1+\lambda}|\cdot|\frac{1}{{\lambda}^{2}-4\lambda+1}|$

After graphing out $|\frac{1+{\lambda}^2}{1+\lambda}|$ and $|{\lambda}^{2}-4\lambda+1|$ , we find out that when $\lambda$ is around $2+\sqrt{3}$ , b reaches its maximum upper bound.

$b^2(1+{\lambda}^{2}) < 1000$

$b^2<66$

$b\le 8$

Testing values of $b$ in decreasing order, starting from 8, we test out each corresponding value of $a$ ( $b\cdot\lambda$ )by trying the two whole numbers closest to the real value of $a$ .

We finally get that $b=5, a=18$ and $p = 5^2+18^2 = \boxed{349}$

~cassphe

Video Solution

https://youtu.be/V0KFMIXmp08

~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)

Video Solution

https://youtu.be/tELK8fy36bs

~MathProblemSolvingSkills.com

Animated Video Solution

https://youtu.be/1Y8ql7eHt34

~Star League (https://starleague.us)

@@ Line 182: / Line 182: @@
 Combining with the former graph depicting possible ranges of <math>a,b</math>, by loss of generality, we assume <math>a,b</math> both <math>>0</math> and exists in the first <math>30^{\circ}</math> of the circle.
-Let <math>\frac{a}{b} = \lambda < \sqrt{3}</math>.
+Let <math>\frac{a}{b} = \lambda > \sqrt{3}</math>.
 <math>(*) |b^3(1+\lambda)\cdot({\lambda}^{2}-4\lambda+1)| < b^2(1+{\lambda}^{2})</math>
-<math>b<|\frac{1+x^2}{1+\lambda}|\cdot|\frac{1}{{\lambda}^{2}-4\lambda+1}|</math>
+<math>b<|\frac{1+{\lambda}^2}{1+\lambda}|\cdot|\frac{1}{{\lambda}^{2}-4\lambda+1}|</math>
-After graphing out <math>|\frac{1+x^2}{1+\lambda}|</math> and <math>{\lambda}^{2}-4\lambda+1</math>, we find out that when <math>\lambda</math> is around <math>2+\sqrt{3}</math>, b reaches its maximum upper bound.
+After graphing out <math>|\frac{1+{\lambda}^2}{1+\lambda}|</math> and <math>|{\lambda}^{2}-4\lambda+1|</math>, we find out that when <math>\lambda</math> is around <math>2+\sqrt{3}</math>, b reaches its maximum upper bound.
 <math>b^2(1+{\lambda}^{2}) < 1000</math>

2023 AIME I (Problems • Answer Key • Resources)
Preceded by Problem 14	Followed by Last Problem
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

Page

Toolbox

Search

Difference between revisions of "2023 AIME I Problems/Problem 15"

Revision as of 10:22, 2 June 2025

Contents

Problem

Solution

Solution 2

Solution 3

Video Solution

Video Solution

Animated Video Solution

See also