Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2005 AMC 12A Problems/Problem 16"

(Undo revision 225329 by Natboy12 (talk))
(Tag: Undo)
m (Removed unnecessary links in problem statement)
Line 1: Line 1:
 
== Problem ==
 
== Problem ==
−
Three [[circle]]s of [[radius]] <math>s</math> are drawn in the first [[quadrant]] of the <math>xy</math>-[[plane]]. The first circle is tangent to both axes, the second is [[tangent (geometry)|tangent]] to the first circle and the <math>x</math>-axis, and the third is tangent to the first circle and the <math>y</math>-axis. A circle of radius <math>r > s</math> is tangent to both axes and to the second and third circles. What is <math>r/s</math>?
+
Three circles of radius <math>s</math> are drawn in the first quadrant of the <math>xy</math>-plane. The first circle is tangent to both axes, the second is tangent to the first circle and the <math>x</math>-axis, and the third is tangent to the first circle and the <math>y</math>-axis. A circle of radius <math>r > s</math> is tangent to both axes and to the second and third circles. What is <math>r/s</math>?
  
 
<asy>
 
<asy>

Revision as of 14:56, 1 July 2025

Problem

Three circles of radius $s$ are drawn in the first quadrant of the $xy$-plane. The first circle is tangent to both axes, the second is tangent to the first circle and the $x$-axis, and the third is tangent to the first circle and the $y$-axis. A circle of radius $r > s$ is tangent to both axes and to the second and third circles. What is $r/s$?

[asy] unitsize(3mm); defaultpen(linewidth(.8pt)+fontsize(10pt)); dotfactor=3; pair O0=(9,9), O1=(1,1), O2=(3,1), O3=(1,3); pair P0=O0+9*dir(-45), P3=O3+dir(70); pair[] ps={O0,O1,O2,O3}; dot(ps); draw(Circle(O0,9)); draw(Circle(O1,1)); draw(Circle(O2,1)); draw(Circle(O3,1)); draw(O0--P0,linetype("3 3")); draw(O3--P3,linetype("2 2")); draw((0,0)--(18,0)); draw((0,0)--(0,18)); label("$r$",midpoint(O0--P0),NE); label("$s$",(-1.5,4)); draw((-1,4)--midpoint(O3--P3));[/asy]

$(\mathrm {A}) \ 5 \qquad (\mathrm {B}) \ 6 \qquad (\mathrm {C})\ 8 \qquad (\mathrm {D}) \ 9 \qquad (\mathrm {E})\ 10$

Solution

Solution 1

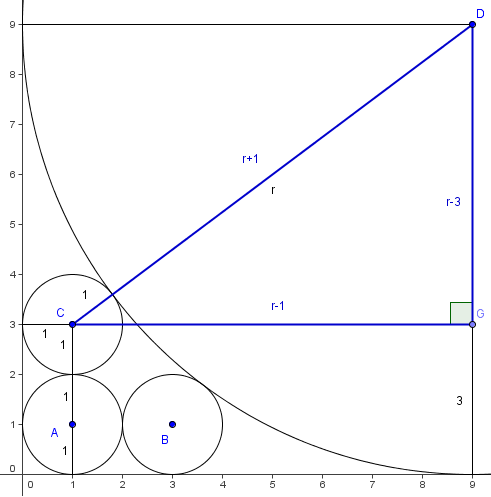
2005 12A AMC-16b.png

Set $s =1$ so that we only have to find $r$. Draw the segment between the center of the third circle and the large circle; this has length $r+1$. We then draw the radius of the large circle that is perpendicular to the x-axis, and draw the perpendicular from this radius to the center of the third circle. This gives us a right triangle with legs $r-3,r-1$ and hypotenuse $r+1$. The Pythagorean Theorem yields:

$(r-3)^2 + (r-1)^2 = (r+1)^2$
$r^2 - 10r + 9 = 0$
$r = 1, 9$

Quite obviously $r > 1$, so $r = 9$.

See also

2005 AMC 12A (Problems • Answer Key • Resources)
Preceded by
Problem 15 		Followed by
Problem 17
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. AMC Logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2005_AMC_12A_Problems/Problem_16&oldid=253027"