Difference between revisions of "2018 AIME I Problems/Problem 1"

Latest revision as of 12:02, 1 August 2025

1 Problem 1
2 Solution 1
3 Solution 2
4 Solution 3 (less complicated)
5 Solution 4
- 5.1 Ending 1
- 5.2 Ending 2
6 Solution 5
7 Solution 6(simple)
8 Solution 7 (less room for error)
9 Solution 8 (Sticks and stones)
10 Solution 9 (Official MAA)
11 Solution 10 (Extra solution that is very very similar to the other solutions)
12 Video Solution
13 See Also

Problem 1

Let $S$ be the number of ordered pairs of integers $(a,b)$ with $1 \leq a \leq 100$ and $b \geq 0$ such that the polynomial $x^2+ax+b$ can be factored into the product of two (not necessarily distinct) linear factors with integer coefficients. Find the remainder when $S$ is divided by $1000$ .

Solution 1

Let the linear factors be $(x+c)(x+d)$ .

Then, $a=c+d$ and $b=cd$ .

We know that $1\le a\le 100$ and $b\ge 0$ , so $c$ and $d$ both have to be non-negative

However, $a$ cannot be $0$ , so at least one of $c$ and $d$ must be greater than $0$ , ie positive.

Also, $a$ cannot be greater than $100$ , so $c+d$ must be less than or equal to $100$ .

Essentially, if we plot the solutions, we get a triangle on the coordinate plane with vertices $(0,0), (0, 100),$ and $(100,0)$ . Remember that $(0,0)$ does not work, so there is a square with the top right corner $(1,1)$ .

Note that $c$ and $d$ are interchangeable since they end up as $a$ and $b$ in the end anyways. Thus, we simply draw a line from $(1,1)$ to $(50,50)$ , designating one of the halves as our solution (since the other side is simply the coordinates flipped).

We note that the pattern from $(1,1)$ to $(50,50)$ is $2+3+4+\dots+51$ solutions and from $(51, 49)$ to $(100,0)$ is $50+49+48+\dots+1$ solutions, since we can decrease the $y$ -value by $1$ until $0$ for each coordinate.

Adding up gives $\dfrac{2+51}{2}\cdot 50+\dfrac{50+1}{2}\cdot 50.$ This gives us $2600$ , and $2600\equiv 600 \bmod{1000}.$

Thus, the answer is: $\boxed{600}.$

~Minor edit by Yiyj1

Solution 2

Similar to the previous solution, we plot the triangle and cut it in half. Then, we find the number of boundary points, which is $101+51+51-3$ , or just $200$ . Using Pick's theorem, we know that the area of the half-triangle, which is $2500$ , is just $I+100-1$ . That means that there are $2401$ interior points, plus $200$ boundary points, which is $2601$ . However, $(0,0)$ does not work, so the answer is $\boxed{600}.$

Solution 3 (less complicated)

Notice that for $x^2+ax+b$ to be true, for every $a$ , $b$ will always be the product of the possibilities of how to add two integers to $a$ . For example, if $a=3$ , $b$ will be the product of $(3,0)$ and $(2,1)$ , as those two sets are the only possibilities of adding two integers to $a$ . Note that order does not matter. If we just do some simple casework, we find out that:

if $a$ is odd, there will always be $\left\lceil\frac{a}{2}\right\rceil$ $\left(\text{which is also }\frac{a+1}{2}\right)$ possibilities of adding two integers to $a$ .

if $a$ is even, there will always be $\frac{a}{2}+1$ possibilities of adding two integers to $a$ .

Using the casework, we have $1+2+2+3+3+...50+50+51$ possibilities. This will mean that the answer is $\frac{(1+51)\cdot100}{2}\Rightarrow52\cdot50=2600$ possibilities.

Thus, our solution is $2600\bmod {1000}\equiv\boxed{600}$ .

Solution by IronicNinja~

Solution 4

Let's write the linear factors as $(x+n)(x+m)$ .

Then we can write them as: $a=n+m, b=nm$ .

$n$ or $m$ has to be a positive integer as a cannot be 0.

$n+m$ has to be between $1$ and $100$ , as a cannot be over $100$ .

Excluding $a=1$ , we can see there is always a pair of $2$ a-values for a certain amount of b-values.

For instance, $a=2$ and $a=3$ both have $2$ b-values. $a=4$ and $a=5$ both have $3$ b-values.

We notice the pattern of the number of b-values in relation to the a-values: $1, 2, 2, 3, 3, 4, 4…$

Ending 1

We see the pattern $1, 2; 2, 3; 3, 4; ...$ . There are 50 pairs of $i, i+1$ in this pattern, and each pair sums to $2i+1$ . So the pattern condenses to $3, 5, 7, ...$ for 50 terms. This is just $1+3+5+...$ for 51 terms, minus $1$ , or $51^2-1=2601-1=2600\implies\boxed{600}$ .

~ Firebolt360

Ending 2

The following link is the URL to the graph I drew showing the relationship between a-values and b-values http://artofproblemsolving.com/wiki/index.php?title=File:Screen_Shot_2018-04-30_at_8.15.00_PM.png#file

The pattern continues until $a=100$ , and in total, there are $49$ pairs of a-value with the same amount of b-values. The two lone a-values without a pair are, the ( $a=1$ , amount of b-values=1) in the beginning, and ( $a=100$ , amount of b-values=51) in the end.

Then, we add numbers from the opposite ends of the spectrum, and quickly notice that there are $50$ pairs each with a sum of $52$ . $52\cdot50$ gives $2600$ ordered pairs:

$1+51, 2+50, 2+50, 3+49, 3+49, 4+48, 4+48…$

When divided by $1000$ , it gives the remainder $\boxed{600}$ , the answer.

Solution provided by- Yonglao Slightly modified by Afly

Remark : This solution works because no distinct $(a,b), (c,d)$ exist such that $a+b=c+d,ab=cd$ unless $a = d$ and $b = c$

Solution 5

Let's say that the quadratic $x^2 + ax + b$ can be factored into $(x+c)(x+d)$ where $c$ and $d$ are non-negative numbers. We can't have both of them zero because $a$ would not be within bounds. Also, $c+d \leq 100$ . Assume that $c < d$ . $d$ can be written as $c + x$ where $x \geq 0$ . Therefore, $c + d = 2c + x \leq 100$ . To find the amount of ordered pairs, we must consider how many values of $x$ are possible for each value of $c$ . The amount of possible values of $x$ is given by $100 - 2c + 1$ . The $+1$ is the case where $c = d$ . We don't include the case where $c = d = 0$ , so we must subtract a case from our total. The amount of ordered pairs of $(a,b)$ is: $\left(\sum_{c=0}^{50} (100 - 2c + 1)\right) - 1$ This is an arithmetic progression. $\frac{(101 + 1)(51)}{2} - 1 = 2601 - 1 = 2600$ When divided by $1000$ , it gives the remainder $\boxed{600}$

~Zeric Hang

Solution 6(simple)

By Vietas, the sum of the roots is $-a$ and the product is $b$ . Therefore, both roots are nonpositive. For each value of $a$ from $1$ to $100$ , the number of $b$ values is the number of ways to sum two numbers between $0$ and $a-1$ inclusive to $a$ . This is just $1 + 2 + 2 + 3 + 3 +... 50 + 50 + 51 = 2600$ . Thus, the answer is $\boxed{600}$

-bron jiang

Solution 7 (less room for error)

Similar to solution 1 we plot the triangle and half it. From dividing the triangle in half we are removing the other half of answers that are just flipped coordinates. We notice that we can measure the length of the longest side of the half triangle which is just from $0$ to $100$ , so the number of points on that line is is $101$ . The next row has length $99$ , the one after that has length $97$ , and so on. We simply add this arithmetic series of odd integers $101+99+97+...+1$ . This is $\frac{(101+1)(51)}{2} = 2601$ Or you can notice that this is the sum of the first $51$ odd terms, which is just $51^2 = 2601$ . However, $(0,0)$ is the singular coordinate that does not work, so the answer is $(2601-1)\bmod {1000}\equiv\boxed{600}$

Solution by Damian Kim~

Solution 8 (Sticks and stones)

Letting $-r$ and $-q$ be the roots, we must find the number of unordered pairs $(r,q)$ such that $1 \le r+q \le 100.$ To do this we define three boxes: $r, q,$ and $t$ for "trash." For example, if we had $t=77,$ we would have any arrangement of $r$ and $q$ summing to $23.$ Note that we cannot have $t=100,$ subtracting one from our total. By stars and bars, we have that the number of ordered pairs $(r,q)$ is ${102 \choose 2} - 1 = 5150.$ However, we are not done: we have double-counted cases such as $(1,2)$ and $(2,1)$ but not cases such as $(4,4).$ Thus our answer will be $\frac{5150 - 50}{2} + 50 \pmod {100} = \boxed{600}.$ ~ab2024

Solution 9 (Official MAA)

The factoring condition is equivalent to the discriminant $a^2-4b$ being equal to $c^2$ for some integer $c.$ Because $b\ge 0,$ the equation $4b=(a-c)(a+c)$ shows that the existence of such a $b$ is equivalent to $a\equiv c\pmod 2$ with $0\le c\le a.$ Thus the number of ordered pairs is $S=\sum_{a=1}^{100}\left\lceil\frac{a+1}{2}\right\rceil=2600.$ The requested remainder is $600.$

Solution 10 (Extra solution that is very very similar to the other solutions)

First I thought the special case of the problem is when the factors are repeated, which looks like this:

There are 50 ways for this to happen because r can be from $1$ to $50$ ( $(x+50)^2 = x^2+100x+50^2$ and $a\leq 50$ ).

Now I thought how can you make the other cases? It looks like $(x-r)(x-s)$ so by Vieta's $r+s=a$ . This looks like Stars and Bars

because $a=1+1+1+1+...$ and you're giving the indistinguishable ones to $r$ and $s$ . For $a=1$ , there are $\binom{1+2-1}{2-1} = 2$

ways. For $a=2$ , there are $\binom{2+2-1}{2-1} = 3$ ways. Now you see the pattern which is $2+3+...+100+101$ for $a=1, 2, ...100$ .

This equals $103\cdot50$ ways in total. However, now you realize that $r$ and $s$ can be flipped and it gives the same. So,

subtract the cases when $r = s$ which we found to be $50$ . Now from the remaining double-counted $102\cdot50$ divide by two to

eliminate the double-counting. We have $51\cdot50$ , but remember to add back in the $50$ ways that weren't double-counted to begin

with. That gives us $52\cdot50 = 2600$ ways and the requested remainder is $600.$

-unhappyfarmer

Video Solution

https://www.youtube.com/watch?v=WVtbD8x9fCM ~Shreyas S

@@ Line 2: / Line 2: @@
 Let <math>S</math> be the number of ordered pairs of integers <math>(a,b)</math> with <math>1 \leq a \leq 100</math> and <math>b \geq 0</math> such that the polynomial <math>x^2+ax+b</math> can be factored into the product of two (not necessarily distinct) linear factors with integer coefficients. Find the remainder when <math>S</math> is divided by <math>1000</math>.
-==Solution==
+==Solution 1==
-You let the linear factors be as <math>(x+c)(x+d)</math>.
+Let the linear factors be <math>(x+c)(x+d)</math>.
-Then, obviously <math>a=c+d</math> and <math>b=cd</math>.
+Then, <math>a=c+d</math> and <math>b=cd</math>.
 We know that <math>1\le a\le 100</math> and <math>b\ge 0</math>, so <math>c</math> and <math>d</math> both have to be non-negative
@@ Line 14: / Line 14: @@
 Also, <math>a</math> cannot be greater than <math>100</math>, so <math>c+d</math> must be less than or equal to <math>100</math>.
-Essentially, if we plot the solutions, we get a triangle on the coordinate plane with vertices <math>(0,0), (0, 100),</math> and <math>(100,0)</math>. Remember that <math>(0,0)</math> does not work, so there is a square with top right corner <math>(1,1)</math>.
+Essentially, if we plot the solutions, we get a triangle on the coordinate plane with vertices <math>(0,0), (0, 100),</math> and <math>(100,0)</math>. Remember that <math>(0,0)</math> does not work, so there is a square with the top right corner <math>(1,1)</math>.
-Note that <math>c</math> and <math>d</math> are interchangeable, since they end up as <math>a</math> and <math>b</math> in the end anyways. Thus, we simply draw a line from <math>(1,1)</math> to <math>(50,50)</math>, designating one of the halves as our solution (since the other side is simply the coordinates flipped).
+Note that <math>c</math> and <math>d</math> are interchangeable since they end up as <math>a</math> and <math>b</math> in the end anyways. Thus, we simply draw a line from <math>(1,1)</math> to <math>(50,50)</math>, designating one of the halves as our solution (since the other side is simply the coordinates flipped).
 We note that the pattern from <math>(1,1)</math> to <math>(50,50)</math> is <math>2+3+4+\dots+51</math> solutions and from <math>(51, 49)</math> to <math>(100,0)</math> is <math>50+49+48+\dots+1</math> solutions, since we can decrease the <math>y</math>-value by <math>1</math> until <math>0</math> for each coordinate.
@@ Line 24: / Line 24: @@
 Thus, the answer is: <cmath>\boxed{600}.</cmath>
+~Minor edit by Yiyj1
 ==Solution 2==
-Similar to the previous problem, we plot the triangle and cut it in half. Then, we find the number of boundary points, which is <math>101+51+51-3</math>, or just <math>200</math>. Using Pick's theorem, we know that the area of the half-triangle, which is <math>2500</math>, is just <math>I+100-1</math>. That means that there are <math>2401</math> interior points, plus <math>200</math> boundary points, which is <math>2601</math>. However, <math>(0,0)</math> does not work, so the answer is <cmath>\boxed{600}.</cmath>
+Similar to the previous solution, we plot the triangle and cut it in half. Then, we find the number of boundary points, which is <math>101+51+51-3</math>, or just <math>200</math>. Using Pick's theorem, we know that the area of the half-triangle, which is <math>2500</math>, is just <math>I+100-1</math>. That means that there are <math>2401</math> interior points, plus <math>200</math> boundary points, which is <math>2601</math>. However, <math>(0,0)</math> does not work, so the answer is <cmath>\boxed{600}.</cmath>
 ==Solution 3 (less complicated)==
@@ Line 59: / Line 61: @@
 <math>1, 2, 2, 3, 3, 4, 4…</math>
+=== Ending 1 ===
+We see the pattern <math>1, 2; 2, 3; 3, 4; ...</math>. There are 50 pairs of <math>i, i+1</math> in this pattern, and each pair sums to <math>2i+1</math>. So the pattern condenses to <math>3, 5, 7, ...</math> for 50 terms. This is just <math>1+3+5+...</math> for 51 terms, minus <math>1</math>, or <math>51^2-1=2601-1=2600\implies\boxed{600}</math>.
+~ Firebolt360
+=== Ending 2 ===
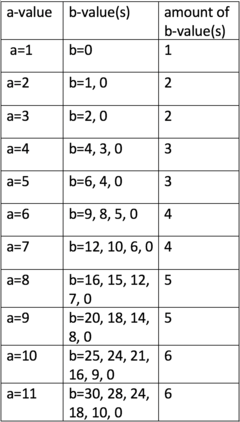
 The following link is the URL to the graph I drew showing the relationship between a-values and b-values
 http://artofproblemsolving.com/wiki/index.php?title=File:Screen_Shot_2018-04-30_at_8.15.00_PM.png#file
+[[File:Screen Shot 2018-04-30 at 8.15.00 PM.png|thumb|240px]]
 The pattern continues until <math>a=100</math>, and in total, there are <math>49</math> pairs of a-value with the same amount of b-values. The two lone a-values without a pair are, the (<math>a=1</math>, amount of b-values=1) in the beginning, and (<math>a=100</math>, amount of b-values=51) in the end.
@@ Line 71: / Line 80: @@
 Solution provided by- Yonglao
+Slightly modified by Afly
+Remark : This solution works because
+no distinct <math>(a,b), (c,d)</math> exist such that <math>a+b=c+d,ab=cd</math> unless <math>a = d</math> and <math>b = c</math>
 ==Solution 5==
@@ Line 93: / Line 107: @@
 Solution by Damian Kim~
+==Solution 8 (Sticks and stones)==
+Letting <math>-r</math> and <math>-q</math> be the roots, we must find the number of unordered pairs <math>(r,q)</math> such that <math>1 \le r+q \le 100.</math> To do this we define three boxes: <math>r, q,</math> and <math>t</math> for "trash." For example, if we had <math>t=77,</math> we would have any arrangement of <math>r</math> and <math>q</math> summing to <math>23.</math> Note that we cannot have <math>t=100,</math> subtracting one from our total. By stars and bars, we have that the number of ordered pairs <math>(r,q)</math> is <math>{102 \choose 2} - 1 = 5150.</math> However, we are not done: we have double-counted cases such as <math>(1,2)</math> and <math>(2,1)</math> but not cases such as <math>(4,4).</math> Thus our answer will be <math>\frac{5150 - 50}{2} + 50 \pmod {100} = \boxed{600}.</math>
+~ab2024
+==Solution 9 (Official MAA)==
+The factoring condition is equivalent to the discriminant <math>a^2-4b</math> being equal to <math>c^2</math> for some integer <math>c.</math> Because <math>b\ge 0,</math> the equation <math>4b=(a-c)(a+c)</math> shows that the existence of such a <math>b</math> is equivalent to <math>a\equiv c\pmod 2</math> with <math>0\le c\le a.</math> Thus the number of ordered pairs is <cmath>S=\sum_{a=1}^{100}\left\lceil\frac{a+1}{2}\right\rceil=2600.</cmath> The requested remainder is <math>600.</math>
+==Solution 10 (Extra solution that is very very similar to the other solutions)==
+First I thought the special case of the problem is when the factors are repeated, which looks like this:
+  <math>(x+r)^2</math>
+There are 50 ways for this to happen because r can be from <math>1</math> to <math>50</math> (<math>(x+50)^2 = x^2+100x+50^2</math> and <math>a\leq 50</math>).
+Now I thought how can you make the other cases? It looks like <math>(x-r)(x-s)</math> so by Vieta's <math>r+s=a</math>. This looks like Stars and Bars
+because <math>a=1+1+1+1+...</math> and you're giving the indistinguishable ones to <math>r</math> and <math>s</math>. For <math>a=1</math>, there are <math>\binom{1+2-1}{2-1} = 2</math>
+ways. For <math>a=2</math>, there are <math>\binom{2+2-1}{2-1} = 3</math> ways. Now you see the pattern which is <math>2+3+...+100+101</math> for <math>a=1, 2, ...100</math>.
+This equals <math>103\cdot50</math> ways in total. However, now you realize that <math>r</math> and <math>s</math> can be flipped and it gives the same. So,
+subtract the cases when <math>r = s</math> which we found to be <math>50</math>. Now from the remaining double-counted <math>102\cdot50</math> divide by two to
+eliminate the double-counting. We have <math>51\cdot50</math>, but remember to add back in the <math>50</math> ways that weren't double-counted to begin
+with. That gives us <math>52\cdot50 = 2600</math> ways and the requested remainder is <math>600.</math>
+-unhappyfarmer
 ==Video Solution==
-https://www.youtube.com/watch?v=WVtbD8x9fCM https://www.youtube.com/watch?v=WVtbD8x9fCM
+https://www.youtube.com/watch?v=WVtbD8x9fCM
 ~Shreyas S

2018 AIME I (Problems • Answer Key • Resources)
Preceded by First Problem	Followed by Problem 2
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

Page

Toolbox

Search