Difference between revisions of "Isogonal conjugate"

Latest revision as of 13:25, 7 August 2025

Isogonal conjugates are pairs of points in the plane with respect to a certain triangle.

1 The isogonal theorem
- 1.1 Isogonal lines definition
- 1.2 Projective transformation
- 1.3 The isogonal theorem
  - 1.3.1 Proof
- 1.4 The isogonal theorem in the case of parallel lines
  - 1.4.1 Proof
- 1.5 Converse theorem
  - 1.5.1 Proof
2 Parallel segments
3 Perpendicularity
4 Fixed point
5 Bisector
6 Isogonal of the diagonal of a quadrilateral
7 Isogonals in trapezium
8 Isogonals in complete quadrilateral
9 Isogonal of the bisector of the triangle
10 Points on isogonals
11 Trapezoid
12 Definition of isogonal conjugate of a point
13 Three points
14 Second definition
15 Distance to the sides of the triangle
16 Sign of isogonally conjugate points
17 Circumcircle of pedal triangles
18 Common circumcircle of the pedal triangles as the sign of isogonally conjugate points
19 Two pares of isogonally conjugate points
20 Circles
21 Equidistant isogonal conjugate points
22 Simplified distance formula for isogonal points
23 Point on circumcircle
24 Fixed point on circumcircle
25 Distance formula for isogonal points
26 Miquel point for isogonal conjugate points
27 Point on circumcircle
- 27.1 Simplified problem
28 Isogonal of line BC with respect to angle BAC
29 Isogonal bijection lines and points
30 Miquel point for two pare isogonal points
31 Isogonic center’s conjugate point
32 Three pairs isogonal points
33 Ratio for three pairs of isogonal points
34 Problems

The isogonal theorem

Isogonal lines definition

Let a line $\ell$ and a point $O$ lying on $\ell$ be given. A pair of lines symmetric with respect to $\ell$ and containing the point $O$ be called isogonals with respect to the pair $(\ell,O).$

Sometimes it is convenient to take one pair of isogonals as the base one, for example, $OA$ and $OB$ are the base pair. Then we call the remaining pairs as isogonals with respect to the angle $\angle AOB.$

Projective transformation

It is known that the transformation that maps a point with coordinates $(x,y)$ into a point with coordinates $(\frac{1}{x}, \frac {y}{x}),$ is projective.

If the abscissa axis coincides with the line $\ell$ and the origin coincides with the point $O,$ then the isogonals define the equations $y = \pm kx,$ and the lines $(\frac{1}{x}, \pm k)$ symmetrical with respect to the line $\ell$ become their images.

It is clear that, under the converse transformation (also projective), such pairs of lines become isogonals, and the points equidistant from $\ell$ lie on the isogonals.

The isogonal theorem

Let two pairs of isogonals $OX - OX'$ and $OY - OY'$ with respect to the pair $(\ell,O)$ be given. Denote $Z = XY \cap X'Y', Z' = X'Y \cap XY'.$

Prove that $OZ$ and $OZ'$ are the isogonals with respect to the pair $(\ell,O).$

Proof

Let us perform a projective transformation of the plane that maps the point $O$ into a point at infinity and the line $\ell$ maps to itself. In this case, the isogonals turn into a pair of straight lines parallel to $\ell$ and equidistant from $\ell.$

The converse (also projective) transformation maps the points equidistant from $\ell$ onto isogonals. We denote the image and the preimage with the same symbols.

Let the images of isogonals are vertical lines. Let coordinates of images of points be $X(-a, 0), X'(a,u), Y(-b,v), Y'(b,w).$ Equation of a straight line $XY$ is $\frac{x + a}{a - b} = \frac {y}{v}.$

Equation of a straight line $X'Y'$ is $\frac{x - a}{b - a} = \frac {y - u}{w - u}.$

The abscissa $Z_x$ of the point $Z$ is $Z_x = \frac {v a - a w + u b}{u - v - w}.$

Equation of a straight line $XY'$ is $\frac{x + a}{b + a} = \frac {y}{w}.$

Equation of a straight line $X'Y$ is $\frac{x - a}{- b - a} = \frac {y - u}{v - u}.$

The abscissa $Z'_x$ of the point $Z'$ is $Z'_x = \frac {v a - a w + u b}{- u + v + w} = - Z_x \implies$

Preimages of the points $Z$ and $Z'$ lie on the isogonals. $\blacksquare$

The isogonal theorem in the case of parallel lines

Let $OY$ and $OY'$ are isogonals with respect $\angle XOX'.$

Let lines $XY$ and $X'Y'$ intersect at point $Z, X'Y || XY'.$

Prove that $OZ$ and line $l$ through $O$ parallel to $XY'$ are the isogonals with respect $\angle XOX'.$

Proof

The preimage of $Z'$ is located at infinity on the line $l.$

The equality $Z'_x = -Z_x$ implies the equality the slopes modulo of $OZ$ and $l$ to the bisector of $\angle XOX'. \blacksquare$

Converse theorem

Let lines $XY$ and $X'Y'$ intersect at point $Z, X'Y || XY'.$

Let $OZ$ and $l$ be the isogonals with respect $\angle XOX'.$

Prove that $OY$ and $OY'$ are isogonals with respect $\angle XOX' (\angle XOY' = \angle YOX').$

Proof

The preimage of $Z'$ is located at infinity on the line $l,$ so the slope of $OZ$ is known.

Suppose that $y' \in XY', y' \ne Y', \angle y'OX = \angle YOX'.$

The segment $XY$ and the lines $XY', OZ$ are fixed $\implies$

$y'X'$ intersects $XY$ at $z \ne Z,$

but there is the only point where line $OZ$ intersect $XY.$ Сontradiction. $\blacksquare$

vladimir.shelomovskii@gmail.com, vvsss

Parallel segments

Let triangle $ABC$ be given. Let $AD$ and $AE$ be the isogonals with respect $\angle BAC.$ Let $BD ||CE, P = BE \cap CD.$

Prove that $P$ lies on bisector of $\angle BAC$ and $BD||AP.$

Proof

Both assertions follow from The isogonal theorem in the case of parallel lines

vladimir.shelomovskii@gmail.com, vvsss

Perpendicularity

Let triangle $ABC$ be given. Right triangles $ABD$ and $ACE$ with hypotenuses $AD$ and $AE$ are constructed on sides $AB$ and $AC$ to the outer (inner) side of $\triangle ABC.$ Let $\angle BAD = \angle CAE, H = CD \cap BE.$ Prove that $AH \perp BC.$

Proof

Let $\ell$ be the bisector of $\angle BAC, F = BD \cap CE.$

$AB$ and $AC$ are isogonals with respect to the pair $(\ell,A).$

$AD$ and $AE$ are isogonals with respect to the pair $(\ell,A) \implies$

$AH$ and $AF$ are isogonals with respect to the pair $(\ell,A)$ in accordance with The isogonal theorem.

$\angle ABD = \angle ACE = 90^\circ \implies$

$AF$ is the diameter of circumcircle of $\triangle ABC.$

Circumradius and altitude are isogonals with respect bisector and vertex of triangle, so $AH \perp BC.$ $\blacksquare$

Circumradius

vvsss

Fixed point

Let fixed triangle $ABC$ be given. Let points $D$ and $E$ on sidelines $BC$ and $AB,$ respectively be the arbitrary points.

Let $F$ be the point on sideline $AC$ such that $\angle BDE = \angle CDF.$

$G = BF \cap CE.$ Prove that line $DG$ pass through the fixed point.

Proof

We will prove that point $A',$ symmetric $A$ with respect $\ell = BC,$ lies on $DG$ .

$\angle BDE = \angle CDF \implies DE$ and $DF$ are isogonals with respect to $(\ell, D).$

$A = BE \cap CF \implies$ points $A$ and $G$ lie on isogonals with respect to $(\ell, D)$ in accordance with The isogonal theorem.

Point $A'$ symmetric $A$ with respect $\ell$ lies on isogonal $AD$ with respect to $(\ell, D),$ that is $DG.$ $\blacksquare$

vvsss

Bisector

Let a convex quadrilateral $ABCD$ be given. Let $I$ and $J$ be the incenters of triangles $\triangle ABC$ and $\triangle ADC,$ respectively.

Let $I'$ and $J'$ be the A-excenters of triangles $\triangle ABC$ and $\triangle ADC,$ respectively. $E = IJ' \cap I'J.$

Prove that $CE$ is the bisector of $\angle BCD.$

Proof

$\angle ICI' = \angle JCJ' = 90^\circ \implies$

$CI'$ and $CJ'$ are isogonals with respect to the angle $\angle ICJ.$

$A = II' \cap JJ' \implies AC$ and $EC$ are isogonals with respect to the angle $\angle ICJ$ in accordance with The isogonal theorem.

Denote $\angle ACI = \angle BCI = \alpha, \angle ACJ = \angle DCJ = \beta.$

WLOG, $\beta \ge \alpha.$ $\angle ACJ = \angle ACE + \alpha = \beta,$ $\angle BCE = 2 \alpha + \beta - \alpha = \alpha + \beta = \angle DCE. \blacksquare$

vvsss

Isogonal of the diagonal of a quadrilateral

Given a quadrilateral $ABCD$ and a point $P$ on its diagonal such that $\angle APB = \angle APD.$

Let $E = AB \cap CD, F = AD \cap BC.$

Prove that $\angle BPE = \angle DPF.$

Proof

Let us perform a projective transformation of the plane that maps the point $P$ to a point at infinity and the line $\ell = AC$ into itself.

In this case, the images of points $B$ and $D$ are equidistant from the image of $AC \implies$

the point $M$ (midpoint of $BD)$ lies on $\ell \implies$

$AC$ contains the midpoints of $AC$ and $BD \implies$

$\ell$ is the Gauss line of the complete quadrilateral $ABCDEF \implies$ $\ell$ bisects $EF \implies EE_0 = FF_0 \implies$

the preimages of the points $E$ and $F$ lie on the isogonals $PE$ and $PF. \blacksquare$

vvsss

Isogonals in trapezium

Let the trapezoid $AEFC, AC||EF,$ be given. Denote $B = AE \cap CF, D = AF \cap CE.$

The point $M$ on the smaller base $AC$ is such that $EM = MF.$

Prove that $\angle AMB = \angle AMD.$

Proof

$EM = MF \implies$ $\angle AME = \angle MEF = \angle MFE = \angle CMF.$ Therefore $EM$ and $FM$ are isogonals with respect $(AC,M).$

Let us perform a projective transformation of the plane that maps the point $M$ to a point at infinity and the line $\ell = AC$ into itself.

In this case, the images of points $E$ and $F$ are equidistant from the image of $\ell \implies AC$ contains the midpoints of $AC$ and $EF$ , that is, $\ell$ is the Gauss line of the complete quadrilateral $ABCDEF \implies$

$\ell$ bisects $BD \implies BB_0 = DD_0 \implies$

The preimages of the points $B$ and $D$ lie on the isogonals $MB$ and $MD. \blacksquare$

vvsss

Isogonals in complete quadrilateral

Let complete quadrilateral $ABCDEF (E = AB \cap CD, F = AC \cap BD)$ be given. Let $M$ be the Miquel point of $ABCD.$

Prove that $AM$ is isogonal to $DM$ and $EM$ is isogonal to $FM$ with respect $\angle BMC.$

Proof $\angle BME = \angle BDE = \angle CDF = \angle CMF.$ $\angle BMD = \angle BED = \angle AEC = \angle AMC. \blacksquare$

vvsss

Isogonal of the bisector of the triangle

The triangle $ABC$ be given. The point $D$ chosen on the bisector $AA'.$

Denote $B' = BD \cap AC, C' = CD \cap AB,$ $E = BB' \cap A'C', F = CC' \cap A'B'.$ Prove that $\angle BAE = \angle CAF.$

Proof

Let us perform a projective transformation of the plane that maps the point $A$ to a point at infinity and the line $\ell = AA'$ into itself.

In this case, the images of segments $BC'$ and $B'C$ are equidistant from the image of $\ell \implies BC' || B'C || \ell.$

Image of point $D$ is midpoint of image $BB'$ and midpoint image $CC' \implies$

Image $BCB'C'$ is parallelogramm $\implies$

$BC = B'C' \implies \frac {DE}{BD} = \frac {DF}{CD} \implies$ distances from $E$ and $F$ to $\ell$ are equal $\implies$

Preimages $AE$ and $AF$ are isogonals with respect $(\ell,A). \blacksquare$

vladimir.shelomovskii@gmail.com, vvsss

Points on isogonals

The triangle $ABC$ be given. The point $D$ chosen on $BC.$ The point $E$ chosen on $BC$ such that $AD$ and $AE$ are isogonals with respect $\angle BAC.$

Prove that $\frac {AB^2}{BD \cdot BE} = \frac{ AC^2}{CD \cdot CE}.$

Proof

Denote $\angle BAD = \angle CAE = \varphi,$ $\angle B = \beta, \angle C = \gamma \implies$ $\angle ADE = \beta + \varphi, \angle AED = \gamma + \varphi, \angle BAE = \angle CAD = \psi+\varphi.$

We use the Law of Sines and get: $\frac {AB}{BD} = \frac {\sin (\beta + \varphi)}{\sin \varphi}, \frac {AB}{BE} = \frac {\sin (\gamma + \varphi)}{\sin (\psi +\varphi)},$ $\frac {AC}{CE} = \frac {\sin (\gamma + \varphi)}{\sin \varphi}, \frac {AC}{CD} = \frac {\sin (\beta + \varphi)}{\sin (\psi +\varphi)} \implies$ $\frac {AB \cdot AB}{BD \cdot BE} = \frac {AC \cdot AC}{CD \cdot CE} = \frac {\sin (\beta + \varphi) \cdot \sin (\gamma +\varphi)} {\sin \varphi \cdot \sin (\psi +\varphi)}.$

vladimir.shelomovskii@gmail.com, vvsss

Trapezoid

The lateral side $CD$ of the trapezoid $ABCD$ is perpendicular to the bases, point $P$ is the intersection point of the diagonals $ABCD$ .

Point $Q$ is taken on the circumcircle $\omega$ of triangle $PCD$ diametrically opposite to point $P.$

Prove that $\angle BQC = \angle AQD.$

Proof

WLOG, $CD$ is not the diameter of $\omega.$ Let sidelines $AD$ and $BC$ intersect $\omega$ at points $D'$ and $C',$ respectively.

$DD' \perp CD, CC' \perp CD \implies CDD'C'$ is rectangle $\implies$ $CC' = DD' \implies \angle CQC' = \angle DQD'.$

$QE||BC$ is isogonal to $QO$ with respect $\angle CQD \implies$

$QE||BC$ is isogonal to $QP$ with respect $\angle CQD \implies$

In accordance with The isogonal theorem in case parallel lines $\angle DQO = \angle CQE.$

$QE||BC$ is isogonal to $QP$ with respect $\angle CQD, P = AC \cap BD \implies$

$\angle AQD = \angle BQC$ in accordance with Converse theorem for The isogonal theorem in case parallel lines. $\blacksquare$

vladimir.shelomovskii@gmail.com, vvsss

Definition of isogonal conjugate of a point

Let triangle $\triangle ABC$ be given. Let $\omega$ be the circumcircle of $ABC.$ Let point $P$ be in the plane of $\triangle ABC, P \notin AB, P \notin BC, P \notin AC, P \notin \omega.$ Denote by $a,b,c$ the lines $BC, CA, AB,$ respectively. Denote by $p_a, p_b, p_c$ the lines $PA$ , $PB$ , $PC$ , respectively. Denote by $q_a$ , $q_b$ , $q_c$ the reflections of $p_a$ , $p_b$ , $p_c$ over the angle bisectors of angles $A$ , $B$ , $C$ , respectively.

Prove that lines $q_a$ , $q_b$ , $q_c$ concur at a point $Q.$ This point is called the isogonal conjugate of $P$ with respect to triangle $ABC$ .

Proof

By our constructions of the lines $q$ , $\angle p_a b \equiv \angle q_a c$ , and this statement remains true after permuting $a,b,c$ . Therefore by the trigonometric form of Ceva's Theorem $\frac{\sin \angle q_a b}{\sin \angle c q_a} \cdot \frac{\sin \angle q_b c}{\sin \angle a q_b} \cdot \frac{\sin \angle q_c a}{\sin \angle b q_c} = \frac{\sin \angle p_a c}{\sin \angle b p_a} \cdot \frac{\sin \angle p_b a}{\sin \angle c p_b} \cdot \frac{\sin \angle p_c b}{\sin \angle a p_c} = 1,$ so again by the trigonometric form of Ceva, the lines $q_a, q_b, q_c$ concur, as was to be proven. $\blacksquare$

Corollary

Let points P and Q lie on the isogonals with respect angles $\angle B$ and $\angle C$ of triangle $\triangle ABC.$

Then these points lie on isogonals with respect angle $\angle A.$

Corollary 2

Let point $P$ be in the sideline $BC$ of $\triangle ABC, P \ne B, P \ne C.$

Then the isogonal conjugate of a point $P$ is a point $A.$

Points $A,B,$ and $C$ do not have an isogonally conjugate point.

vladimir.shelomovskii@gmail.com, vvsss

Three points

Let fixed triangle $ABC$ be given. Let the arbitrary point $D$ not be on sidelines of $\triangle ABC.$ Let $E$ be the point on isogonal of $CD$ with respect angle $\angle ACB.$ Let $F$ be the crosspoint of isogonal of $BD$ with respect angle $\angle ABC$ and isogonal of $AE$ with respect angle $\angle BAC.$

Prove that lines $AD, BE,$ and $CF$ are concurrent.

Proof

Denote $D' = BF \cap CE, S = CF \cap BE.$

$AE$ and $AF$ are isogonals with respect $\angle BAC \implies$

$D'$ and S lie on isogonals of $\angle BAC.$

$\angle DBC = \angle D'BA, \angle DCB = \angle D'CA \implies$

$D'$ is isogonal conjugated of $D$ with respect $\triangle ABC \implies$

$D'$ and $D$ lie on isogonals of $\angle BAC.$

Therefore points $A, S$ and $D$ lie on the same line which is isogonal to $AD'$ with respect $\angle BAC. \blacksquare$

vladimir.shelomovskii@gmail.com, vvsss

Second definition

Let triangle $\triangle ABC$ be given. Let point $P$ lies in the plane of $\triangle ABC,$ $P \notin AB, P \notin BC, P \notin AC.$ Let the reflections of $P$ in the sidelines $BC, CA, AB$ be $P_1, P_2, P_3.$

Then the circumcenter $Q$ of the $\triangle P_1P_2P_3$ is the isogonal conjugate of $P.$

Points $A, B,$ and $C$ have not isogonal conjugate points.

Another points of sidelines $BC, AC, AB$ have points $A, B, C,$ respectively as isogonal conjugate points.

Proof $PC = P_1C, PC = P_2C \implies P_1C = P_2C.$ $\angle ACQ = \angle BCP_1 \implies \angle QCP_1 = \angle ACB.$ $\angle BCQ = \angle ACP_2 \implies \angle QCP_2 = \angle ACB.$ $\angle QCP_1 = \angle QCP_2, CP_1 = CP_2, QC$ is common therefore $\triangle QCP_1 = \triangle QCP_2 \implies QP_1 = QP_2.$ Similarly $QP_1 = QP_3 \implies Q$ is the circumcenter of the $\triangle P_1P_2P_3.$ $\blacksquare$

From definition 1 we get that $P$ is the isogonal conjugate of $Q.$

It is clear that each point $P$ has the unique isogonal conjugate point.

Let point $P$ be the point with barycentric coordinates $(p : q : r),$ $p = [(P - B),(P - C)], q = [(P - C),(P - A)], r = [(P - A),(P - B)].$ Then $Q$ has barycentric coordinates $(p' : q' : r'), p' = \frac {|B - C|^2}{p}, q' = \frac {|A-C|^2}{q}, r' = \frac {|A - B|^2}{r}.$

vladimir.shelomovskii@gmail.com, vvsss

Distance to the sides of the triangle

Let $Q$ be the isogonal conjugate of a point $P$ with respect to a triangle $\triangle ABC.$

Let $E$ and $D$ be the projection $P$ on sides $AC$ and $BC,$ respectively.

Let $E'$ and $D'$ be the projection $Q$ on sides $AC$ and $BC,$ respectively.

Then $\frac {PE}{PD} = \frac{QD'}{QE'}.$

Proof

Let $\theta = \angle ACP = \angle BCQ, \Theta = \angle ACQ = \angle BCP.$ $\frac {PE}{PD} = \frac {PC \sin \theta}{PC \sin \Theta} = \frac {QC \sin \theta}{QC \sin \Theta} = \frac {QD'}{QE'}. \blacksquare$ vladimir.shelomovskii@gmail.com, vvsss

Sign of isogonally conjugate points

Let triangle $\triangle ABC$ and points $P$ and $Q$ inside it be given.

Let $D, E, F$ be the projections $P$ on sides $BC, AC, AB,$ respectively.

Let $D', E', F'$ be the projections $Q$ on sides $BC, AC, AB,$ respectively.

Let $\frac {PE}{PD} = \frac{QD'}{QE'}, \frac {PF}{PD} = \frac{QD'}{QF'}.$ Prove that point $Q$ is the isogonal conjugate of a point $P$ with respect to a triangle $\triangle ABC.$

One can prove a similar theorem in the case $P$ outside $\triangle ABC.$

Proof

$\frac {PE}{PD} = \frac {PE}{PC} : \frac {PD}{PC} = \frac {\sin \angle ACP}{\sin \angle BCP},$ $\frac {QD'}{QE'} = \frac {QD'}{QC} : \frac {QE'}{QC} = \frac {\sin \angle BCQ}{\sin \angle ACQ}.$

Denote $\angle ACP = \varphi, \angle BCQ = \psi, \angle ACB = \gamma.$ $\sin \varphi \cdot \sin (\gamma - \psi) = \sin \psi \cdot \sin (\gamma - \varphi) \implies$ $\cos (\varphi - \gamma + \psi) - \cos(\varphi + \gamma - \psi) = \cos (\psi - \gamma + \varphi) - \cos(\psi + \gamma - \varphi)$ $\cos (\gamma + \varphi - \psi) = \cos(\gamma - \psi + \varphi) \implies$ $\cos \gamma \cos (\varphi - \psi) - \sin \gamma \sin (\varphi - \psi) = \cos \gamma \cos (\varphi - \psi) + \sin \gamma \sin (\varphi - \psi)$ $2 \sin \gamma \cdot \sin (\varphi - \psi) = 0, \varphi + \psi < 180^\circ \implies \varphi = \psi.$ Similarly $\angle ABP = \angle CBQ.$ Hence point $Q$ is the isogonal conjugate of a point $P$ with respect to a triangle $\triangle ABC. \blacksquare$

vladimir.shelomovskii@gmail.com, vvsss

Circumcircle of pedal triangles

Let $Q$ be the isogonal conjugate of a point $P$ with respect to a triangle $\triangle ABC.$

Let $E, D, F$ be the projection $P$ on sides $AC, BC, AB,$ respectively.

Let $E', D', F'$ be the projection $Q$ on sides $AC, BC, AB,$ respectively.

Prove that points $D, D', E, E', F, F'$ are concyclic.

The midpoint $PQ$ is circumcenter of $DD'EE'FF'.$

Proof

Let $\theta = \angle ACP = \angle BCQ, \Theta = \angle ACQ = \angle BCP.$ $CE \cdot CE' = PC \cos \theta \cdot QC \cos \Theta = PC \cos \Theta \cdot QC \cos \theta = CD \cdot CD'.$

Hence points $D, D', E, E'$ are concyclic.

$PQE'E$ is trapezoid, $E'E \perp PE \implies OE = OE' \implies$

the midpoint $PQ$ is circumcenter of $DD'EE'.$

Similarly points $D, D', F, F'$ are concyclic and points $F, F', E, E'$ are concyclic.

Therefore points $D, D', E, E', F, F'$ are concyclic, so the midpoint $PQ$ is circumcenter of $DD'EE'FF'.$

vladimir.shelomovskii@gmail.com, vvsss

Common circumcircle of the pedal triangles as the sign of isogonally conjugate points

Let triangle $\triangle ABC$ and points $P$ and $Q$ inside it be given. Let $D, E, F$ be the projections $P$ on sides $BC, AC, AB,$ respectively. Let $D', E', F'$ be the projections $Q$ on sides $BC, AC, AB,$ respectively.

Let points $D, E, F, D', E', F'$ be concyclic and none of them lies on the sidelines of $\triangle ABC.$

Then point $Q$ is the isogonal conjugate of a point $P$ with respect to a triangle $\triangle ABC.$

This follows from the uniqueness of the conjugate point and the fact that the line intersects the circle in at most two points.

vladimir.shelomovskii@gmail.com, vvsss

Two pares of isogonally conjugate points

Let triangle $\triangle ABC$ and points $X$ and $Y$ be given. Let points $X'$ and $Y'$ be the isogonal conjugate of a points $X$ and $Y$ with respect to a triangle $\triangle ABC,$ respectively.

Let $XY$ cross $X'Y'$ at $Z$ and $XY'$ cross $X'Y$ at $Z'.$

Prove that point $Z'$ is the isogonal conjugate of a point $Z$ with respect to $\triangle ABC.$

Proof

There are two pairs of isogonals $CX - CX'$ and $CY - CY'$ with respect to the angle $\angle ACB \implies$ $CZ - CZ'$ are isogonals with respect to the $\angle ACB$ in accordance with The isogonal theorem.

Similarly $AZ - AZ'$ are the isogonals with respect to the $\angle BAC.$

Therefore the point $Z'$ is the isogonal conjugate of a point $Z$ with respect to $\triangle ABC.$

vladimir.shelomovskii@gmail.com, vvsss

Circles

Let $Q$ be the isogonal conjugate of a point $P$ with respect to a triangle $\triangle ABC.$

Let $D$ be the circumcenter of $\triangle BCP.$

Let $E$ be the circumcenter of $\triangle BCQ.$

Prove that points $D$ and $E$ are inverses with respect to the circumcircle of $\triangle ABC.$

Proof

The circumcenter of $\triangle ABC$ point $O,$ and points $D$ and $E$ lies on the perpendicular bisector of $BC.$ $\angle BOD = \angle COE = \angle BAC.$ $2 \angle BDO = \angle BDC = \overset{\Large\frown} {BC} =$ $= 360^\circ - \overset{\Large\frown} {CB} = 360^\circ - 2 \angle BPC.$ $\angle BDO = 180^\circ - \angle BPC = \angle PBC + \angle PCB.$ Similarly $\angle CEO = 180^\circ - \angle BQC = \angle QBC + \angle QCB.$ $\angle PBC + \angle QBC = \angle PBC + \angle PBA = \angle ABC.$ $\angle QCB + \angle PCB = \angle QCB + \angle QCA = \angle ACB.$

$\angle CEO +\angle BDO = \angle ABC + \angle ACB = 180^\circ - \angle BAC \implies$ $\angle OBD = 180^\circ - \angle BOD - \angle BDO = \angle OEC \implies$ $\triangle OBD \sim \triangle OEC \implies \frac {OB}{OE} = \frac {OD}{OC} \implies OD \cdot OE = OB^2. \blacksquare$

vladimir.shelomovskii@gmail.com, vvsss

Equidistant isogonal conjugate points

Let triangle $ABC$ with incenter $I$ be given. Denote $\omega = \odot BIC.$

Let point $P'$ be the isogonal conjugate of the point $P$ with respect to $\triangle ABC.$

Prove that $AP = AP'$ iff $P \in \omega.$

Proof

1. Let $P \in \omega.$ WLOG, $P \in \angle BAI.$ Point $P \in \omega \implies \angle PBI = \angle PCI.$

Point $P'$ is the isogonal conjugate of the point $P$ with respect to $\triangle ABC \implies$ $\angle PBI = \angle P'BI, \angle PCI = \angle P'CI \implies \angle P'BI = \angle P'CI.$ So points $B,C,I, P,$ and $P'$ are concyclic.

Let $E = AI \cap \odot ABC.$ Then $E$ is the center of $\omega \implies$ $EP = EP', \angle IEP = \angle IEP' = 2 \angle PBI.$ $\triangle AEP = \triangle AEP' \implies AP = AP'.$

2. Let $AP = AP'.$ $\angle PAI = \angle PAE = \angle P'AI = \angle P'AE \implies$

Points $P$ and $P'$ are symmetric with respect $AI \implies PE = P'E.$

Suppose that $P \notin \odot BIC.$

Let $O$ be the center of $\odot BPC, O'$ be the center of $\odot BP'C.$

It is known that points $O$ and $O'$ are inverted with respect to the circumcircle of $\triangle ABC.$

Points $O, O',$ and $E$ belong to bisector $BC, E \in \odot ABC.$

Therefore $\overset{\Large\frown} {BIC}$ divide $\overset{\Large\frown} {BPC}$ and $\overset{\Large\frown} {BP'C}.$

WLOG (see diagram) $PE > IE > P'E,$ contradiction.

vladimir.shelomovskii@gmail.com, vvsss

Simplified distance formula for isogonal points

Let triangle $\triangle ABC,$ points $P$ and $P',$ and $\odot ABC = \Omega$ be given. Let point $P'$ be the isogonal conjugate of a point $P$ with respect to a triangle $\triangle ABC.$ $D = AP \cap BC, E = AP' \cap BC, F = AP \cap \Omega, G = AP' \cap \Omega.$ Prove that $PF \cdot P'G= AF \cdot EG.$

Proof

$\angle AFC$ and $\angle AGC$ are both subtended by arc $\overset{\Large\frown} {AC} \implies \angle AFC = \angle AGC.$ $\angle PCF = \angle PCB + \angle BCF = \angle P'CA + \angle BAF = \angle P'CA + \angle P'AC=$ $= \angle GP'C \implies \triangle CPF \sim \triangle P'CG \implies PF \cdot P'G = FC \cdot CG.$ Similarly $\triangle CAF \sim \triangle ECG \implies AF \cdot EG = FC \cdot CG.$ Product of isogonal segments

vladimir.shelomovskii@gmail.com, vvsss

Point on circumcircle

Let triangle $\triangle ABC,$ points $D \in BC$ and $E \in BC$ be given.

Denote $\Omega = \odot ABC, \omega = \odot AED, G = \omega \cap \Omega \ne A, F = AG \cap BC,$ $K = AE \cap \Omega \ne A, L = GD \cap \Omega \ne G.$ Prove that $KL || BC.$

Proof

WLOG, the order of the points is $B,E,F,C,D,$ as shown on diagram.

The spiral symilarity centered at $A$ maps $\Omega$ to $\omega$ and point $L \in \Omega$ to point $D \in \omega \implies \overset{\Large\frown} {AL} = \overset{\Large\frown} {AD} \implies \angle ABL = \angle AED.$

$\angle AED$ is the external angle of $\triangle AEB \implies \angle AED = \angle ABC + \angle BAE \implies$ $\angle CBL = \angle BAK \implies \overset{\Large\frown} {BK} = \overset{\Large\frown} {CL} \implies BC ||KL. \blacksquare$

Corollary

$AL$ is the isogonal conjugate to $AK$ with respect $\angle BAC.$

vladimir.shelomovskii@gmail.com, vvsss

Fixed point on circumcircle

Let triangle $\triangle ABC,$ point $G \ne A$ on circumcircle $\Omega = \odot ABC,$ and point $D \in BC$ be given.

Point $P$ lies on $AG,$ point $P'$ be the isogonal conjugate of a point $P$ with respect to a triangle $\triangle ABC, Q = DP' \cap AP, F = \odot DPQ \cap \Omega.$

Prove that $F$ is fixed point and not depends from position of $P.$

Proof

WLOG, the order of points on sideline is $B, C, D,$ point $B$ is closer to $AP$ than to $AP'.$

Denote $Y = AP \cap BC, Z = AP' \cap BC,\omega = \odot ADY,$ $F' = \omega \cap \Omega \ne A, H = \Omega \cap F'D \ne F'.$

Spiral similarity centered at $A$ which maps $\Omega$ into $\odot AYD$ transform point $H$ into point $D \implies$ $\overset{\Large\frown} {ACH} = \overset{\Large\frown} {AD} \implies \angle AGH = \angle AYD \implies GH||BC \implies$ $\overset{\Large\frown} {CH} = \overset{\Large\frown} {BG} \implies \angle BAG = \angle CAH \implies H \in AP'.$ Points $F', H,$ and $D$ are collinear.

It is known ( Ratio of isogonal segments) that $\frac {AP'}{P'Z} \cdot \frac {AP}{PY} = \frac {AH}{HZ}.$

We use the ratio of the areas and get: $\frac {[AQD]}{[QYD]} = \frac{AQ}{QY}, \frac {[ZQD]}{[YQD]} = \frac{ZD}{YD},$ $\frac {[AQD]}{[ZQD]} = \frac{AP'}{P'Z} \implies$ $\frac{AQ}{QY} = \frac {[AQD]}{[QYD]} = \frac {[AQD]}{[ZQD]} \cdot \frac {[ZQD]}{[YQD]} = \frac{AP'}{P'Z} \cdot \frac{ZD}{YD}.$ Denote $X = AP \cap DH.$ $\frac {[AXD]}{[YXD]} = \frac{AX}{XY}, \frac {[XZD]}{[XYD]} = \frac{ZD}{YD},$ $\frac {[AXD]}{[XZD]} = \frac{AH}{HZ} \implies$ $\frac{AX}{XY} = \frac {[AXD]}{[YXD]} = \frac {[AXD]}{[XZD]} \cdot \frac {[XZD]}{[YXD]} = \frac{AH}{HZ} \cdot \frac{ZD}{YD}.$ Therefore $\frac{AX}{XY} = \frac{AQ}{QY} \cdot \frac{AP}{PY}$ which means ( Problems | Simple) that $DX$ is the radical axes of $\omega$ and $\odot DPQ \implies$

$F = F'$ and not depends from position of $P.$

Fixed point on circumcircle

vladimir.shelomovskii@gmail.com, vvsss

Distance formula for isogonal points

Let triangle $\triangle ABC$ and point $P$ be given.

Let point $P'$ be the isogonal conjugate of a point $P$ with respect to a triangle $\triangle ABC.$

Let lines $AP$ and $AP'$ cross sideline $BC$ at $D$ and $E$ and circumcircle of $\triangle ABC$ at $F$ and $G,$ respectively.

We apply the Isogonal’s property and get $\frac {BD}{DC} \cdot \frac{BE}{EC} = \frac {AB^2}{AC^2}.$

$EF || BC.$ We apply the Ptolemy's theorem to $BCGF$ and get $BC \cdot FG = BG^2 – BF^2.$

We apply the barycentric coordinates and get $\left| \frac{BE}{EC} - \frac {BD}{DC} \right| = \frac {AB \cdot BC \cdot FG}{AC \cdot PF \cdot P'G}.$

Barycentric coordinates

vladimir.shelomovskii@gmail.com, vvsss

Miquel point for isogonal conjugate points

Let triangle $\triangle ABC,$ points $Q \in BC$ and $P$ be given. Let point $P'$ be the isogonal conjugate of a point $P$ with respect to a triangle $\triangle ABC.$ $D = QP \cap AP', E = AP \cap QP'.$ Let $M$ be the Miquel point of a complete quadrilateral $PDP'E.$

Prove that $M$ lies on the circumcircle of $\triangle ABC.$

Proof

Point $A$ is the isogonal conjugate of a point $Q$ with respect to a triangle $\triangle ABC,$ so point $D$ is the isogonal conjugate of a point $E$ with respect to a triangle $\triangle ABC.$

Points $P$ and $E$ lies on the same line, therefore $PF \cdot P'G = EF \cdot DG \implies$

$\frac {PF-EP}{PF} = \frac{DG-DP'}{DG} \implies \frac {EP}{PF} = \frac{DP'}{DG}.$ Point $M$ lies on circles $APD$ and $AEP' \implies$ spiral similarity centered at $M$ transform triangle $\triangle MPE$ to $\triangle MDP' \implies$ $\angle MPE = \angle MDP', \frac {MP}{MD} = \frac {PE}{DP'} = \frac{PF}{DG} \implies$ $\triangle MPF \sim \triangle MDG \implies$ $\angle AFM = \angle AGM \implies M \in \odot ABC.$

vladimir.shelomovskii@gmail.com, vvsss

Point on circumcircle

Let triangle $\triangle ABC,$ and points $D \in BC$ and $E \in \odot ABC = \Omega$ be given.

Let $\odot ADE = \omega, F = BC \cap \omega \ne D.$

Let lines $AF$ and $AG (G \in BC)$ be the isogonals with respect to the angle $\angle BAC, \odot AGD = \theta.$

Let $P$ be an arbitrary point on $AF, Q = DP \cap AG, H = \theta \cap \Omega.$

Prove that $X = EP \cap HQ$ lies on $\Omega.$

Simplified problem

Let $\triangle ABC,$ and points $D \in BC$ and $E \in \odot ABC = \Omega$ be given, $\omega = \odot ADE, F = \omega \cap BC \ne D.$

Let lines $AF$ and $AG (G \in BC)$ be the isogonals with respect to $\angle BAC, \theta = \odot AGD, H = \theta \cap \Omega.$

Prove that $X = EF \cap HG \in \Omega.$

Proof, Simplified problem $\angle CGH = \angle DAH = \frac{1}{2} \overset{\Large\frown} {HD} (\theta),$ $\angle DFE = \angle DAE = \frac{1}{2} \overset{\Large\frown} {ED} (\omega),$ $\angle EAH = \angle DAE - \angle DAH = \frac{1}{2} \overset{\Large\frown} {EH}(\Omega),$ $\angle EXH = \angle DFE - \angle DGH = \angle EAH \implies$

points $A, H, E, X$ are concyclic on $\Omega.$

Proof

Let points $P'$ and $Q'$ be the isogonal conjugate of a points $P$ and $Q$ with respect to a triangle $\triangle ABC, \omega' = \odot Q'PD, \theta' = \odot P'QD.$

It is known that $E \in \omega', H \in \theta', \omega' \cap \theta' \cap \Omega = M.$

$\angle DQH = \angle DMH = \frac{1}{2} \overset{\Large\frown} {HD} (\theta'),$ $\angle DPE = \angle DME = \frac{1}{2} \overset{\Large\frown} {ED} (\omega'),$ $\angle EMH = \angle DME - \angle DMH = \frac{1}{2} \overset{\Large\frown} {EH}(\Omega),$ $\angle EXH = \angle DPE - \angle DQH = \angle EMH \implies$ points $M, H, E, X$ are concyclic on $\Omega.$

vladimir.shelomovskii@gmail.com, vvsss

Isogonal of line BC with respect to angle BAC

Let triangle $\triangle ABC$ be given, $\Omega = \odot ABC, AD || BC.$

Let lines $AE$ and $AD$ be the isogonals with respect to $\angle BAC.$

Prove that $AE$ is tangent to $\Omega.$

Proof

Let $O$ and $H$ be the circumcenter and the orthocenter of $\triangle ABC,$ respectively. $AH \perp BC, AD || BC \implies AH \perp AD.$ $AH$ is isogonal to $AO$ with respect to $\angle BAC \implies AE \perp AO \implies AE$ is tangent to $\Omega.$

vladimir.shelomovskii@gmail.com, vvsss

Isogonal bijection lines and points

Let triangle $\triangle ABC$ and line $\ell, P \in \ell$ be given, $\Omega = \odot ABC.$

Define $G \in \Omega$ the point with property $G' \in \ell.$

Prove that $\angle ABG$ is equal the angle $\theta$ between $\ell$ and $BC.$

Proof

WLOG, the configuration is the same as shown on diagram, $F = \ell \cap BC, AD' || \ell, \theta = \angle PFB, AD || BC, AE$ is the tangent to $\Omega.$

$AD$ is isogonal to $AE, AD'$ is isogonal to $AG$ with respect to $\angle BAC \implies$ $\theta = \angle PFB = \angle D'AD = \angle GAE = \angle GBA.$ A bijection has been established between the set of lines parallel to a given one and the set of points of the circumcircle.

vladimir.shelomovskii@gmail.com, vvsss

Miquel point for two pare isogonal points

Let triangle $\triangle ABC$ and points $P$ and $Q$ be given.

Let points $P'$ and $Q'$ be the isogonal conjugate of the points $P$ and $Q$ with respect to $\triangle ABC, \Omega = \odot ABC, M$ is the Miquel point of quadrilateral $PQP'Q'.$

Prove that $M \in \Omega.$

Proof

Denote $R = PQ \cap P'Q', \Theta = \odot P'QR, \theta = \odot PQ'R.$

Then $M = \theta \cap \Theta$ is the Miquel point of quadrilateral $PQP'Q'.$

Denote $E = \theta \cap \Omega \notin \Theta, F = \Theta \cap \Omega \notin \theta.$

Let $D \in \Omega$ be the point with property $D' \in PQ.$

WLOG, configuration is similar as shown in diagram.

$P' \in DF, Q' \in DE$ ( Isogonal_bijection_lines_and_points). $\angle EMF = \angle RME - \angle RMF = \angle RQ'E - \angle RP'F = \angle P'Q'E - \angle DP'Q' = \angle P'DQ' = \angle EDF \implies M \in \odot DEF \blacksquare$

vladimir.shelomovskii@gmail.com, vvsss

Isogonic center’s conjugate point

Let triangle $ABC$ with isogonic center $F (X(13)$ or $X(14))$ be given. Denote $\omega = \odot BIC.$

Let line $\ell_A$ be the axial symmetry of line $AF$ according to the sideline $BC.$

Define lines $\ell_B$ and $\ell_C$ similarly.

Prove that the lines $\ell_A, \ell_B,$ and $\ell_C$ are concurrent.

Proof

Let $I$ be the incenter of $\triangle ABC, F =X(13).$ $A_1 = AF \cup BC, E = AI \cup BC, D \in BC, AD \perp AE, \omega = \odot AED.$ Let $F_1 = AF \cup \omega, F'$ is simmetric to $F_1$ with respect $BC \implies A_1F' = \ell_A.$

The diameter $DE$ of $\omega$ lies on $BC \implies F_1 \in \omega, \overset{\Large\frown} {EF_1} = \overset{\Large\frown} {EF'} \implies \angle EAF_1 = \angle EAF'.$

Therefore $AF'$ is the isogonal conjugate of $AF$ with respect to $\angle BAC.$

Similarly $\ell_B$ and $\ell_C$ are the isogonal conjugate of $BF$ and $CF,$ so point $F'$ is the isogonal conjugate of point $F$ with respect to $\triangle ABC.$

The second diagram show construction in the case $F =X(14).$ The proof is similar.

vladimir.shelomovskii@gmail.com, vvsss

Three pairs isogonal points

Let a triangle $ABC,$ points $D$ and $E \in AD$ be given, $F = CD \cap BE.$ Points $D', E'$ and $F'$ are the isogonal conjugate of the points $D, E,$ and $F,$ respectively, with respect to $\triangle ABC.$

Prove that $\frac {AD}{AE} \cdot \frac {BE}{BF} \cdot \frac {CF}{CD} = \frac {AE'}{AD'} \cdot \frac {BF'}{BE'} \cdot \frac {CD'}{CF'}.$

Proof

Denote $\angle BAC = \alpha, \angle ABC = \beta, \angle ACB = \gamma,$ $\angle BAD = \varphi_A, \angle CBE = \varphi_B, \angle ACD = \varphi_C.$ We use isogonal properties and get $\angle CAD' = \varphi_A, \angle ABE' = \varphi_B, \angle BCD' = \varphi_C.$ By applying the Law of Sines, we get $\frac {BE}{AE} = \frac {\sin \varphi_A}{\sin (\beta - \varphi_B)}, \frac {CF}{BF} = \frac {\sin \varphi_B}{\sin (\gamma - \varphi_C)}, \frac {AD}{CD} = \frac {\sin \varphi_C}{\sin (\alpha - \varphi_A)}.$ Symilarly, $\frac {AE'}{BE'} = \frac {\sin \varphi_B}{\sin (\alpha - \varphi_A)}, \frac {BF'}{CF'} = \frac {\sin \varphi_C}{\sin (\beta - \varphi_B)}, \frac {CD'}{AD'} = \frac {\sin \varphi_A}{\sin (\gamma - \varphi_C)}.$ We multiply these equations and get $\frac {AE \cdot BF \cdot CD}{AD \cdot BE \cdot CF} = \frac{AD' \cdot BE' \cdot CF'}{AE' \cdot BF' \cdot CD'} = \frac {\sin \varphi_A \cdot \sin \varphi_B \cdot \sin \varphi_C}{\sin (\alpha - \varphi_A) \cdot \sin (\beta - \varphi_B) \cdot \sin (\gamma - \varphi_C)}.$ vladimir.shelomovskii@gmail.com, vvsss

Ratio for three pairs of isogonal points

Let a triangle $ABC,$ points $D$ and $E \in AD$ be given, $F = CD \cap BE.$

Points $D', E'$ and $F'$ are the isogonal conjugate of the points $D, E,$ and $F,$ respectively, with respect to $\triangle ABC.$

Denote $R$ and $R'$ the circumradii of triangles $\triangle DEF$ and $\triangle D'E'F',$ respectively.

Prove that $\frac {AD \cdot BE \cdot CF}{R} = \frac {AE' \cdot BF' \cdot CD'}{R'}.$

Proof

Denote $\frac {AD}{DE} = u, \frac {BE}{EF} = w, \frac {CF}{FD} = v.$

$[DEF] = 1,$ where $[X]$ is the area of the figure $X.$ $\frac {[ADF]}{[DEF]} = \frac {AD}{DE} = u, \frac {[ACF]}{[DEF]} = \frac {[ACF]}{[ADF]} \cdot \frac {[ADF]}{[DEF]} = uv.$ Similarly, $\frac {[CFE]}{[DEF]} = v, \frac {[BCE]}{[DEF]} = vw, \frac {[BDE]}{[DEF]} = w, \frac {[ABD]}{[DEF]} = uw.$ $\frac {[ABC]}{[DEF]} = 1 + u + v + w + uv + uw + vw = (1 + u)(1 + v)(1 + w) - uvw,$ $\frac {[ABC]}{[DEF]} = \frac {AE \cdot BF \cdot CD}{DE \cdot DF \cdot EF} - \frac {AD \cdot BE \cdot CF}{DE \cdot DF \cdot EF}.$ $\frac {DE \cdot DF \cdot EF}{4R} = [DEF] \implies$ $[ABC] = \frac {AD \cdot BE \cdot CF}{4R} \cdot \left ( \frac {AE \cdot BF \cdot CD}{BE \cdot CF \cdot AD}-1 \right).$ Similarly, $[ABC] = \frac {AE' \cdot BF' \cdot CD'}{4R'} \cdot \left ( \frac {AD' \cdot BE' \cdot CD}{AE' \cdot BF' \cdot CD'}-1 \right).$ It is known that $\frac {AD}{AE} \cdot \frac {BE}{BF} \cdot \frac {CF}{CD} = \frac {AE'}{AD'} \cdot \frac {BF'}{BE'} \cdot \frac {CD'}{CF'}$ ( Three pairs isogonal points), therefore $\frac {AD \cdot BE \cdot CF}{4R} = \frac {AE' \cdot BF' \cdot CD'}{4R'}.$ Comment: The main idea of the proof was found by Leonid Shatunov.

vladimir.shelomovskii@gmail.com, vvsss

Problems

Given a nonisosceles, nonright triangle $ABC,$ let $O$ denote the center of its circumscribed circle, and let $A_1, \, B_1,$ and $C_1$ be the midpoints of sides $BC, \, CA,$ and $AB,$ respectively. Point $A_2$ is located on the ray $OA_1$ so that $\triangle OAA_1$ is similar to $\triangle OA_2A$ . Points $B_2$ and $C_2$ on rays $OB_1$ and $OC_1,$ respectively, are defined similarly. Prove that lines $AA_2, \, BB_2,$ and $CC_2$ are concurrent. (Source)

Let $P$ be a given point inside quadrilateral $ABCD$ . Points $Q_1$ and $Q_2$ are located within $ABCD$ such that $\angle Q_1 BC = \angle ABP$ , $\angle Q_1 CB = \angle DCP$ , $\angle Q_2 AD = \angle BAP$ , $\angle Q_2 DA = \angle CDP$ . Prove that $\overline{Q_1 Q_2} \parallel \overline{AB}$ if and only if $\overline{Q_1 Q_2} \parallel \overline{CD}$ . (Source)

Let $AA', BB',$ and $CC'$ be the bisectors of a triangle $\triangle ABC.$

The segments $BB'$ and $A'C'$ meet at point $D.$ Let $E$ be the projection of $D$ to $AC.$

Points $P$ and $Q$ on the sides $AB$ and $BC,$ respectively, are such that $EP = PD, EQ = QD.$

Prove that $\angle PDB' = \angle EDQ.$ (Source)

IMO 2007 Short list/G3

The diagonals of a trapezoid $ABCD$ intersect at point $P.$

Point $Q$ lies between the parallel lines $BC$ and $AD$ such that $\angle AQD = \angle CQB,$ and line $CD$ separates points $P$ and $Q.$

Prove that $\angle BQP = \angle DAQ.$

Proof

$\angle AQD = \angle CQB \implies$

$BQ$ and $AQ$ are isogonals with respect $\angle CQD.$

$P =AC \cap BD, BC || AD \implies$

$QS || AD$ is isogonal to $QP$ with respect $\angle CQD.$

From the converse of The isogonal theorem we get

$\angle BQP = \angle SQA = \angle DAQ \blacksquare$

vladimir.shelomovskii@gmail.com, vvsss

This article is a stub. Help us out by expanding it.

@@ Line 1: / Line 1: @@
 '''Isogonal conjugates''' are pairs of [[point]]s in the [[plane]] with respect to a certain [[triangle]].
+== The isogonal theorem ==
+=== Isogonal lines definition ===
+Let a line <math>\ell</math> and a point <math>O</math> lying on <math>\ell</math>  be given. A pair of lines symmetric with respect to <math>\ell</math>  and containing the point <math>O</math> be called isogonals with respect to the pair <math>(\ell,O).</math>
+Sometimes it is convenient to take one pair of isogonals as the base one, for example, <math>OA</math> and <math>OB</math> are the base pair. Then we call the remaining pairs as isogonals with respect to the angle <math>\angle AOB.</math>
+=== Projective transformation ===
+It is known that the transformation that maps a point with coordinates <math>(x,y)</math> into a point with coordinates <math>(\frac{1}{x}, \frac {y}{x}),</math> is projective.
+If the abscissa axis coincides with the line <math>\ell</math> and the origin coincides with the point <math>O,</math> then the isogonals define the equations <math>y = \pm kx,</math> and the lines <math>(\frac{1}{x}, \pm k)</math> symmetrical with respect to the line <math>\ell</math> become their images.
+It is clear that, under the converse transformation (also projective), such pairs of lines become isogonals, and the points equidistant from <math>\ell</math> lie on the isogonals.
+=== The isogonal theorem ===
+[[File:Isogonal.png|390px|right]]
+Let two pairs of isogonals <math>OX - OX'</math> and <math>OY - OY'</math> with respect to the pair <math>(\ell,O)</math> be given. Denote <math>Z = XY \cap X'Y', Z' = X'Y \cap XY'.</math>
+Prove that <math>OZ</math> and <math>OZ'</math> are the isogonals with respect to the pair <math>(\ell,O).</math>
+==== Proof ====
+[[File:Transform isogonal.png|390px|right]]
+Let us perform a projective transformation of the plane that maps the point <math>O</math> into a point at infinity and the line <math>\ell</math> maps to itself. In this case, the isogonals turn into a pair of straight lines parallel to <math>\ell</math> and equidistant from <math>\ell.</math>
+The converse (also projective) transformation maps the points equidistant from <math>\ell</math> onto isogonals. We denote the image and the preimage with the same symbols.
+Let the images of isogonals are vertical lines. Let coordinates of images of points be <cmath>X(-a, 0), X'(a,u), Y(-b,v), Y'(b,w).</cmath>
+Equation of a straight line <math>XY</math> is <math>\frac{x + a}{a - b} = \frac {y}{v}.</math>
+Equation of a straight line <math>X'Y'</math> is <math>\frac{x - a}{b - a} = \frac {y - u}{w - u}.</math>
+The abscissa <math>Z_x</math> of the point <math>Z</math> is <math>Z_x = \frac {v a - a w + u b}{u - v - w}.</math>
+Equation of a straight line <math>XY'</math> is <math>\frac{x + a}{b + a} = \frac {y}{w}.</math>
+Equation of a straight line <math>X'Y</math> is <math>\frac{x - a}{- b - a} = \frac {y - u}{v - u}.</math>
+The abscissa <math>Z'_x</math> of the point <math>Z'</math> is <math>Z'_x = \frac {v a - a w + u b}{- u + v + w} = - Z_x \implies</math>
+Preimages of the points <math>Z</math> and <math>Z'</math> lie on the isogonals. <math>\blacksquare</math>
+=== The isogonal theorem in the case of parallel lines ===
+[[File:Parallels 1.png|330px|right]]
+Let <math>OY</math> and <math>OY'</math> are isogonals with respect <math>\angle XOX'.</math>
+Let lines <math>XY</math> and <math>X'Y'</math> intersect at point <math>Z, X'Y || XY'.</math>
+Prove that <math>OZ</math> and line <math>l</math> through <math>O</math> parallel to <math>XY'</math> are the isogonals with respect <math>\angle XOX'.</math>
+==== Proof ====
+The preimage of <math>Z'</math> is located at infinity on the line <math>l.</math>
+The equality <math>Z'_x = -Z_x</math> implies the equality the slopes modulo of <math>OZ</math> and <math>l</math> to the bisector of <math>\angle XOX'. \blacksquare</math>
+=== Converse theorem ===
+[[File:Parallels 2.png|390px|right]]
+Let lines <math>XY</math> and <math>X'Y'</math> intersect at point <math>Z, X'Y || XY'.</math>
+Let <math>OZ</math> and <math>l</math> be the isogonals with respect <math>\angle XOX'.</math>
+Prove that <math>OY</math> and <math>OY'</math> are isogonals with respect <math>\angle XOX' (\angle XOY' = \angle YOX').</math>
+==== Proof ====
+The preimage of <math>Z'</math> is located at infinity on the line <math>l,</math> so the slope of <math>OZ</math> is known.
+Suppose that <math>y' \in XY', y' \ne Y', \angle y'OX = \angle YOX'.</math>
+The segment <math>XY</math> and the lines <math>XY', OZ</math> are fixed <math>\implies</math>
+<math>y'X'</math> intersects <math>XY</math> at <math>z \ne Z,</math>
+but there is the only point where line <math>OZ</math> intersect <math>XY.</math> Сontradiction. <math>\blacksquare</math>
+'''vladimir.shelomovskii@gmail.com, vvsss'''
+==Parallel segments==
+[[File:Parallels.png|350px|right]]
+Let triangle <math>ABC</math> be given. Let <math>AD</math> and <math>AE</math> be the isogonals with respect <math>\angle BAC.</math> Let <math>BD ||CE, P = BE \cap CD.</math>
+Prove that <math>P</math> lies on bisector of <math>\angle BAC</math> and <math>BD||AP.</math>
+<i><b>Proof</b></i>
+Both assertions follow from <i><b>The isogonal theorem in the case of parallel lines</b></i>
+'''vladimir.shelomovskii@gmail.com, vvsss'''
+==Perpendicularity==
+[[File:Right angles.png|400px|right]]
+Let triangle <math>ABC</math> be given. Right triangles <math>ABD</math> and <math>ACE</math> with hypotenuses <math>AD</math> and <math>AE</math> are constructed on sides <math>AB</math> and <math>AC</math> to the outer (inner) side of <math>\triangle ABC.</math> Let <math>\angle BAD = \angle CAE, H = CD \cap BE.</math>
+Prove that <math>AH \perp BC.</math>
+<i><b>Proof</b></i>
+Let <math>\ell</math> be the bisector of <math>\angle BAC, F = BD \cap CE.</math>
+<math>AB</math> and <math>AC</math> are isogonals with respect to the pair <math>(\ell,A).</math>
+<math>AD</math> and <math>AE</math> are isogonals with respect to the pair <math>(\ell,A) \implies</math>
+<math>AH</math> and <math>AF</math> are isogonals with respect to the pair <math>(\ell,A)</math> in accordance with <i><b>The isogonal theorem.</b></i>
+<math>\angle ABD = \angle ACE = 90^\circ \implies</math>
+<math>AF</math> is the diameter of circumcircle of <math>\triangle ABC.</math>
+Circumradius and altitude are isogonals with respect bisector and vertex of triangle, so <math>AH \perp BC.</math> <math>\blacksquare</math>
+*[[Circumradius]]
+'''vvsss'''
+==Fixed point==
+[[File:Fixed point.png|400px|right]]
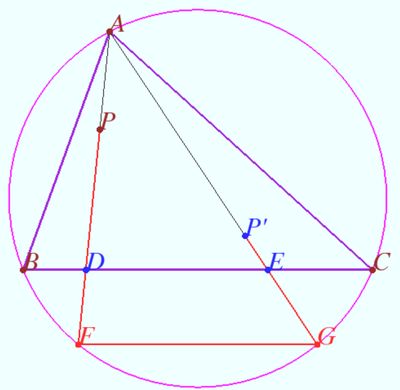
+Let fixed triangle <math>ABC</math> be given. Let points <math>D</math> and <math>E</math> on sidelines <math>BC</math> and <math>AB,</math> respectively be the arbitrary points.
+Let <math>F</math> be the point on sideline <math>AC</math> such that <math>\angle BDE = \angle CDF.</math>
+<math>G = BF \cap CE.</math> Prove that line <math>DG</math> pass through the fixed point.
+<i><b>Proof</b></i>
+We will prove that point <math>A',</math> symmetric <math>A</math> with respect <math>\ell = BC,</math> lies on <math>DG</math>.
+<math>\angle BDE = \angle CDF \implies DE</math> and <math>DF</math> are isogonals with respect to <math>(\ell, D).</math>
+<math>A = BE \cap CF \implies </math> points <math>A</math> and <math>G</math> lie on isogonals with respect to <math>(\ell, D)</math> in accordance with <i><b>The isogonal theorem.</b></i>
+Point <math>A'</math> symmetric <math>A</math> with respect <math>\ell</math> lies on isogonal <math>AD</math> with respect to <math>(\ell, D),</math> that is <math>DG.</math> <math>\blacksquare</math>
+'''vvsss'''
+==Bisector==
+[[File:Incircles.png|400px|right]]
+Let a convex quadrilateral <math>ABCD</math> be given. Let <math>I</math> and <math>J</math> be the incenters of triangles <math>\triangle ABC</math> and <math>\triangle ADC,</math> respectively.
+Let <math>I'</math> and <math>J'</math> be the A-excenters of triangles <math>\triangle ABC</math> and <math>\triangle ADC,</math> respectively. <math>E = IJ' \cap I'J.</math>
+Prove that <math>CE</math> is the bisector of <math>\angle BCD.</math>
+<i><b>Proof</b></i>
+<math>\angle ICI' = \angle JCJ' = 90^\circ \implies</math>
+<math>CI'</math> and <math>CJ'</math> are isogonals with respect to the angle <math>\angle ICJ.</math>
+<math>A = II' \cap JJ' \implies AC</math> and <math>EC</math> are isogonals with respect to the angle <math>\angle ICJ</math> in accordance with <i><b>The isogonal theorem.</b></i>
+Denote <math>\angle ACI = \angle BCI = \alpha, \angle ACJ = \angle DCJ = \beta.</math>
+WLOG, <math>\beta \ge \alpha.</math>
+<cmath>\angle ACJ = \angle ACE + \alpha = \beta,</cmath>
+<cmath>\angle BCE = 2 \alpha + \beta - \alpha = \alpha + \beta = \angle DCE. \blacksquare</cmath>
+'''vvsss'''
+==Isogonal of the diagonal of a quadrilateral==
+[[File:Quadrungle isogonals.png|250px|right]]
+Given a quadrilateral <math>ABCD</math> and a point <math>P</math> on its diagonal such that <math>\angle APB = \angle APD.</math>
+Let <math>E = AB \cap CD, F = AD \cap BC.</math>
+Prove that <math>\angle BPE = \angle DPF.</math>
+<i><b>Proof</b></i>
+[[File:Quadrungle transform.png|250px|right]]
+Let us perform a projective transformation of the plane that maps the point <math>P</math> to a point at infinity and the line <math>\ell = AC</math> into itself.
+In this case, the images of points <math>B</math> and <math>D</math> are equidistant from the image of <math>AC \implies</math>
+the point <math>M</math> (midpoint of <math>BD)</math> lies on <math>\ell \implies</math>
+<math>AC</math> contains the midpoints of <math>AC</math> and <math>BD \implies</math>
+<math>\ell</math> is the Gauss line of the complete quadrilateral <math>ABCDEF \implies</math>
+<math>\ell</math> bisects <math>EF \implies EE_0 = FF_0 \implies</math>
+the preimages of the points <math>E</math> and <math>F</math> lie on the isogonals <math>PE</math> and <math>PF. \blacksquare</math>
+'''vvsss'''
+==Isogonals in trapezium==
+[[File:Trapezium ACFEE.png|370px|right]]
+Let the trapezoid <math>AEFC, AC||EF,</math> be given. Denote <cmath>B = AE \cap CF, D = AF \cap CE.</cmath>
+The point <math>M</math> on the smaller base <math>AC</math> is such that <math>EM = MF.</math>
+Prove that <math>\angle AMB = \angle AMD.</math>
+<i><b>Proof</b></i>
+<cmath>EM = MF \implies </cmath>
+<cmath>\angle AME = \angle MEF = \angle MFE = \angle CMF.</cmath>
+Therefore <math>EM</math> and <math>FM</math> are isogonals with respect <math>(AC,M).</math>
+Let us perform a projective transformation of the plane that maps the point <math>M</math> to a point at infinity and the line <math>\ell = AC</math> into itself.
+In this case, the images of points <math>E</math> and <math>F</math> are equidistant from the image of <math>\ell \implies AC</math> contains the midpoints of <math>AC</math> and <math>EF</math>, that is, <math>\ell</math> is the Gauss line of the complete quadrilateral <math>ABCDEF \implies</math>
+<math>\ell</math> bisects <math>BD \implies BB_0 = DD_0 \implies</math>
+The preimages of the points <math>B</math> and <math>D</math> lie on the isogonals <math>MB</math> and <math>MD. \blacksquare</math>
+'''vvsss'''
+==Isogonals in complete quadrilateral==
+[[File:Isogonals in complete quadrilateral.png|400px|right]]
+Let complete quadrilateral <math>ABCDEF (E = AB \cap CD, F = AC \cap BD)</math> be given. Let <math>M</math> be the Miquel point of <math>ABCD.</math>
+Prove that <math>AM</math> is isogonal to <math>DM</math> and <math>EM</math> is isogonal to <math>FM</math> with respect <math>\angle BMC.</math>
+<i><b>Proof</b></i>
+<cmath>\angle BME = \angle BDE = \angle CDF = \angle CMF.</cmath>
+<cmath>\angle BMD = \angle BED = \angle AEC = \angle AMC. \blacksquare</cmath>
+'''vvsss'''
+==Isogonal of the bisector of the triangle==
+[[File:Bisector C.png|400px|right]]
+The triangle <math>ABC</math> be given. The point <math>D</math> chosen on the bisector <math>AA'.</math>
+Denote <cmath>B' = BD \cap AC, C' = CD \cap AB,</cmath>
+<cmath>E = BB' \cap A'C', F = CC' \cap A'B'.</cmath>
+Prove that <math>\angle BAE = \angle CAF.</math>
+<i><b>Proof</b></i>
+Let us perform a projective transformation of the plane that maps the point <math>A</math> to a point at infinity and the line <math>\ell = AA'</math> into itself.
+In this case, the images of segments <math>BC'</math> and <math>B'C</math> are equidistant from the image of <math>\ell \implies BC' || B'C || \ell.</math>
+Image of point <math>D</math> is midpoint of image <math>BB'</math> and midpoint image <math>CC' \implies</math>
+Image <math>BCB'C'</math> is parallelogramm <math>\implies</math>
+<math>BC = B'C' \implies \frac {DE}{BD} = \frac {DF}{CD} \implies </math> distances from <math>E</math> and <math>F</math> to <math>\ell</math> are equal <math>\implies</math>
+Preimages <math>AE</math> and <math>AF</math> are isogonals with respect <math>(\ell,A). \blacksquare</math>
+'''vladimir.shelomovskii@gmail.com, vvsss'''
+==Points on isogonals==
+[[File:Points on isogonals.png|400px|right]]
+The triangle <math>ABC</math> be given. The point <math>D</math> chosen on <math>BC.</math>
+The point <math>E</math> chosen on <math>BC</math> such that <math>AD</math> and <math>AE</math> are isogonals with respect <math>\angle BAC.</math>
+Prove that <math>\frac {AB^2}{BD \cdot BE} = \frac{ AC^2}{CD \cdot CE}.</math>
+<i><b>Proof</b></i>
+Denote <math>\angle BAD = \angle CAE = \varphi,</math>
+<math>\angle B = \beta, \angle C = \gamma \implies</math>
+<math>\angle ADE = \beta + \varphi, \angle AED = \gamma + \varphi, \angle BAE = \angle CAD = \psi+\varphi.</math>
+We use the Law of Sines and get:
+<cmath>\frac {AB}{BD} = \frac {\sin (\beta + \varphi)}{\sin \varphi}, \frac {AB}{BE} = \frac {\sin (\gamma + \varphi)}{\sin (\psi +\varphi)},</cmath>
+<cmath>\frac {AC}{CE} = \frac {\sin (\gamma + \varphi)}{\sin \varphi}, \frac {AC}{CD} = \frac {\sin (\beta + \varphi)}{\sin (\psi +\varphi)} \implies</cmath>
+<cmath>\frac {AB \cdot AB}{BD \cdot BE} = \frac {AC \cdot AC}{CD \cdot CE} =  \frac {\sin (\beta + \varphi) \cdot \sin (\gamma +\varphi)} {\sin \varphi \cdot \sin (\psi +\varphi)}.</cmath>
+'''vladimir.shelomovskii@gmail.com, vvsss'''
+==Trapezoid==
+[[File:Trapezoid3.png|370px|right]]
+The lateral side <math>CD</math> of the trapezoid <math>ABCD</math> is perpendicular to the bases, point <math>P</math> is the intersection point of the diagonals <math>ABCD</math>.
+Point <math>Q</math> is taken on the circumcircle <math>\omega</math> of triangle <math>PCD</math> diametrically opposite to point <math>P.</math>
+Prove that <math>\angle BQC = \angle AQD.</math>
+<i><b>Proof</b></i>
+WLOG, <math>CD</math> is not the diameter of <math>\omega.</math>
+Let sidelines <math>AD</math> and <math>BC</math> intersect <math>\omega</math> at points <math>D'</math> and <math>C',</math> respectively.
+<math>DD' \perp CD, CC' \perp CD \implies CDD'C'</math> is rectangle <math>\implies</math>
+<math>CC' = DD' \implies \angle CQC' = \angle DQD'.</math>
+<math>QE||BC</math> is isogonal to <math>QO</math> with respect <math>\angle CQD \implies</math>
+<math>QE||BC</math> is isogonal to <math>QP</math> with respect <math>\angle CQD \implies</math>
+In accordance with  <i><b>The isogonal theorem in case parallel lines</b></i> <math>\angle DQO = \angle CQE.</math>
+<math>QE||BC</math> is isogonal to <math>QP</math> with respect <math>\angle CQD, P = AC \cap BD \implies</math>
+<math>\angle AQD = \angle BQC</math> in accordance with <i><b>Converse theorem for The isogonal theorem in case parallel lines.</b></i> <math>\blacksquare</math>
+'''vladimir.shelomovskii@gmail.com, vvsss'''
 == Definition of isogonal conjugate of a point ==
-[[File:Definitin 1.png|400px|right]]
+[[File:Definitin 1.png|390px|right]]
-Let <math>P</math> be a point in the plane, and let <math>ABC</math> be a triangle.  We will denote by <math>a,b,c</math> the lines <math>BC, CA, AB</math>.  Let <math>p_a, p_b, p_c</math> denote the lines <math>PA</math>, <math>PB</math>, <math>PC</math>, respectively.  Let <math>q_a</math>, <math>q_b</math>, <math>q_c</math> be the reflections of <math>p_a</math>, <math>p_b</math>, <math>p_c</math> over the angle bisectors of angles <math>A</math>, <math>B</math>, <math>C</math>, respectively.  Then lines <math>q_a</math>, <math>q_b</math>, <math>q_c</math> [[concurrence | concur]] at a point <math>Q</math>, called the isogonal conjugate of <math>P</math> with respect to triangle <math>ABC</math>.
+Let triangle <math>\triangle ABC</math> be given. Let <math>\omega</math> be the circumcircle of <math>ABC.</math> Let point <math>P</math> be in the plane of <math>\triangle ABC, P \notin AB, P \notin BC, P \notin AC, P \notin \omega.</math>
+Denote by <math>a,b,c</math> the lines <math>BC, CA, AB,</math> respectively. Denote by <math>p_a, p_b, p_c</math> the lines <math>PA</math>, <math>PB</math>, <math>PC</math>, respectively.
+Denote by <math>q_a</math>, <math>q_b</math>, <math>q_c</math> the reflections of <math>p_a</math>, <math>p_b</math>, <math>p_c</math> over the angle bisectors of angles <math>A</math>, <math>B</math>, <math>C</math>, respectively.
+Prove that lines <math>q_a</math>, <math>q_b</math>, <math>q_c</math> [[concurrence | concur]] at a point <math>Q.</math>
+This point is called the isogonal conjugate of <math>P</math> with respect to triangle <math>ABC</math>.
 <i><b>Proof</b></i>
@@ Line 10: / Line 308: @@
 <cmath> \frac{\sin \angle q_a b}{\sin \angle c q_a} \cdot \frac{\sin \angle q_b c}{\sin \angle a q_b} \cdot \frac{\sin \angle q_c a}{\sin \angle b q_c} = \frac{\sin \angle p_a c}{\sin \angle b p_a} \cdot \frac{\sin \angle p_b a}{\sin \angle c p_b} \cdot \frac{\sin \angle p_c b}{\sin \angle a p_c} = 1, </cmath>
 so again by the trigonometric form of Ceva, the lines <math>q_a, q_b, q_c</math> concur, as was to be proven.  <math>\blacksquare</math>
+<i><b>Corollary</b></i>
+Let points P and Q lie on the isogonals with respect angles <math>\angle B</math> and <math>\angle C</math> of triangle <math>\triangle ABC.</math>
+Then these points lie on isogonals with respect angle <math>\angle A.</math>
+<i><b>Corollary 2</b></i>
+Let point <math>P</math> be in the sideline <math>BC</math> of <math>\triangle ABC, P \ne B, P \ne C.</math>
+Then the isogonal conjugate of a point <math>P</math> is a point <math>A.</math>
+Points <math>A,B,</math> and <math>C</math> do not have an isogonally conjugate point.
+'''vladimir.shelomovskii@gmail.com, vvsss'''
+==Three points==
+[[File:3 points.png|400px|right]]
+Let fixed triangle <math>ABC</math> be given. Let the arbitrary point <math>D</math> not be on sidelines of <math>\triangle ABC.</math> Let <math>E</math> be the point on isogonal of <math>CD</math> with respect angle <math>\angle ACB.</math>
+Let <math>F</math> be the crosspoint of isogonal of <math>BD</math> with respect angle <math>\angle ABC</math> and isogonal of <math>AE</math> with respect angle <math>\angle BAC.</math>
+Prove that lines <math>AD, BE,</math> and <math>CF</math> are concurrent.
+<i><b>Proof</b></i>
+Denote <math>D' = BF \cap CE, S = CF \cap BE.</math>
+<math>AE</math> and <math>AF</math> are isogonals with respect <math>\angle BAC \implies</math>
+<math>D'</math> and S lie on isogonals of <math>\angle BAC.</math>
+<math>\angle DBC = \angle D'BA, \angle DCB = \angle D'CA \implies</math>
+<math>D'</math> is isogonal conjugated of <math>D</math> with respect <math>\triangle ABC \implies</math>
+<math>D'</math> and <math>D</math> lie on isogonals of <math>\angle BAC.</math>
+Therefore points <math>A, S</math> and <math>D</math> lie on the same line which is isogonal to <math>AD'</math>  with respect <math>\angle BAC. \blacksquare</math>
+'''vladimir.shelomovskii@gmail.com, vvsss'''
 == Second definition ==
-[[File:Definition 2.png|400px|right]]
+[[File:Definition 2.png|370px|right]]
 Let triangle <math>\triangle ABC</math> be given. Let point <math>P</math> lies in the plane of <math>\triangle ABC,</math>
 <cmath>P \notin AB, P \notin BC, P \notin AC.</cmath>
@@ Line 19: / Line 358: @@
 Then the circumcenter <math>Q</math> of the <math>\triangle P_1P_2P_3</math> is the isogonal conjugate of <math>P.</math>
+Points <math>A, B,</math> and <math>C</math> have not isogonal conjugate points.
+Another points of sidelines <math>BC, AC, AB</math> have points <math>A, B, C,</math> respectively as isogonal conjugate points.
 <i><b>Proof</b></i>
 <cmath>PC = P_1C, PC = P_2C \implies P_1C = P_2C.</cmath>
 <cmath>\angle ACQ = \angle BCP_1 \implies \angle QCP_1 = \angle ACB.</cmath>
 <cmath>\angle BCQ = \angle ACP_2 \implies \angle QCP_2 = \angle ACB.</cmath>
-<math>\angle QCP_1 = \angle QCP_2, CP_1 = CP_2, QC</math> common <math>\implies</math>
+<math>\angle QCP_1 = \angle QCP_2, CP_1 = CP_2, QC</math> is common therefore
 <cmath>\triangle QCP_1 = \triangle QCP_2 \implies QP_1 = QP_2.</cmath>
 Similarly  <math>QP_1 = QP_3 \implies Q</math> is  the circumcenter of the <math>\triangle P_1P_2P_3.</math> <math>\blacksquare</math>
+From definition 1 we get that <math>P</math> is the isogonal conjugate of <math>Q.</math>
+It is clear that each point <math>P</math> has the unique isogonal conjugate point.
 Let point <math>P</math> be the point with barycentric coordinates <math>(p : q : r),</math>
-<cmath>p = [(P-B),(P-C)], q = [(P-C),(P-A)], r = [(P-A),(P-B)].</cmath>
+<cmath>p = [(P - B),(P - C)], q = [(P - C),(P - A)], r = [(P - A),(P - B)].</cmath>
 Then <math>Q</math> has barycentric coordinates <cmath>(p' : q' : r'), p' = \frac {|B - C|^2}{p}, q' = \frac {|A-C|^2}{q}, r' = \frac {|A - B|^2}{r}.</cmath>
 '''vladimir.shelomovskii@gmail.com, vvsss'''
 ==Distance to the sides of the triangle==
 [[File:Distances to.png|450px|right]]
@@ Line 45: / Line 393: @@
 Let <math>\theta = \angle ACP = \angle BCQ, \Theta =  \angle ACQ = \angle BCP.</math>
-<math>\frac {PE}{PD} = \frac {PC \sin \theta}{PC \sin \Theta} = \frac {QC \sin \theta}{QC \sin \Theta}  = \frac {QD'}{QE'}.</math>
+<cmath>\frac {PE}{PD} = \frac {PC \sin \theta}{PC \sin \Theta} = \frac {QC \sin \theta}{QC \sin \Theta}  = \frac {QD'}{QE'}. \blacksquare</cmath>
 '''vladimir.shelomovskii@gmail.com, vvsss'''
+==Sign of isogonally conjugate points==
+[[File:Isog dist.png|350px|right]]
+[[File:Isog distance.png|350px|right]]
+Let triangle <math>\triangle ABC</math> and points <math>P</math> and <math>Q</math> inside it be given.
+Let <math>D, E, F</math> be the projections <math>P</math> on sides <math>BC, AC, AB,</math> respectively.
+Let <math>D', E', F'</math> be the projections <math>Q</math> on sides <math>BC, AC, AB,</math> respectively.
+Let <math>\frac {PE}{PD} = \frac{QD'}{QE'}, \frac {PF}{PD} = \frac{QD'}{QF'}.</math> Prove that point <math>Q</math> is the isogonal conjugate of a point <math>P</math> with respect to a triangle <math>\triangle ABC.</math>
+One can prove a similar theorem in the case <math>P</math> outside <math>\triangle ABC.</math>
+<i><b>Proof</b></i>
+<cmath>\frac {PE}{PD} = \frac {PE}{PC} : \frac {PD}{PC} = \frac {\sin \angle ACP}{\sin \angle BCP},</cmath>
+<cmath>\frac {QD'}{QE'} = \frac {QD'}{QC} : \frac {QE'}{QC} = \frac {\sin \angle BCQ}{\sin \angle ACQ}.</cmath>
+Denote <math>\angle ACP = \varphi, \angle BCQ = \psi, \angle ACB = \gamma.</math>
+<cmath>\sin \varphi \cdot \sin (\gamma - \psi) = \sin \psi \cdot \sin (\gamma - \varphi) \implies</cmath>
+<cmath>\cos (\varphi - \gamma + \psi) - \cos(\varphi + \gamma - \psi) =  \cos (\psi - \gamma + \varphi) - \cos(\psi + \gamma - \varphi)</cmath>
+<cmath>\cos (\gamma + \varphi - \psi) = \cos(\gamma - \psi + \varphi) \implies</cmath>
+<cmath>\cos \gamma \cos (\varphi - \psi) - \sin \gamma \sin (\varphi - \psi) =  \cos \gamma \cos (\varphi - \psi) + \sin \gamma \sin (\varphi - \psi)</cmath>
+<cmath>2 \sin \gamma \cdot \sin (\varphi - \psi) = 0, \varphi + \psi < 180^\circ \implies \varphi = \psi.</cmath>
+Similarly <math>\angle ABP = \angle CBQ.</math>
+Hence point <math>Q</math> is the isogonal conjugate of a point <math>P</math> with respect to a triangle <math>\triangle ABC. \blacksquare</math>
+'''vladimir.shelomovskii@gmail.com, vvsss'''
 ==Circumcircle of pedal triangles==
-[[File:Common circle.png|380px|right]]
+[[File:Common circle.png|330px|right]]
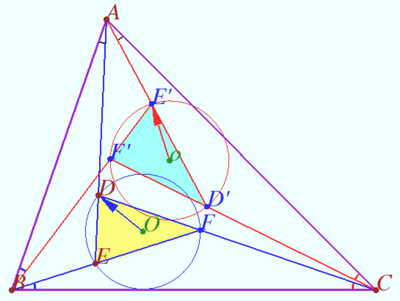
 Let <math>Q</math> be the isogonal conjugate of a point <math>P</math> with respect to a triangle <math>\triangle ABC.</math>
 Let <math>E, D, F</math> be the projection <math>P</math> on sides <math>AC, BC, AB,</math> respectively.
 Let <math>E', D', F'</math> be the projection <math>Q</math> on sides <math>AC, BC, AB,</math> respectively.
-Then points <math>D, D', E, E', F, F'</math> are concyclic. The midpoint <math>PQ</math> is circumcenter of <math>DD'EE'FF'.</math>
+Prove that points <math>D, D', E, E', F, F'</math> are concyclic.
+The midpoint <math>PQ</math> is circumcenter of <math>DD'EE'FF'.</math>
 <i><b>Proof</b></i>
 Let <math>\theta = \angle ACP = \angle BCQ, \Theta =  \angle ACQ = \angle BCP.</math>
 <math>CE \cdot CE' = PC \cos \theta \cdot QC \cos \Theta = PC \cos \Theta \cdot QC \cos \theta = CD \cdot CD'.</math>
 Hence points <math>D, D', E, E'</math> are concyclic.
-The midpoint <math>PQ</math> is circumcenter of <math>DD'EE'FF'.</math>
+<math>PQE'E</math> is trapezoid, <math>E'E \perp PE \implies OE = OE' \implies</math>
+the midpoint <math>PQ</math> is circumcenter of <math>DD'EE'.</math>
 Similarly points <math>D, D', F, F'</math> are concyclic and points <math>F, F', E, E'</math> are concyclic.
-Therefore points <math>D, D', E, E', F, F'</math> are concyclic.
+Therefore points <math>D, D', E, E', F, F'</math> are concyclic, so the midpoint <math>PQ</math> is circumcenter of <math>DD'EE'FF'.</math>
-The midpoint <math>PQ</math> is circumcenter of <math>DD'EE'FF'.</math>
+'''vladimir.shelomovskii@gmail.com, vvsss'''
+==Common circumcircle of the pedal triangles as the sign of isogonally conjugate points==
+Let triangle <math>\triangle ABC</math> and points <math>P</math> and <math>Q</math> inside it be given. Let <math>D, E, F</math> be the projections <math>P</math> on sides <math>BC, AC, AB,</math> respectively.
+Let <math>D', E', F'</math> be the projections <math>Q</math> on sides <math>BC, AC, AB,</math> respectively.
+Let points <math>D, E, F, D', E', F'</math> be concyclic and none of them lies on the sidelines of <math>\triangle ABC.</math>
+Then point <math>Q</math> is the isogonal conjugate of a point <math>P</math> with respect to a triangle <math>\triangle ABC.</math>
+This follows from the uniqueness of the conjugate point and the fact that the line intersects the circle in at most two points.
+'''vladimir.shelomovskii@gmail.com, vvsss'''
+==Two pares of isogonally conjugate points==
+[[File:3 pare of points.png|400px|right]]
+Let triangle <math>\triangle ABC</math> and points <math>X</math> and <math>Y</math> be given. Let points <math>X'</math> and <math>Y'</math> be the isogonal conjugate of a points <math>X</math> and <math>Y</math> with respect to a triangle <math>\triangle ABC,</math> respectively.
+Let <math>XY</math> cross <math>X'Y'</math> at <math>Z</math> and <math>XY'</math> cross <math>X'Y</math> at <math>Z'.</math>
+Prove that point <math>Z'</math> is the isogonal conjugate of a point <math>Z</math> with respect to <math>\triangle ABC.</math>
+<i><b>Proof</b></i>
+There are two pairs of isogonals <math>CX - CX'</math> and <math>CY - CY'</math> with respect to the angle <math>\angle ACB \implies</math>
+<math>CZ - CZ'</math> are isogonals with respect to the <math>\angle ACB</math> in accordance with <i><b>The isogonal theorem</b></i>.
+Similarly <math>AZ - AZ'</math> are the isogonals with respect to the <math>\angle BAC.</math>
+Therefore the point <math>Z'</math> is the isogonal conjugate of a point <math>Z</math> with respect to <math>\triangle ABC.</math>
+'''vladimir.shelomovskii@gmail.com, vvsss'''
+==Circles==
+[[File:2 points isogon.png|300px|right]]
+Let <math>Q</math> be the isogonal conjugate of a point <math>P</math> with respect to a triangle <math>\triangle ABC.</math>
+Let <math>D</math> be the circumcenter of <math>\triangle BCP.</math>
+Let <math>E</math> be the circumcenter of <math>\triangle BCQ.</math>
+Prove that points <math>D</math> and <math>E</math> are inverses with respect to the circumcircle of <math>\triangle ABC.</math>
+<i><b>Proof</b></i>
+The circumcenter of <math>\triangle ABC</math> point <math>O,</math> and points <math>D</math> and <math>E</math> lies on  the perpendicular bisector of <math>BC.</math>
+<cmath>\angle BOD = \angle COE = \angle BAC.</cmath>
+<cmath>2 \angle BDO = \angle BDC = \overset{\Large\frown} {BC} =</cmath>
+<cmath>= 360^\circ - \overset{\Large\frown} {CB} = 360^\circ - 2 \angle BPC.</cmath>
+<cmath>\angle BDO = 180^\circ - \angle BPC = \angle PBC + \angle PCB.</cmath>
+Similarly <math>\angle CEO = 180^\circ - \angle BQC = \angle QBC + \angle QCB.</math>
+<cmath>\angle PBC + \angle QBC = \angle PBC + \angle PBA = \angle ABC.</cmath>
+<cmath>\angle QCB + \angle PCB = \angle QCB + \angle QCA = \angle ACB.</cmath>
+<cmath>\angle CEO +\angle BDO = \angle ABC + \angle ACB = 180^\circ - \angle BAC \implies</cmath>
+<cmath>\angle OBD = 180^\circ - \angle BOD - \angle BDO = \angle OEC \implies</cmath>
+<cmath>\triangle OBD \sim \triangle OEC \implies \frac {OB}{OE} = \frac {OD}{OC} \implies OD \cdot OE = OB^2. \blacksquare</cmath>
+'''vladimir.shelomovskii@gmail.com, vvsss'''
+==Equidistant isogonal conjugate points==
+[[File:Equal distances.png|330px|right]]
+[[File:Equidistant points.png|330px|right]]
+Let triangle <math>ABC</math> with incenter <math>I</math> be given.
+Denote <math>\omega = \odot BIC.</math>
+Let point <math>P'</math> be the isogonal conjugate of the point <math>P</math> with respect to <math>\triangle ABC.</math>
+Prove that <math>AP = AP'</math> iff <math>P \in \omega.</math>
+<i><b>Proof</b></i>
+. Let <math>P \in \omega.</math> WLOG, <math>P \in \angle BAI.</math>
+Point <math>P \in \omega \implies \angle PBI = \angle PCI.</math>
+Point <math>P'</math> is the isogonal conjugate of the point <math>P</math> with respect to <math>\triangle ABC \implies</math>
+<cmath>\angle PBI = \angle P'BI, \angle PCI = \angle P'CI \implies \angle P'BI = \angle P'CI.</cmath>
+So points <math>B,C,I, P,</math> and <math>P'</math> are concyclic.
+Let <math>E = AI \cap \odot ABC.</math> Then <math>E</math> is the center of <math>\omega \implies</math>
+<cmath>EP = EP', \angle IEP = \angle IEP' = 2 \angle PBI.</cmath>
+<cmath>\triangle AEP = \triangle AEP' \implies AP = AP'.</cmath>
+. Let <math>AP = AP'.</math>
+<math>\angle PAI = \angle PAE = \angle P'AI = \angle P'AE \implies</math>
+Points <math>P</math> and <math>P'</math> are symmetric with respect <math>AI \implies PE = P'E.</math>
+Suppose that <math>P \notin \odot BIC.</math>
+Let <math>O</math> be the center of <math>\odot BPC, O'</math> be the center of <math>\odot BP'C.</math>
+It is known that points <math>O</math> and <math>O'</math> are inverted with respect to the circumcircle of <math>\triangle ABC.</math>
+Points <math>O, O',</math> and <math>E</math> belong to bisector <math>BC, E \in \odot ABC.</math>
+Therefore <math>\overset{\Large\frown} {BIC}</math> divide <math>\overset{\Large\frown} {BPC}</math> and <math>\overset{\Large\frown} {BP'C}.</math>
+WLOG (see diagram) <math>PE > IE > P'E,</math> contradiction.
+'''vladimir.shelomovskii@gmail.com, vvsss'''
+==Simplified distance formula for isogonal points==
+[[File:1 pare and.png|370px|right]]
+Let triangle <math>\triangle ABC,</math> points <math>P</math> and <math>P',</math> and <math>\odot ABC = \Omega</math> be given. Let point <math>P'</math> be the isogonal conjugate of a point <math>P</math> with respect to a triangle <math>\triangle ABC.</math>
+<cmath>D = AP \cap BC, E = AP' \cap BC, F = AP \cap \Omega, G = AP' \cap \Omega.</cmath>
+Prove that <math>PF \cdot P'G= AF \cdot EG.</math>
+<i><b>Proof</b></i>
+<math>\angle AFC</math> and <math>\angle AGC</math> are both subtended by arc <math>\overset{\Large\frown} {AC} \implies \angle AFC = \angle AGC.</math>
+<cmath>\angle PCF = \angle PCB + \angle BCF = \angle P'CA + \angle BAF = \angle P'CA + \angle P'AC=</cmath>
+<cmath>= \angle GP'C \implies \triangle CPF \sim \triangle P'CG \implies PF \cdot P'G = FC \cdot CG.</cmath>
+Similarly <cmath>\triangle CAF \sim \triangle ECG \implies AF \cdot EG = FC \cdot CG.</cmath>
+[[Barycentric coordinates | Product of isogonal segments]]
+'''vladimir.shelomovskii@gmail.com, vvsss'''
+==Point on circumcircle==
+[[File:RADAX.png|350px|right]]
+Let triangle <math>\triangle ABC,</math> points <math>D \in BC</math> and <math>E \in BC</math> be given.
+Denote <math>\Omega = \odot ABC, \omega = \odot AED, G = \omega \cap \Omega \ne A, F = AG \cap BC,</math>
+<cmath>K = AE \cap \Omega \ne A, L = GD \cap \Omega \ne G.</cmath>
+Prove that <math>KL || BC.</math>
+<i><b>Proof</b></i>
+WLOG, the order of the points is <math>B,E,F,C,D,</math> as shown on diagram.
+The spiral symilarity centered at <math>A</math> maps <math>\Omega</math> to <math>\omega</math> and point <math>L \in \Omega</math> to point <math>D \in \omega \implies \overset{\Large\frown} {AL} = \overset{\Large\frown} {AD} \implies \angle ABL = \angle AED.</math>
+<math>\angle AED</math> is the external angle of <math>\triangle AEB \implies \angle AED = \angle ABC + \angle BAE \implies</math>
+<cmath>\angle CBL = \angle BAK \implies \overset{\Large\frown} {BK} = \overset{\Large\frown} {CL} \implies BC ||KL. \blacksquare</cmath>
+<i><b>Corollary</b></i>
+<math>AL</math> is the isogonal conjugate to <math>AK</math> with respect <math>\angle BAC.</math>
+'''vladimir.shelomovskii@gmail.com, vvsss'''
+==Fixed point on circumcircle==
+[[File:Fixed point 2.png|280px|right]]
+[[File:Fixed point 3.png|280px|right]]
+[[File:Fixed point 4.png|280px|right]]
+[[File:Fixed point 5.png|280px|right]]
+Let triangle <math>\triangle ABC,</math> point <math>G \ne A</math> on circumcircle <math>\Omega = \odot ABC,</math> and point <math>D \in BC</math> be given.
+Point <math>P</math> lies on <math>AG,</math> point <math>P'</math> be the isogonal conjugate of a point <math>P</math> with respect to a triangle <math>\triangle ABC, Q = DP' \cap AP, F = \odot DPQ \cap \Omega.</math>
+Prove that <math>F</math> is fixed point and not depends from position of <math>P.</math>
+<i><b>Proof</b></i>
+WLOG, the order of points on sideline is <math>B, C, D,</math> point <math>B</math> is closer to <math>AP</math> than to <math>AP'.</math>
+Denote <math>Y = AP \cap BC, Z = AP' \cap BC,\omega = \odot ADY,</math>
+<cmath>F' = \omega \cap \Omega \ne A,  H = \Omega \cap F'D \ne F'.</cmath>
+Spiral similarity centered at <math>A</math> which maps <math>\Omega</math> into <math>\odot AYD</math> transform point <math>H</math> into point <math>D \implies</math>
+<cmath>\overset{\Large\frown} {ACH} =  \overset{\Large\frown} {AD} \implies \angle AGH = \angle AYD \implies GH||BC \implies</cmath>  <cmath>\overset{\Large\frown} {CH} =  \overset{\Large\frown} {BG} \implies \angle BAG = \angle CAH \implies H \in AP'.</cmath>
+Points <math>F', H,</math> and <math>D</math> are collinear.
+It is known ([[Barycentric coordinates | Ratio of isogonal segments]]) that  <math>\frac {AP'}{P'Z} \cdot \frac {AP}{PY} = \frac {AH}{HZ}.</math>
+We use the ratio of the areas and get:
+<cmath>\frac {[AQD]}{[QYD]} = \frac{AQ}{QY}, \frac {[ZQD]}{[YQD]} = \frac{ZD}{YD},</cmath>
+<cmath>\frac {[AQD]}{[ZQD]} = \frac{AP'}{P'Z} \implies</cmath>
+<cmath> \frac{AQ}{QY} = \frac {[AQD]}{[QYD]} = \frac {[AQD]}{[ZQD]} \cdot \frac {[ZQD]}{[YQD]} = \frac{AP'}{P'Z} \cdot \frac{ZD}{YD}.</cmath>
+Denote <math>X = AP \cap DH.</math>
+<cmath>\frac {[AXD]}{[YXD]} = \frac{AX}{XY}, \frac {[XZD]}{[XYD]} = \frac{ZD}{YD},</cmath>
+<cmath>\frac {[AXD]}{[XZD]} = \frac{AH}{HZ} \implies</cmath>
+<cmath> \frac{AX}{XY} = \frac {[AXD]}{[YXD]} = \frac {[AXD]}{[XZD]} \cdot \frac {[XZD]}{[YXD]} = \frac{AH}{HZ} \cdot \frac{ZD}{YD}.</cmath>
+Therefore <math>\frac{AX}{XY} =  \frac{AQ}{QY} \cdot \frac{AP}{PY}</math> which means ([[Radical axis | Problems | Simple]]) that <math>DX</math> is the radical axes of <math>\omega</math> and <math>\odot DPQ \implies</math>
+<math>F = F'</math> and not depends from position of <math>P.</math>
+[[Barycentric coordinates | Fixed point on circumcircle]]
+'''vladimir.shelomovskii@gmail.com, vvsss'''
+==Distance formula for isogonal points==
+[[File:Isogonal formulas.png|400px|right]]
+Let triangle <math>\triangle ABC</math> and point <math>P</math> be given.
+Let point <math>P'</math> be the isogonal conjugate of a point <math>P</math>  with respect to a triangle <math>\triangle ABC.</math>
+Let lines <math>AP</math> and <math>AP'</math> cross sideline <math>BC</math> at <math>D</math>  and <math>E</math> and circumcircle of <math>\triangle ABC</math> at <math>F</math> and <math>G,</math> respectively.
+We apply the Isogonal’s property and get <math>\frac {BD}{DC} \cdot \frac{BE}{EC} = \frac {AB^2}{AC^2}.</math>
+<math>EF || BC.</math> We apply the Ptolemy's theorem to <math>BCGF</math> and get <cmath>BC \cdot FG = BG^2 – BF^2.</cmath>
+We apply the barycentric coordinates and get
+<cmath>\left| \frac{BE}{EC} - \frac {BD}{DC} \right| = \frac {AB \cdot BC \cdot FG}{AC \cdot PF \cdot P'G}.</cmath>
+*[[Barycentric coordinates]]
 '''vladimir.shelomovskii@gmail.com, vvsss'''
+==Miquel point for isogonal conjugate points==
+[[File:Miquel of one pare.png|370px|right]]
+[[File:Miquel 1 pare.png|370px|right]]
+Let triangle <math>\triangle ABC,</math> points <math>Q \in BC</math> and <math>P</math> be given. Let point <math>P'</math> be the isogonal conjugate of a point <math>P</math> with respect to a triangle <math>\triangle ABC.</math>
+<cmath>D = QP \cap AP', E = AP \cap QP'.</cmath>
+Let <math>M</math> be the Miquel point of a complete quadrilateral <math>PDP'E.</math>
+Prove that <math>M</math> lies on the circumcircle of <math>\triangle ABC.</math>
+<i><b>Proof</b></i>
+Point <math>A</math> is the isogonal conjugate of a point <math>Q</math> with respect to a triangle <math>\triangle ABC,</math> so point <math>D</math> is the isogonal conjugate of a point <math>E</math> with respect to a triangle <math>\triangle ABC.</math>
+Points <math>P</math> and <math>E</math> lies on the same line, therefore <cmath>PF \cdot P'G = EF \cdot DG \implies</cmath>
+<cmath>\frac {PF-EP}{PF} = \frac{DG-DP'}{DG} \implies \frac {EP}{PF} = \frac{DP'}{DG}.</cmath>
+Point <math>M</math> lies on circles <math>APD</math> and <math>AEP' \implies </math> spiral similarity centered at <math>M</math> transform triangle <math>\triangle MPE</math> to <math>\triangle MDP' \implies</math>
+<cmath>\angle MPE = \angle MDP', \frac {MP}{MD} = \frac {PE}{DP'} = \frac{PF}{DG} \implies</cmath>
+<cmath>\triangle MPF \sim \triangle MDG \implies</cmath> <cmath>\angle AFM = \angle AGM \implies M \in \odot ABC.</cmath>
+'''vladimir.shelomovskii@gmail.com, vvsss'''
+==Point on circumcircle==
+[[File:Point on circumcircle 0.png|400px|right]]
+Let triangle <math>\triangle ABC,</math> and points <math>D \in BC</math> and <math>E \in \odot ABC = \Omega</math> be given.
+Let <math>\odot ADE = \omega, F = BC \cap \omega \ne D.</math>
+Let lines <math>AF</math> and <math>AG (G \in BC)</math> be the isogonals with respect to the angle <math>\angle BAC, \odot AGD = \theta.</math>
+Let <math>P</math> be an arbitrary point on <math>AF, Q = DP \cap AG, H = \theta \cap \Omega.</math>
+Prove that <math>X = EP \cap HQ</math> lies on <math>\Omega.</math>
+===Simplified problem===
+Let <math>\triangle ABC,</math> and points <math>D \in BC</math> and <math>E \in \odot ABC = \Omega</math> be given, <math>\omega = \odot ADE, F = \omega \cap BC \ne D.</math>
+Let lines <math>AF</math> and <math>AG (G \in BC)</math> be the isogonals with respect to <math>\angle BAC, \theta = \odot AGD, H = \theta \cap \Omega.</math>
+Prove that <math>X = EF \cap HG \in \Omega.</math>
+[[File:Point on circumcircle 1.png|400px|right]]
+<i><b>Proof, Simplified problem</b></i>
+<cmath>\angle CGH = \angle DAH = \frac{1}{2} \overset{\Large\frown} {HD} (\theta),</cmath>
+<cmath>\angle DFE = \angle DAE = \frac{1}{2} \overset{\Large\frown} {ED} (\omega),</cmath>
+<cmath>\angle EAH = \angle DAE - \angle DAH = \frac{1}{2} \overset{\Large\frown} {EH}(\Omega),</cmath>
+<cmath>\angle EXH = \angle DFE - \angle DGH = \angle EAH \implies</cmath>
+points <math>A, H, E, X</math> are concyclic on <math>\Omega.</math>
+<i><b>Proof</b></i>
+[[File:Point on circumcircle 2.png|400px|right]]
+Let points <math>P'</math> and <math>Q'</math> be the isogonal conjugate of a points <math>P</math> and <math>Q</math> with respect to a triangle <math>\triangle ABC, \omega' = \odot Q'PD, \theta' = \odot P'QD.</math>
+It is known that <math>E \in \omega', H \in \theta', \omega' \cap \theta' \cap \Omega = M.</math>
+<cmath>\angle DQH = \angle DMH = \frac{1}{2} \overset{\Large\frown} {HD} (\theta'),</cmath>
+<cmath>\angle DPE = \angle DME = \frac{1}{2} \overset{\Large\frown} {ED} (\omega'),</cmath>
+<cmath>\angle EMH = \angle DME - \angle DMH = \frac{1}{2} \overset{\Large\frown} {EH}(\Omega),</cmath>
+<cmath>\angle EXH = \angle DPE - \angle DQH = \angle EMH \implies</cmath>
+points <math>M, H, E, X</math> are concyclic on <math>\Omega.</math>
+'''vladimir.shelomovskii@gmail.com, vvsss'''
+==Isogonal of line BC with respect to angle BAC==
+[[File:Isogonal of BC.png|350px|right]]
+Let triangle <math>\triangle ABC</math> be given, <math>\Omega = \odot ABC, AD || BC.</math>
+Let lines <math>AE</math> and <math>AD</math> be the isogonals with respect to <math>\angle BAC.</math>
+Prove that <math>AE</math> is tangent to <math>\Omega.</math>
+<i><b>Proof</b></i>
+Let <math>O</math> and <math>H</math> be the circumcenter and the orthocenter of <math>\triangle ABC,</math> respectively.
+<cmath>AH \perp BC, AD || BC \implies AH \perp AD.</cmath>
+<math>AH</math> is isogonal to <math>AO</math> with respect to <math>\angle BAC \implies AE \perp AO \implies AE</math> is tangent to <math>\Omega.</math>
+'''vladimir.shelomovskii@gmail.com, vvsss'''
+==Isogonal bijection lines and points==
+[[File:Isogonal of l.png|350px|right]]
+Let triangle <math>\triangle ABC</math> and line <math>\ell, P \in \ell</math> be given, <math>\Omega = \odot ABC.</math>
+Define <math>G \in \Omega</math> the point with property  <math>G' \in \ell.</math>
+Prove that <math>\angle ABG</math> is equal the angle <math>\theta</math> between <math>\ell</math> and <math>BC.</math>
+<i><b>Proof</b></i>
+WLOG, the configuration is the same as shown on diagram, <math>F = \ell \cap BC, AD' || \ell,  \theta = \angle PFB, AD || BC, AE</math> is the tangent to <math>\Omega.</math>
+<math>AD</math> is isogonal to <math>AE, AD'</math> is isogonal to <math>AG</math> with respect to <math>\angle BAC \implies</math>
+<cmath>\theta = \angle PFB = \angle D'AD = \angle GAE = \angle GBA.</cmath>
+A bijection has been established between the set of lines parallel to a given one and the set of points of the circumcircle.
+'''vladimir.shelomovskii@gmail.com, vvsss'''
+==Miquel point for two pare isogonal points==
+[[File:2 pare Miquel o.png|400px|right]]
+Let triangle <math>\triangle ABC</math> and points <math>P</math> and <math>Q</math> be given.
+Let points <math>P'</math> and <math>Q'</math> be the isogonal conjugate of the points <math>P</math> and <math>Q</math> with respect to <math>\triangle ABC, \Omega = \odot ABC, M</math> is the Miquel point of quadrilateral <math>PQP'Q'.</math>
+Prove that <math>M \in \Omega.</math>
+<i><b>Proof</b></i>
+Denote <math>R = PQ \cap P'Q', \Theta = \odot P'QR, \theta = \odot PQ'R.</math>
+Then <math>M = \theta \cap \Theta</math> is the Miquel point of quadrilateral <math>PQP'Q'.</math>
+Denote <math>E = \theta \cap \Omega \notin \Theta, F = \Theta \cap \Omega \notin \theta.</math>
+Let <math>D \in \Omega</math> be the point with property <math>D' \in PQ.</math>
+WLOG, configuration is similar as shown in diagram.
+<math>P' \in DF, Q' \in DE</math> ([[Isogonal_conjugate | Isogonal_bijection_lines_and_points]]).
+<cmath>\angle EMF = \angle RME - \angle RMF = \angle RQ'E - \angle RP'F = \angle P'Q'E - \angle DP'Q' = \angle P'DQ' = \angle EDF \implies M \in \odot DEF  \blacksquare</cmath>
+'''vladimir.shelomovskii@gmail.com, vvsss'''
+==Isogonic center’s conjugate point==
+[[File:Fermat 1.png|500px|right]]
+[[File:Fermat 2.png|300px|right]]
+Let triangle <math>ABC</math> with isogonic center <math>F (X(13)</math> or <math>X(14))</math> be given. Denote <math>\omega = \odot BIC.</math>
+Let line <math>\ell_A</math> be the axial symmetry of line <math>AF</math> according to the sideline <math>BC.</math>
+Define lines <math>\ell_B</math> and <math>\ell_C</math> similarly.
+Prove that the lines <math>\ell_A, \ell_B,</math> and <math>\ell_C</math> are concurrent.
+<i><b>Proof</b></i>
+Let <math>I</math> be the incenter of <math>\triangle ABC, F =X(13).</math>
+<cmath>A_1 = AF \cup BC, E = AI \cup BC, D \in BC, AD \perp AE, \omega = \odot AED.</cmath>
+Let <math>F_1 = AF \cup \omega, F'</math> is simmetric to <math>F_1</math> with respect <math>BC \implies A_1F' = \ell_A.</math>
+The diameter <math>DE</math> of <math>\omega</math> lies on <math>BC \implies F_1 \in \omega, \overset{\Large\frown} {EF_1} = \overset{\Large\frown} {EF'} \implies \angle EAF_1 = \angle EAF'.</math>
+Therefore <math>AF'</math> is the isogonal conjugate of <math>AF</math> with respect to <math>\angle BAC.</math>
+Similarly <math>\ell_B</math> and <math>\ell_C</math> are the isogonal conjugate of <math>BF</math> and <math>CF,</math> so point <math>F'</math> is the isogonal conjugate of point <math>F</math> with respect to <math>\triangle ABC.</math>
+The second diagram show construction in the case <math>F =X(14).</math> The proof is similar.
+'''vladimir.shelomovskii@gmail.com, vvsss'''
+==Three pairs isogonal points==
+[[File:Shar 2024 20.png|400px|right]]
+Let a triangle <math>ABC,</math> points <math>D</math> and <math>E \in AD</math> be given, <math>F = CD \cap BE.</math>
+Points <math>D', E'</math> and <math>F'</math> are the isogonal conjugate of the points <math>D, E,</math> and <math>F,</math> respectively, with respect to <math>\triangle ABC.</math>
+Prove that <math>\frac {AD}{AE} \cdot \frac {BE}{BF} \cdot \frac {CF}{CD} = \frac {AE'}{AD'} \cdot \frac {BF'}{BE'} \cdot \frac {CD'}{CF'}.</math>
+<i><b>Proof</b></i>
+Denote <math>\angle BAC = \alpha, \angle ABC = \beta, \angle ACB = \gamma,</math>
+<cmath>\angle BAD = \varphi_A, \angle CBE = \varphi_B, \angle ACD = \varphi_C.</cmath>
+We use isogonal properties and get
+<cmath>\angle CAD' = \varphi_A, \angle ABE' = \varphi_B, \angle BCD' = \varphi_C.</cmath>
+By applying the Law of Sines, we get <cmath>\frac {BE}{AE} = \frac {\sin \varphi_A}{\sin (\beta - \varphi_B)}, \frac {CF}{BF} = \frac {\sin \varphi_B}{\sin (\gamma - \varphi_C)}, \frac {AD}{CD} = \frac {\sin \varphi_C}{\sin (\alpha - \varphi_A)}.</cmath>
+Symilarly, <cmath>\frac {AE'}{BE'} = \frac {\sin \varphi_B}{\sin (\alpha - \varphi_A)}, \frac {BF'}{CF'} = \frac {\sin \varphi_C}{\sin (\beta - \varphi_B)}, \frac {CD'}{AD'} = \frac {\sin \varphi_A}{\sin (\gamma - \varphi_C)}.</cmath>
+We multiply these equations and get
+<cmath>\frac {AE \cdot BF \cdot CD}{AD \cdot BE \cdot CF} = \frac{AD' \cdot BE' \cdot CF'}{AE' \cdot BF' \cdot CD'} = \frac {\sin \varphi_A \cdot \sin \varphi_B \cdot \sin \varphi_C}{\sin (\alpha - \varphi_A) \cdot \sin (\beta - \varphi_B) \cdot \sin (\gamma - \varphi_C)}.</cmath>
+'''vladimir.shelomovskii@gmail.com, vvsss'''
+==Ratio for three pairs of isogonal points==
+[[File:Shar 2024 20 1.png|400px|right]]
+[[File:Shar 2024 20 2.png|400px|right]]
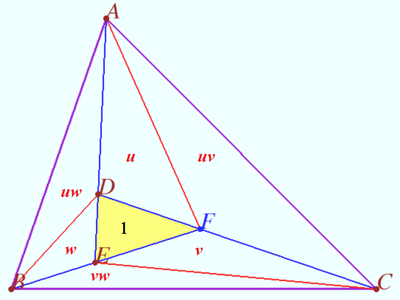
+Let a triangle <math>ABC,</math> points <math>D</math> and <math>E \in AD</math> be given, <math>F = CD \cap BE.</math>
+Points <math>D', E'</math> and <math>F'</math> are the isogonal conjugate of the points <math>D, E,</math> and <math>F,</math> respectively, with respect to <math>\triangle ABC.</math>
+Denote <math>R</math> and <math>R'</math> the circumradii of triangles <math>\triangle DEF</math> and <math>\triangle D'E'F',</math> respectively.
+Prove that <math>\frac {AD \cdot BE \cdot CF}{R} = \frac {AE' \cdot BF' \cdot CD'}{R'}.</math>
+<i><b>Proof</b></i>
+Denote <math>\frac {AD}{DE} = u, \frac {BE}{EF} = w, \frac {CF}{FD} = v.</math>
+<math>[DEF] = 1,</math> where <math>[X]</math> is the area of the figure <math>X.</math>
+<cmath>\frac {[ADF]}{[DEF]} = \frac {AD}{DE} = u, \frac {[ACF]}{[DEF]} = \frac {[ACF]}{[ADF]} \cdot \frac {[ADF]}{[DEF]} = uv.</cmath>
+Similarly, <cmath>\frac {[CFE]}{[DEF]} = v, \frac {[BCE]}{[DEF]} = vw, \frac {[BDE]}{[DEF]} = w, \frac {[ABD]}{[DEF]} = uw.</cmath>
+<cmath>\frac {[ABC]}{[DEF]} = 1 + u + v + w + uv + uw + vw = (1 + u)(1 + v)(1 + w) - uvw,</cmath>
+<cmath>\frac {[ABC]}{[DEF]}  = \frac {AE \cdot BF \cdot CD}{DE \cdot DF \cdot EF} -  \frac {AD \cdot BE \cdot CF}{DE \cdot DF \cdot EF}.</cmath>
+<cmath>\frac {DE \cdot DF \cdot EF}{4R} = [DEF] \implies</cmath>
+<cmath>[ABC] = \frac {AD \cdot BE \cdot CF}{4R} \cdot \left ( \frac {AE \cdot BF \cdot CD}{BE \cdot CF \cdot AD}-1 \right).</cmath>
+Similarly, <cmath>[ABC] = \frac {AE' \cdot BF' \cdot CD'}{4R'} \cdot \left ( \frac {AD' \cdot BE' \cdot CD}{AE' \cdot BF' \cdot CD'}-1 \right).</cmath>
+It is known that <math>\frac {AD}{AE} \cdot \frac {BE}{BF} \cdot \frac {CF}{CD} = \frac {AE'}{AD'} \cdot \frac {BF'}{BE'} \cdot \frac {CD'}{CF'}</math> ([[Isogonal_conjugate | Three pairs isogonal points]]), therefore
+<cmath>\frac {AD \cdot BE \cdot CF}{4R} = \frac {AE' \cdot BF' \cdot CD'}{4R'}.</cmath>
+Comment: The main idea of the proof was found by Leonid Shatunov.
+'''vladimir.shelomovskii@gmail.com, vvsss'''
 == Problems ==
+*[[File:1995 USAMO 3.png|300px|right]] Given a nonisosceles, nonright triangle <math>ABC,</math> let <math>O</math> denote the center of its circumscribed circle, and let <math>A_1, \, B_1,</math> and <math>C_1</math> be the midpoints of sides <math>BC, \, CA,</math> and <math>AB,</math> respectively. Point <math>A_2</math> is located on the ray <math>OA_1</math> so that <math>\triangle OAA_1</math> is similar to <math>\triangle OA_2A</math>. Points <math>B_2</math> and <math>C_2</math> on rays <math>OB_1</math> and <math>OC_1,</math> respectively, are defined similarly. Prove that lines <math>AA_2, \, BB_2,</math> and <math>CC_2</math> are concurrent. ([[1995 USAMO Problems/Problem 3|Source]])
+*[[File:2011 USAMO 5.png|400px|right]] Let <math>P</math> be a given point inside quadrilateral <math>ABCD</math>. Points <math>Q_1</math> and <math>Q_2</math> are located within <math>ABCD</math> such that <math>\angle Q_1 BC = \angle ABP</math>, <math>\angle Q_1 CB = \angle DCP</math>, <math>\angle Q_2 AD = \angle BAP</math>, <math>\angle Q_2 DA = \angle CDP</math>. Prove that <math>\overline{Q_1 Q_2} \parallel \overline{AB}</math> if and only if <math>\overline{Q_1 Q_2} \parallel \overline{CD}</math>. ([[2011 USAMO Problems/Problem 5|Source]])
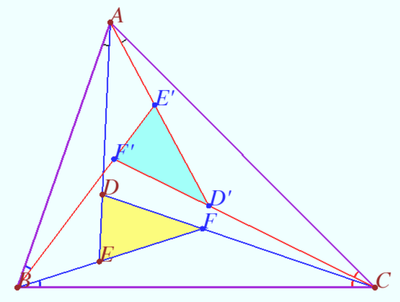
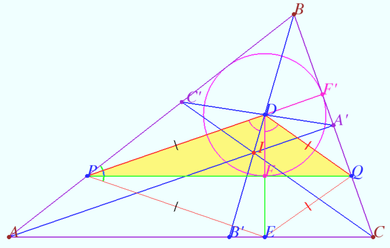
+*[[File:2024 16.png|390px|right]] Let <math>AA', BB',</math> and <math>CC'</math> be the bisectors of a triangle <math>\triangle ABC.</math>
+:The segments <math>BB'</math> and <math>A'C'</math> meet at point <math>D.</math> Let <math>E</math> be the projection of <math>D</math> to <math>AC.</math>
+:Points <math>P</math> and <math>Q</math> on the sides <math>AB</math> and <math>BC,</math> respectively, are such that <math>EP = PD, EQ = QD.</math>
+:Prove that <math>\angle PDB' = \angle EDQ.</math> ([[Sharygin_Olympiads,_the_best|Source]])
+*IMO 2007 Short list/G3
+[[File:Trapezoid 17.png|400px|right]]
+The diagonals of a trapezoid <math>ABCD</math> intersect at point <math>P.</math>
+Point <math>Q</math> lies between the parallel lines <math>BC</math> and <math>AD</math> such that <math>\angle AQD = \angle CQB,</math> and line <math>CD</math> separates points <math>P</math> and <math>Q.</math>
+Prove that <math>\angle BQP = \angle DAQ.</math>
+<i><b>Proof</b></i>
-=== Olympiad ===
+<math>\angle AQD = \angle CQB \implies</math>
-Given a nonisosceles, nonright triangle <math>ABC,</math> let <math>O</math> denote the center of its circumscribed circle, and let <math>A_1, \, B_1,</math> and <math>C_1</math> be the midpoints of sides <math>BC, \, CA,</math> and <math>AB,</math> respectively.  Point <math>A_2</math> is located on the ray <math>OA_1</math> so that <math>\triangle OAA_1</math> is similar to <math>\triangle OA_2A</math>.  Points <math>B_2</math> and <math>C_2</math> on rays <math>OB_1</math> and <math>OC_1,</math> respectively, are defined similarly.  Prove that lines <math>AA_2, \, BB_2,</math> and <math>CC_2</math> are concurrent, i.e. these three lines intersect at a point. ([[1995 USAMO Problems/Problem 3 |Source]])
+<math>BQ</math> and <math>AQ</math> are isogonals with respect <math>\angle CQD.</math>
+<math>P =AC \cap BD, BC || AD \implies</math>
+<math>QS || AD</math> is isogonal to <math>QP</math> with respect <math>\angle CQD.</math>
+From the converse of <i><b>The isogonal theorem</b></i> we get
+<math>\angle BQP = \angle SQA = \angle DAQ  \blacksquare</math>
+'''vladimir.shelomovskii@gmail.com, vvsss'''
-Let <math>P</math> be a given point inside quadrilateral <math>ABCD</math>.  Points <math>Q_1</math> and <math>Q_2</math> are located within <math>ABCD</math> such that <math>\angle Q_1 BC = \angle ABP</math>, <math>\angle Q_1 CB = \angle DCP</math>, <math>\angle Q_2 AD = \angle BAP</math>, <math>\angle Q_2 DA = \angle CDP</math>.  Prove that <math>\overline{Q_1 Q_2} \parallel \overline{AB}</math> if and only if <math>\overline{Q_1 Q_2} \parallel \overline{CD}</math>. ([[2011 USAMO Problems/Problem 5 |Source]])
 [[Category:Geometry]]
+<br>
+<br>
+{{stub}}

Page

Toolbox

Search

Difference between revisions of "Isogonal conjugate"

Latest revision as of 13:25, 7 August 2025

Contents

The isogonal theorem

Isogonal lines definition

Projective transformation

The isogonal theorem

Proof

The isogonal theorem in the case of parallel lines

Proof

Converse theorem

Proof

Parallel segments

Perpendicularity

Fixed point

Bisector

Isogonal of the diagonal of a quadrilateral

Isogonals in trapezium

Isogonals in complete quadrilateral

Isogonal of the bisector of the triangle

Points on isogonals

Trapezoid

Definition of isogonal conjugate of a point

Three points

Second definition

Distance to the sides of the triangle

Sign of isogonally conjugate points

Circumcircle of pedal triangles

Common circumcircle of the pedal triangles as the sign of isogonally conjugate points

Two pares of isogonally conjugate points

Circles

Equidistant isogonal conjugate points

Simplified distance formula for isogonal points

Point on circumcircle

Fixed point on circumcircle

Distance formula for isogonal points

Miquel point for isogonal conjugate points

Point on circumcircle

Simplified problem

Isogonal of line BC with respect to angle BAC

Isogonal bijection lines and points

Miquel point for two pare isogonal points

Isogonic center’s conjugate point

Three pairs isogonal points

Ratio for three pairs of isogonal points

Problems