Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2025 AIME I Problems/Problem 8"

(→‎Solution 1 (Systematic + Algebra))
m (→‎Solution 4)
 
(29 intermediate revisions by 3 users not shown)
Line 7: Line 7:
 
has exactly one complex solution <math>z</math>. The sum of all possible values of <math>k</math> can be written as <math>\frac{m}{n}</math>, where <math>m</math> and <math>n</math> are relatively prime positive integers. Find <math>m + n</math>. Here <math>i = \sqrt{-1}</math>.
 
has exactly one complex solution <math>z</math>. The sum of all possible values of <math>k</math> can be written as <math>\frac{m}{n}</math>, where <math>m</math> and <math>n</math> are relatively prime positive integers. Find <math>m + n</math>. Here <math>i = \sqrt{-1}</math>.
  
−
==Solution 1 (Systematic + Algebra)==
+
==Video solution by [[User:grogg007|grogg007]]==
 +
https://youtu.be/wib5vos7Sd4?t=268
 +
 
 +
==Solution 1==
 +
<asy>
 +
size(300);
 +
draw((0, 0) -- (0, 20), EndArrow(10));
 +
label("$y$", (0, 20), NW);
 +
dot((25,20));
 +
draw((0, 0) -- (25, 0), EndArrow(10));
 +
label("$x$", (25, 0), SE);
 +
draw(circle((25,20),5));
 +
label(scale(0.7)*"$(25,20)$", (25,20), S);
 +
draw((7,0) -- (3,3), blue);
 +
draw((5,3/2) -- (21,23), dashed);
 +
label("$(4+k,0)$", (7,0), S);
 +
label("$(k,3)$", (3,3), N);
 +
draw(rightanglemark((3,3),(5,3/2),(21,23), 20));
 +
draw(rightanglemark((25,20),(21,23),(5,3/2), 20));
 +
draw((25,20) -- (21,23));
 +
</asy>
 +
The complex number <math>z</math> must satisfy the following conditions on the complex plane:
 +
 
 +
<math>1.</math> The magnitude between <math>z</math> and <math>(25,20)</math> is <math>5.</math> This can be represented by drawing a circle with center <math>(25,20)</math> and radius <math>5.</math>
 +
 
 +
<math>2.</math> It is equidistant from the points <math>(4+k,0)</math> and <math>(k,3).</math> Hence it must lie on the perpendicular bisector of the line connecting these points.
 +
 
 +
 
 +
For <math>z</math> to have one solution, the perpendicular bisector of the segment connecting the two points must be tangent to the circle.
 +
This bisector must pass the midpoint, <math>(2+k,\frac{3}{2}),</math> and have slope <math>\frac{4}{3}.</math> The segment connecting the point of tangency to the center of the circle has slope <math>\frac{-3}{4},</math> meaning the points of tangency can be <math>(29,17)</math> or <math>(21,23).</math> Solving the equation for the slope of the perpendicular bisector gives <cmath>\frac{\frac{3}{2}-23}{k+2-21}=\frac{4}{3}</cmath> or <cmath>\frac{\frac{3}{2}-17}{k+2-29}=\frac{4}{3},</cmath> giving <math>k=\frac{23}{8}</math> or <math>\frac{123}{8}</math>, having a sum of <math>\frac{73}{4} \Longrightarrow \boxed{077}.</math>
 +
 
 +
~nevergonnagiveup
 +
 
 +
==Solution 2 (Systematic + Algebra)==
 
We first look at each equation, and we convert each to algebra (note that the absolute value sign of <math>|</math> means the magnitude). Let's convert z to <math>A + Bi</math>.
 
We first look at each equation, and we convert each to algebra (note that the absolute value sign of <math>|</math> means the magnitude). Let's convert z to <math>A + Bi</math>.
  
Line 32: Line 65:
 
This equation can be seen as a line with a <math>\frac{4}{3}</math> slope, and a y-intercept of <math>\frac{4}{3}k - \frac{7}{6}</math>.  
 
This equation can be seen as a line with a <math>\frac{4}{3}</math> slope, and a y-intercept of <math>\frac{4}{3}k - \frac{7}{6}</math>.  
  
−
Note that the question only wants one solution, so we want two tangent lines, one above the circle, and one below the circle. You can see Solution 1 for the picture.
+
Note that the question only wants one solution, so we want two tangent lines, one above the circle, and one below the circle. You can see Solution 2 for the picture.
  
 
Because the slope is <math>\frac{4}{3}</math>, the circle must have a slope coming out of center of its reciprocal, <math>-\frac{3}{4}</math>. So the points on the circle where this line with a <math>\frac{4}{3}</math> must intersect must be <math>(21, 23)</math> and <math>(29, 17)</math>. We can easily use point-slope form to find the equations of these lines.  
 
Because the slope is <math>\frac{4}{3}</math>, the circle must have a slope coming out of center of its reciprocal, <math>-\frac{3}{4}</math>. So the points on the circle where this line with a <math>\frac{4}{3}</math> must intersect must be <math>(21, 23)</math> and <math>(29, 17)</math>. We can easily use point-slope form to find the equations of these lines.  
−
<math></math>y - 23 = \frac{4}{3}(x - 21)<math> </math>
+
<cmath>y - 23 = \frac{4}{3}(x - 21)</cmath>
  
 
and  
 
and  
Line 52: Line 85:
  
 
~Marcus :)
 
~Marcus :)
−
 
−
==Solution 2==
 
−
<asy>
 
−
size(300);
 
−
draw((0, 0) -- (0, 20), EndArrow(10));
 
−
label("$y$", (0, 20), NW);
 
−
dot((25,20));
 
−
draw((0, 0) -- (25, 0), EndArrow(10));
 
−
label("$x$", (25, 0), SE);
 
−
draw(circle((25,20),5));
 
−
label(scale(0.7)*"$(25,20)$", (25,20), S);
 
−
draw((7,0) -- (3,3), blue);
 
−
draw((5,3/2) -- (21,23), dashed);
 
−
label("$(4+k,0)$", (7,0), S);
 
−
label("$(k,3)$", (3,3), N);
 
−
draw(rightanglemark((3,3),(5,3/2),(21,23), 20));
 
−
draw(rightanglemark((25,20),(21,23),(5,3/2), 20));
 
−
draw((25,20) -- (21,23));
 
−
</asy>
 
−
The complex number <math>z</math> must satisfy the following conditions on the complex plane:
 
−
 
−
<math>1.</math> The magnitude between <math>z</math> and <math>(25,20)</math> is <math>5.</math> This can be represented by drawing a circle with center <math>(25,20)</math> and radius <math>5.</math>
 
−
 
−
<math>2.</math> It is equidistant from the points <math>(4+k,0)</math> and <math>(k,3).</math> Hence it must lie on the perpendicular bisector of the line connecting these points.
 
−
 
−
 
−
For <math>z</math> to have one solution, the perpendicular bisector of the segment connecting the two points must be tangent to the circle.
 
−
This bisector must pass the midpoint, <math>(2+k,\frac{3}{2}),</math> and have slope <math>\frac{4}{3}.</math> The segment connecting the point of tangency to the center of the circle has slope <math>\frac{-3}{4},</math> meaning the points of tangency can be <math>(29,17)</math> or <math>(21,23).</math> Solving the equation for the slope of the perpendicular bisector gives <cmath>\frac{\frac{3}{2}-23}{k+2-21}=\frac{4}{3}</cmath> or <cmath>\frac{\frac{3}{2}-17}{k+2-29}=\frac{4}{3},</cmath> giving <math>k=\frac{23}{8}</math> or <math>\frac{123}{8}</math>, having a sum of <math>\frac{73}{4} \Longrightarrow \boxed{077}.</math>
 
−
 
−
~nevergonnagiveup
 
−
 
−
 
−
 
−
There's actually an easier way to do it using this method by utilizing the distance between point and line formula after building off of what is shown above.
 
−
First we find the standard form of the perpendicular bisector, which can be found using the point-slope form: <math>y-b = m(x-a)</math>, where <math>a</math> and <math>b</math> are the <math>x</math> and <math>y</math> coordinates of a point on the line. By plugging in <math>(2+k, \frac{3}{2})</math>, we get <math>y-\frac{3}{2} = \frac{4}{3}(x-2-k)</math>, we can eventually find the standard form as <math>8x-6y-7-8k=0</math>.
 
−
Now we use the distance between point and line formula on the center of the circle at <math>(25, 20)</math> and the perpendicular bisector.
 
−
We get <math>d = \frac{|8\cdot 25-6\cdot 20-7-8k|}{\sqrt{6^2+8^2}}</math>. Plugging in <math>d</math> = 5 we can simplify this to <math>50 = |200-120-7-8k|</math>. We can finally solve for the absolute value equality and figure out <math>k = \frac{23}{8}</math> or <math>k = \frac{123}{8}</math>. Adding them together, we get <math>\frac{146}{8} = \frac{73}{4}</math>, hence the answer which we desire is <math>\Longrightarrow \boxed{077}.</math>
 
−
 
−
~Mathycoder (edited by MathKing555)
 
  
 
==Solution 3 (A Little Geometry)==
 
==Solution 3 (A Little Geometry)==
Line 121: Line 115:
  
 
~cassphe
 
~cassphe
 +
 +
 +
==Solution 4 (Distance Formula)==
 +
Let <math>z = a + bi.</math> Then the system becomes <math>(25 - a)^2 + (20 - b)^2 = 25</math> and <math>(a - 4 - k)^2 + b^2 = (a - k)^2 + (b - 3)^2</math> <math>\implies b = \frac{4}{3}a - (\frac{4}{3}k + \frac{7}{6})</math>. For this system to have one solution for <math>z,</math> the line <math>b = \frac{4}{3}a - (\frac{4}{3}k + \frac{7}{6})</math> must be tangent to the circle <math>(25 - a)^2 + (20 - b)^2 = 25</math>. For a line to be tangent to a circle, the distance between the line and center must be equal to the length of the radius, which is <math>5</math>. The center of the circle is <math>(a,b) \rightarrow (25,20),</math> and we can express the line as <math>8a - 6b - (8k + 7) = 0.</math> So we have: <cmath>d = \frac{|Ax_0 + By_0 + C|}{\sqrt{A^2 + B^2}} = \frac{|8(25) - 6(20) -(8k + 7)|}{\sqrt{8^2 + 6^2}} =  \frac{|73 - 8k|}{10} = 5 \implies |73 - 8k| = 50</cmath>  <cmath>k = \frac{23}{8}, \frac{123}{8}.</cmath> <math>\frac{m}{n}</math> is <math>\frac{146}{8} = \frac{73}{4}.</math> The requested sum is <math>73 + 4 = \boxed{77}.</math>
 +
 +
~[[User:grogg007|grogg007]], Mathycoder & MathKing555 also previously mentioned a similar approach
  
 
==See also==
 
==See also==

Latest revision as of 21:44, 10 August 2025

Problem

Let $k$ be a real number such that the system \begin{align*} &|25 + 20i - z| = 5 \\ &|z - 4 - k| = |z - 3i - k| \end{align*} has exactly one complex solution $z$. The sum of all possible values of $k$ can be written as $\frac{m}{n}$, where $m$ and $n$ are relatively prime positive integers. Find $m + n$. Here $i = \sqrt{-1}$.

Video solution by grogg007

https://youtu.be/wib5vos7Sd4?t=268

Solution 1

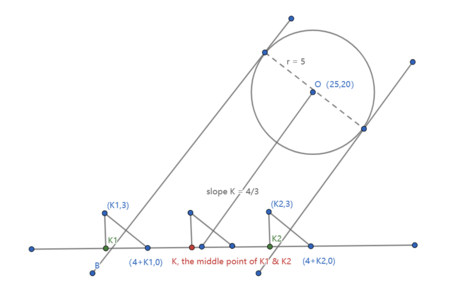
[asy] size(300); draw((0, 0) -- (0, 20), EndArrow(10)); label("$y$", (0, 20), NW); dot((25,20)); draw((0, 0) -- (25, 0), EndArrow(10)); label("$x$", (25, 0), SE); draw(circle((25,20),5)); label(scale(0.7)*"$(25,20)$", (25,20), S); draw((7,0) -- (3,3), blue); draw((5,3/2) -- (21,23), dashed); label("$(4+k,0)$", (7,0), S); label("$(k,3)$", (3,3), N); draw(rightanglemark((3,3),(5,3/2),(21,23), 20)); draw(rightanglemark((25,20),(21,23),(5,3/2), 20)); draw((25,20) -- (21,23)); [/asy] The complex number $z$ must satisfy the following conditions on the complex plane:

$1.$ The magnitude between $z$ and $(25,20)$ is $5.$ This can be represented by drawing a circle with center $(25,20)$ and radius $5.$

$2.$ It is equidistant from the points $(4+k,0)$ and $(k,3).$ Hence it must lie on the perpendicular bisector of the line connecting these points.


For $z$ to have one solution, the perpendicular bisector of the segment connecting the two points must be tangent to the circle. This bisector must pass the midpoint, $(2+k,\frac{3}{2}),$ and have slope $\frac{4}{3}.$ The segment connecting the point of tangency to the center of the circle has slope $\frac{-3}{4},$ meaning the points of tangency can be $(29,17)$ or $(21,23).$ Solving the equation for the slope of the perpendicular bisector gives \[\frac{\frac{3}{2}-23}{k+2-21}=\frac{4}{3}\] or \[\frac{\frac{3}{2}-17}{k+2-29}=\frac{4}{3},\] giving $k=\frac{23}{8}$ or $\frac{123}{8}$, having a sum of $\frac{73}{4} \Longrightarrow \boxed{077}.$

~nevergonnagiveup

Solution 2 (Systematic + Algebra)

We first look at each equation, and we convert each to algebra (note that the absolute value sign of $|$ means the magnitude). Let's convert z to $A + Bi$.


Note that the first equation becomes: $(25 - A)^2 + (20 - B)^2 = 25$

Note that this is the equation of a circle centered at $(25, 20)$ with radius $5$.


And the second equation becomes: $(A-4-k)^2 + B^2 = (A - k)^2 + (B-3)^2$

You can see that the many similar terms that cancel out, simplfying, you get:

$-8(A - k) + 16 + 6B = 9$

Now we must isolate B

\[B= \frac{4}{3}(A-k) - \frac{7}{6}\]

\[B = \frac{4}{3}A - \frac{4}{3}k - \frac{7}{6}\]

This equation can be seen as a line with a $\frac{4}{3}$ slope, and a y-intercept of $\frac{4}{3}k - \frac{7}{6}$.

Note that the question only wants one solution, so we want two tangent lines, one above the circle, and one below the circle. You can see Solution 2 for the picture.

Because the slope is $\frac{4}{3}$, the circle must have a slope coming out of center of its reciprocal, $-\frac{3}{4}$. So the points on the circle where this line with a $\frac{4}{3}$ must intersect must be $(21, 23)$ and $(29, 17)$. We can easily use point-slope form to find the equations of these lines. \[y - 23 = \frac{4}{3}(x - 21)\]

and

\[y - 17 = \frac{4}{3}(x - 29)\]

Now we must match the y-intercepts to the equations with $k$ in it. Solving the equations:

\[\frac{4}{3}(-21) + 23 = - \frac{4}{3}k - \frac{7}{6}\]

\[\frac{4}{3}(-29) + 17 = - \frac{4}{3}k - \frac{7}{6}\]

we get that $k = \frac{23}{8}$ and $k = \frac{123}{8}$ Adding them up and simplifying, we get a sum of $\frac{73}{4} \Longrightarrow \boxed{077}.$

~Marcus :)

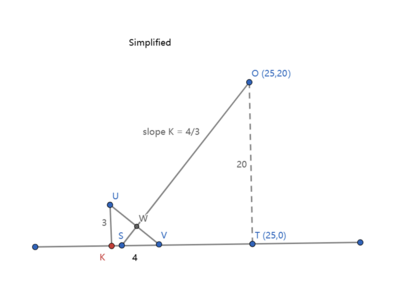
Solution 3 (A Little Geometry)

2025AIMEII P8 Solution3 1.png2025AIMEII P8 Solution3 2.png

To solve the problem, we first locate the point $Z$. According to the conditions, we can know that:

$Z$ is on the perpendicular bisector of $(k,3)$ and $(k+4,0)$

The distance from $Z$ to circle $O(25,20)$ is ${5}$.

Therefore, $Z$ must be the 2 points of tangent of a line with the slope of $\frac{4}{3}$ with circle O (center at $(25,20)$, radius of ${5}$), corresponding to the 2 values: ${K_1}$ and ${K_2}$.

Since the question only asks for the sum of ${K_1}$ and ${K_2}$, we would not need to calculate them separately. Let the middle point of ${K_1}$ and ${K_2}$ be ${K}$ ==> ${K_1}$ + ${K_2}$ = ${2K}$.

Looking at the simplified figure below. We may calculate using similarity of the triangles:

$\frac{SV}{SO}=\frac{WV}{OT}$

$SV = \frac{2.5\cdot25}{20}=\frac{25}{8}$

$KS = KV-SV = 4-\frac{25}{8} = \frac{7}{8}$

$KT = KS+ST = \frac{7}{8}+15 = \frac{127}{8}$

$K_1+K_2 = 2K = (25-\frac{127}{8})\cdot2= \frac{73}{8}\cdot2 = \frac{73}{4}$

We conclude that $m+n=\boxed{077}$.

~cassphe


Solution 4 (Distance Formula)

Let $z = a + bi.$ Then the system becomes $(25 - a)^2 + (20 - b)^2 = 25$ and $(a - 4 - k)^2 + b^2 = (a - k)^2 + (b - 3)^2$ $\implies b = \frac{4}{3}a - (\frac{4}{3}k + \frac{7}{6})$. For this system to have one solution for $z,$ the line $b = \frac{4}{3}a - (\frac{4}{3}k + \frac{7}{6})$ must be tangent to the circle $(25 - a)^2 + (20 - b)^2 = 25$. For a line to be tangent to a circle, the distance between the line and center must be equal to the length of the radius, which is $5$. The center of the circle is $(a,b) \rightarrow (25,20),$ and we can express the line as $8a - 6b - (8k + 7) = 0.$ So we have: \[d = \frac{|Ax_0 + By_0 + C|}{\sqrt{A^2 + B^2}} = \frac{|8(25) - 6(20) -(8k + 7)|}{\sqrt{8^2 + 6^2}} = \frac{|73 - 8k|}{10} = 5 \implies |73 - 8k| = 50\] \[k = \frac{23}{8}, \frac{123}{8}.\] $\frac{m}{n}$ is $\frac{146}{8} = \frac{73}{4}.$ The requested sum is $73 + 4 = \boxed{77}.$

~grogg007, Mathycoder & MathKing555 also previously mentioned a similar approach

See also

2025 AIME I (Problems • Answer Key • Resources)
Preceded by
Problem 7 		Followed by
Problem 9
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. AMC Logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2025_AIME_I_Problems/Problem_8&oldid=257004"