Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2021 USAMO Problems/Problem 1"

(→‎Solution: SEVERE LaTeX formatting fixing)
 
Line 1: Line 1:
−
Rectangles <math>BCC_1B_2,</math> <math>CAA_1C_2,</math> and <math>ABB_1A_2</math> are erected outside an acute triangle <math>ABC.</math> Suppose that<cmath>\angle BC_1C+\angle CA_1A+\angle AB_1B=180^{\circ}.</cmath>Prove that lines <math>B_1C_2,</math> <math>C_1A_2,</math> and <math>A_1B_2</math> are concurrent.
+
==Problem==
 +
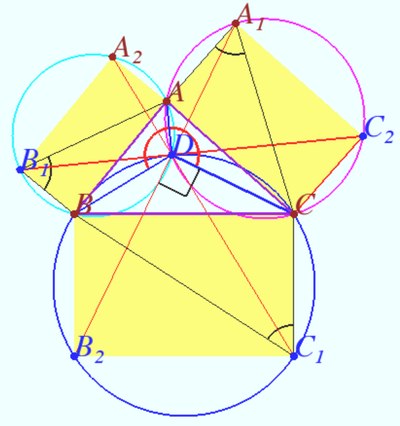
Rectangles <math>BCC_{1}B_{2}</math>, <math>CAA_{1}C_{2}</math>, and <math>ABB_{1}A_{2}</math> are erected outside an acute triangle <math>ABC</math>. Suppose that <cmath>\angle BC_{1}C + \angle CA_{1}A + \angle AB_{1}B = 180^{\circ}.</cmath> Prove that lines <math>B_{1}C_{2}</math>, <math>C_{1}A_{2}</math>, and <math>A_{1}B_{2}</math> are concurrent.
  
 
==Solution==
 
==Solution==
Line 20: Line 21:
 
'''vladimir.shelomovskii@gmail.com, vvsss'''
 
'''vladimir.shelomovskii@gmail.com, vvsss'''
  
 +
==Video Solution==
 +
https://youtube.com/watch?v=6e_IGnpQGEg
 +
 +
==See also==
 +
{{USAMO newbox|year=2021|before=First Problem|num-a=2}}
 +
{{USAJMO newbox|year=2021|num-b=1|num-a=3}}
 +
[[Category:Olympiad Geometry Problems]]
 
{{MAA Notice}}
 
{{MAA Notice}}

Latest revision as of 13:21, 1 September 2025

Problem

Rectangles $BCC_{1}B_{2}$, $CAA_{1}C_{2}$, and $ABB_{1}A_{2}$ are erected outside an acute triangle $ABC$. Suppose that \[\angle BC_{1}C + \angle CA_{1}A + \angle AB_{1}B = 180^{\circ}.\] Prove that lines $B_{1}C_{2}$, $C_{1}A_{2}$, and $A_{1}B_{2}$ are concurrent.

Solution

2021 USAMO 1.png

Let $D$ be the second point of intersection of the circles $AB_1B$ and $AA_1C.$ Then: \begin{align*} \angle ADB &= 180^\circ – \angle AB_1B,&\angle ADC &= 180^\circ – \angle AA_1C\\ \angle BDC &= 360^\circ – \angle ADB – \angle ADC\\ &= 360^\circ – (180^\circ – \angle AB_1B) – (180^\circ – \angle AA_1C)\\ &= \angle AB_1B + \angle AA_1C\\ \angle BDC + \angle BC_1C &= 180^\circ \end{align*} Therefore, $BDCC_1B_2$ is cyclic with diameters $BC_1$ and $CB_2$, and thus $\angle CDB_2 = 90^\circ.$ Similarly, $\angle CDA_1 = 90^\circ$, meaning points $A_1$, $D$, and $B_2$ are collinear.

Similarly, the points $A_2, D, C_1$ and $C_2, D, B_1$ are collinear.

(After USAMO 2021 Solution Notes – Evan Chen)

vladimir.shelomovskii@gmail.com, vvsss

Video Solution

https://youtube.com/watch?v=6e_IGnpQGEg

See also

2021 USAMO (Problems • Resources)
Preceded by
First Problem 		Followed by
Problem 2
1 • 2 • 3 • 4 • 5 • 6
All USAMO Problems and Solutions
2021 USAJMO (Problems • Resources)
Preceded by
Problem 1 		Followed by
Problem 3
1 • 2 • 3 • 4 • 5 • 6
All USAJMO Problems and Solutions

These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. AMC Logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2021_USAMO_Problems/Problem_1&oldid=259524"