Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2020 USAMO Problems/Problem 1"

(→‎Video Solution)
 
(4 intermediate revisions by one other user not shown)
Line 18: Line 18:
  
 
The area of <math>\triangle OO_1O_2</math> is minimized if <math>CX \perp AB</math> because
 
The area of <math>\triangle OO_1O_2</math> is minimized if <math>CX \perp AB</math> because
−
<math></math>\frac {[OO_1O_2]} {[ABC]} = (\frac {O_1 O_2} {AB})^2 \ge (\frac {EF} {AB})^2 = \frac {1}{4}$.  
+
<cmath>\frac {[OO_1O_2]} {[ABC]} = \left(\frac {O_1 O_2} {AB}\right)^2 \ge \left(\frac {EF} {AB}\right)^2 = \frac {1}{4}.</cmath>
−
 
+
'''vladimir.shelomovskii@gmail.com, vvsss'''
−
 
 
  
 +
==Video Solution 1==
 +
https://www.youtube.com/watch?v=m157cfw0vdE
  
 +
==Video Solution 2==
 +
https://youtube.com/watch?v=HLNb_4KmayA
  
−
==Video Solution==
+
==See also==
−
https://www.youtube.com/watch?v=m157cfw0vdE
+
{{USAMO newbox|year=2020|before=First Problem|num-a=2}}
 +
{{MAA Notice}}

Latest revision as of 13:42, 1 September 2025

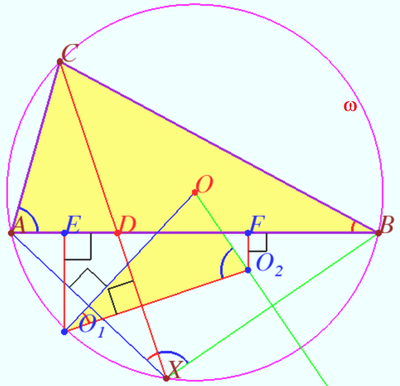
Problem 1

Let $ABC$ be a fixed acute triangle inscribed in a circle $\omega$ with center $O$. A variable point $X$ is chosen on minor arc $AB$ of $\omega$, and segments $CX$ and $AB$ meet at $D$. Denote by $O_1$ and $O_2$ the circumcenters of triangles $ADX$ and $BDX$, respectively. Determine all points $X$ for which the area of triangle $OO_1O_2$ is minimized.


Solution

2020 USAMO 1.png

Let $E$ be midpoint $AD.$ Let $F$ be midpoint $BD \implies$ \[EF = ED + FD = \frac {AD}{2} + \frac {BD}{2} = \frac {AB}{2}.\] $E$ and $F$ are the bases of perpendiculars dropped from $O_1$ and $O_2,$ respectively.

Therefore $O_1O_2 \ge EF = \frac {AB}{2}.$

\[CX \perp O_1O_2, AX \perp O_1O \implies \angle O O_1O_2 = \angle AXC\] $\angle AXC = \angle ABC (AXBC$ is cyclic) $\implies \angle O O_1O_2 = \angle ABC.$

Similarly $\angle BAC = \angle O O_2 O_1 \implies \triangle ABC \sim \triangle O_2 O_1O.$

The area of $\triangle OO_1O_2$ is minimized if $CX \perp AB$ because \[\frac {[OO_1O_2]} {[ABC]} = \left(\frac {O_1 O_2} {AB}\right)^2 \ge \left(\frac {EF} {AB}\right)^2 = \frac {1}{4}.\] vladimir.shelomovskii@gmail.com, vvsss

Video Solution 1

https://www.youtube.com/watch?v=m157cfw0vdE

Video Solution 2

https://youtube.com/watch?v=HLNb_4KmayA

See also

2020 USAMO (Problems • Resources)
Preceded by
First Problem 		Followed by
Problem 2
1 • 2 • 3 • 4 • 5 • 6
All USAMO Problems and Solutions

These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. AMC Logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2020_USAMO_Problems/Problem_1&oldid=259526"