Difference between revisions of "2007 AMC 12A Problems/Problem 10"
(→Solution) |
(→Solution 4) |
||
| (24 intermediate revisions by 7 users not shown) | |||
| Line 1: | Line 1: | ||
| + | {{duplicate|[[2007 AMC 12A Problems|2007 AMC 12A #10]] and [[2007 AMC 10A Problems/Problem 14|2007 AMC 10A #14]]}} | ||
| + | |||
==Problem== | ==Problem== | ||
| − | A [[triangle]] with side lengths in the [[ratio]] <math>3 : 4 : 5</math> is inscribed in a [[circle]] with [[radius]] 3. What | + | A [[triangle]] with side lengths in the [[ratio]] <math>3 : 4 : 5</math> is inscribed in a [[circle]] with [[radius]] 3. What is the area of the triangle? |
<math>\mathrm{(A)}\ 8.64\qquad \mathrm{(B)}\ 12\qquad \mathrm{(C)}\ 5\pi\qquad \mathrm{(D)}\ 17.28\qquad \mathrm{(E)}\ 18</math> | <math>\mathrm{(A)}\ 8.64\qquad \mathrm{(B)}\ 12\qquad \mathrm{(C)}\ 5\pi\qquad \mathrm{(D)}\ 17.28\qquad \mathrm{(E)}\ 18</math> | ||
| Line 8: | Line 10: | ||
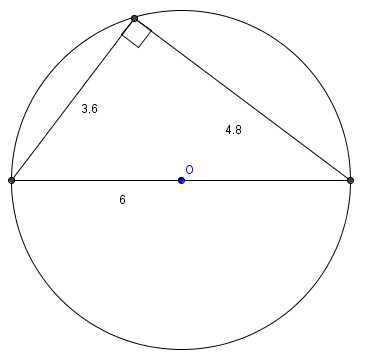
Since 3-4-5 is a [[Pythagorean triple]], the triangle is a [[right triangle]]. Since the hypotenuse is a [[diameter]] of the [[circumcircle]], the hypotenuse is <math>2r = 6</math>. Then the other legs are <math>\frac{24}5=4.8</math> and <math>\frac{18}5=3.6</math>. The area is <math>\frac{4.8 \cdot 3.6}2 = 8.64\ \mathrm{(A)}</math> | Since 3-4-5 is a [[Pythagorean triple]], the triangle is a [[right triangle]]. Since the hypotenuse is a [[diameter]] of the [[circumcircle]], the hypotenuse is <math>2r = 6</math>. Then the other legs are <math>\frac{24}5=4.8</math> and <math>\frac{18}5=3.6</math>. The area is <math>\frac{4.8 \cdot 3.6}2 = 8.64\ \mathrm{(A)}</math> | ||
| + | |||
| + | ==Solution 2== | ||
| + | The hypotenuse of the triangle is a diameter of the circumcircle, so it has length <math>2 \cdot 3 = 6</math>. The triangle is similar to a 3-4-5 triangle with the ratio of their side lengths equal to <math>\frac{6}{5}</math>. The area of a 3-4-5 triangle is <math>\frac{3\cdot 4}{2} = 6</math>. | ||
| + | The square of the ratio of their side lengths is equal to the ratio of their areas. Call the area of the triangle <math>A</math>. Therefore, <math>\left(\frac{6}{5}\right)^2 = \frac{A}{6} \Longrightarrow \frac{36}{25} = \frac{A}{6} \Longrightarrow A = \frac{36\cdot6}{25} = 8.64\ \mathrm{(A)}</math> | ||
| + | |||
| + | ~mobius247 | ||
| + | |||
| + | ==Solution 3 (dimensional analysis)== | ||
| + | Using the theorem that the hypotenuse of a right triangle inscribed in a circle is the diameter, one can determine that the diameter of the triangle is 6. As a result the ratio between the triangular ratios and their real values is (6/5). Using dimensional analysis, one can see that because the ratio between lengths is (6/5), the ratio between areas is (6/5)^2. This gives ((3 * 4)(6/5)^2)/2 as the area of the triangle or answer choice (A). | ||
| + | |||
| + | ==Solution 4== | ||
| + | Let the sides of the triangle be <math>3x, 4x, 5x</math> for some <math>x</math>. Now use the fact that the area of a triangle is equal to <math>\frac{abc}{4R}</math>, where <math>a, b, c</math> are side lengths and <math>R</math> is the circumradius. Also note that due to the 3, 4, 5 triple, the triangle is right. Thus we get <math>\frac{12x^2}{2} = \frac{60x^3}{4\cdot 3}\Rightarrow x = \frac{6}{5} = 1.2</math>. Then the area is <math>12(1.2)^2/2 = \boxed{8.64 \text{ (A)}}</math>. | ||
==See also== | ==See also== | ||
{{AMC12 box|year=2007|ab=A|num-b=9|num-a=11}} | {{AMC12 box|year=2007|ab=A|num-b=9|num-a=11}} | ||
| + | {{AMC10 box|year=2007|ab=A|num-b=13|num-a=15}} | ||
[[Category:Introductory Geometry Problems]] | [[Category:Introductory Geometry Problems]] | ||
| + | [[Category:Area Problems]] | ||
| + | {{MAA Notice}} | ||
Latest revision as of 04:47, 2 October 2025
- The following problem is from both the 2007 AMC 12A #10 and 2007 AMC 10A #14, so both problems redirect to this page.
Contents
Problem
A triangle with side lengths in the ratio 
is inscribed in a circle with radius 3. What is the area of the triangle?
Solution
Since 3-4-5 is a Pythagorean triple, the triangle is a right triangle. Since the hypotenuse is a diameter of the circumcircle, the hypotenuse is 
. Then the other legs are 
and 
. The area is 
Solution 2
The hypotenuse of the triangle is a diameter of the circumcircle, so it has length 
. The triangle is similar to a 3-4-5 triangle with the ratio of their side lengths equal to 
. The area of a 3-4-5 triangle is 
.
The square of the ratio of their side lengths is equal to the ratio of their areas. Call the area of the triangle 
. Therefore, 
~mobius247
Solution 3 (dimensional analysis)
Using the theorem that the hypotenuse of a right triangle inscribed in a circle is the diameter, one can determine that the diameter of the triangle is 6. As a result the ratio between the triangular ratios and their real values is (6/5). Using dimensional analysis, one can see that because the ratio between lengths is (6/5), the ratio between areas is (6/5)^2. This gives ((3 * 4)(6/5)^2)/2 as the area of the triangle or answer choice (A).
Solution 4
Let the sides of the triangle be 
for some 
. Now use the fact that the area of a triangle is equal to 
, where 
are side lengths and 
is the circumradius. Also note that due to the 3, 4, 5 triple, the triangle is right. Thus we get 
. Then the area is 
.
See also
| 2007 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 9 |
Followed by Problem 11 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
| 2007 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by Problem 13 |
Followed by Problem 15 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. 
