Difference between revisions of "2007 AMC 12A Problems/Problem 6"
(→Solution 2) |
|||
| Line 15: | Line 15: | ||
==Solution 2== | ==Solution 2== | ||
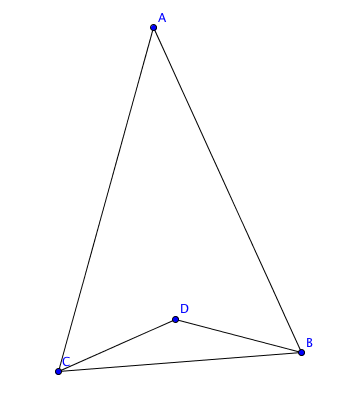
[[File:Mihir_Borkar_Solution_2007_AMC_10A_Problem_6.png]] | [[File:Mihir_Borkar_Solution_2007_AMC_10A_Problem_6.png]] | ||
| + | |||
| + | Since triangle <math>ABC</math> is isosceles we know that angle <math>\angle BAC = \angle BCA</math>. | ||
| + | |||
| + | Also since triangle <math>ADC</math> is isosceles we know that <math>\angle DAC = \angle DCA</math>. | ||
| + | |||
| + | This implies that <math>\angle BAD = \angle BCD</math>. | ||
| + | |||
| + | Then the sum of the angles in quadrilateral <math>ABCD</math> is <math>40 + 220 + 2\angle BAD = 40 + 220 + 2\angle BCD = 360</math>. | ||
==See also== | ==See also== | ||
Revision as of 19:00, 10 August 2014
- The following problem is from both the 2007 AMC 12A #6 and 2007 AMC 10A #8, so both problems redirect to this page.
Contents
Problem
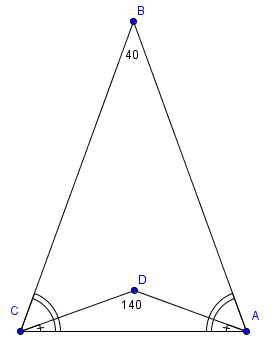
Triangles 
and 
are isosceles with 
and 
. Point 
is inside triangle , angle measures 40 degrees, and angle measures 140 degrees. What is the degree measure of angle 
?
Solution 1
We angle chase, and find out that:
Solution 2
Since triangle is isosceles we know that angle 
.
Also since triangle is isosceles we know that 
.
This implies that 
.
Then the sum of the angles in quadrilateral 
is 
.
See also
| 2007 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 5 |
Followed by Problem 7 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
| 2007 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by Problem 7 |
Followed by Problem 9 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. 
