Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "1977 Canadian MO Problems"

m (→‎Problem 7)
m (→‎Problem 7)
 
(6 intermediate revisions by one other user not shown)
Line 3: Line 3:
 
== Problem 1 ==
 
== Problem 1 ==
  
−
If <math>\displaystyle f(x)=x^2+x,</math> prove that the equation <math>\displaystyle 4f(a)=f(b)</math> has no solutions in positive integers <math>\displaystyle a</math> and <math>\displaystyle b.</math>
+
If <math>f(x)=x^2+x,</math> prove that the equation <math>4f(a)=f(b)</math> has no solutions in positive integers <math>a</math> and <math>b.</math>
  
 
[[1977 Canadian MO Problems/Problem 1 | Solution]]
 
[[1977 Canadian MO Problems/Problem 1 | Solution]]
Line 9: Line 9:
 
== Problem 2 ==
 
== Problem 2 ==
  
−
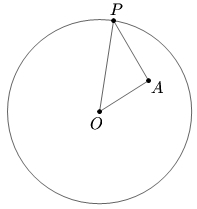
Let <math>\displaystyle O</math> be the center of a circle and <math>\displaystyle A</math> be a fixed interior point of the circle different from <math>\displaystyle O.</math> Determine all points <math>\displaystyle P</math> on the circumference of the circle such that the angle <math> \displaystyle OPA</math> is a maximum.  
+
Let <math>O</math> be the center of a circle and <math>A</math> be a fixed interior point of the circle different from <math>O.</math> Determine all points <math>P</math> on the circumference of the circle such that the angle <math>OPA</math> is a maximum.  
  
 
[[Image:CanadianMO-1977-2.jpg]]
 
[[Image:CanadianMO-1977-2.jpg]]
Line 18: Line 18:
 
== Problem 3 ==
 
== Problem 3 ==
  
−
<math>\displaystyle N</math> is an integer whose representation in base <math>\displaystyle b</math> is <math>\displaystyle 777.</math> Find the smallest positive integer <math>\displaystyle b</math> for which <math>\displaystyle N</math> is the fourth power of an integer.
+
<math>N</math> is an integer whose representation in base <math>b</math> is <math>777.</math> Find the smallest positive integer <math>b</math> for which <math>N</math> is the fourth power of an integer.
  
 
[[1977 Canadian MO Problems/Problem 3 | Solution]]
 
[[1977 Canadian MO Problems/Problem 3 | Solution]]
Line 36: Line 36:
  
 
== Problem 5 ==
 
== Problem 5 ==
 +
 +
A right circular cone of base radius <math>1</math> cm and slant height of <math>3</math> cm is given. <math>P</math> is a point on the circumference of
 +
the base and the shortest path from <math>P</math> around the cone is drawn (see diagram). What is the minimum distance from
 +
the vertex <math>V</math> to this path?
 +
 +
<asy>
 +
path p1=yscale(.25)*arc((0,0),1,0,180);
 +
path p2=yscale(.25)*arc((0,0),1,0,-180);
 +
path q1=shift(-.25,.4)*rotate(30)*xscale(.85)*p1;
 +
path q2=shift(-.25,.4)*rotate(30)*xscale(.85)*p2;
 +
draw(p2,black);draw(q2,black);
 +
draw(p1,dashed);draw(q1,dashed);
 +
draw((-1,0)--(-.5,2.4)--(1,0));
 +
MP("P",(-1,0),W);MP("V",(-.5,2.4),N);
 +
draw((-.2,2.5)--(1.2,.2),arrow=ArcArrow());
 +
draw((1.2,.2)--(-.2,2.5),arrow=ArcArrow());
 +
draw((0,0)--(1,0),arrow=ArcArrow());
 +
draw((1,0)--(0,0),arrow=ArcArrow());
 +
MP("1 cm",(.5,.04),S);MP("3 cm",(.5,1.35),NE);
 +
</asy>
 +
  
 
[[1977 Canadian MO Problems/Problem 5 | Solution]]
 
[[1977 Canadian MO Problems/Problem 5 | Solution]]
Line 52: Line 73:
 
to work each day but, on any given trip, she makes sure that her path does not include any intersection
 
to work each day but, on any given trip, she makes sure that her path does not include any intersection
 
twice. Show that the number <math>f(m,n)</math> of different paths  she can take to work satisfies <math>f(m,n)\le 2^{mn}</math>.
 
twice. Show that the number <math>f(m,n)</math> of different paths  she can take to work satisfies <math>f(m,n)\le 2^{mn}</math>.
 +
 +
<cmath>\underbrace{ \left. \begin{array}{|c|c|c|c|c|c|c|c|c|c|c| }
 +
    \hline
 +
    &&&&&&&&&& \\ \hline
 +
    &&&&&&&&&& \\ \hline
 +
    &&&&&&&&&& \\ \hline
 +
    &&&&&&&&&& \\ \hline
 +
    &&&&&&&&&& \\ \hline
 +
    &&&&&&&&&& \\ \hline
 +
    &&&&&&&&&& \\ \hline
 +
\end{array}
 +
\right\}n}_m</cmath>
  
 
[[1977 Canadian MO Problems/Problem 7 | Solution]]
 
[[1977 Canadian MO Problems/Problem 7 | Solution]]

Latest revision as of 19:23, 10 March 2015

The seven problems were all on the same day.

Problem 1

If $f(x)=x^2+x,$ prove that the equation $4f(a)=f(b)$ has no solutions in positive integers $a$ and $b.$

Solution

Problem 2

Let $O$ be the center of a circle and $A$ be a fixed interior point of the circle different from $O.$ Determine all points $P$ on the circumference of the circle such that the angle $OPA$ is a maximum.

CanadianMO-1977-2.jpg


Solution

Problem 3

$N$ is an integer whose representation in base $b$ is $777.$ Find the smallest positive integer $b$ for which $N$ is the fourth power of an integer.

Solution

Problem 4

Let \[p(x)=a_nx^n+a_{n-1}x^{n-1}+\cdots +a_1x+a_0\] and \[q(x)=b_mx^m+b_{m-1}x^{m-1}+\cdots +b_1x+b_0\] be two polynomials with integer coefficients. Suppose that all of the coefficients of the product $p(x)\cdot q(x)$ are even, but not all of them are divisible by 4. Show that one of $p(x)$ and $q(x)$ has all even coefficients and the other has at least one odd coefficient.


Solution

Problem 5

A right circular cone of base radius $1$ cm and slant height of $3$ cm is given. $P$ is a point on the circumference of the base and the shortest path from $P$ around the cone is drawn (see diagram). What is the minimum distance from the vertex $V$ to this path?

[asy] path p1=yscale(.25)*arc((0,0),1,0,180); path p2=yscale(.25)*arc((0,0),1,0,-180); path q1=shift(-.25,.4)*rotate(30)*xscale(.85)*p1; path q2=shift(-.25,.4)*rotate(30)*xscale(.85)*p2; draw(p2,black);draw(q2,black); draw(p1,dashed);draw(q1,dashed); draw((-1,0)--(-.5,2.4)--(1,0)); MP("P",(-1,0),W);MP("V",(-.5,2.4),N); draw((-.2,2.5)--(1.2,.2),arrow=ArcArrow()); draw((1.2,.2)--(-.2,2.5),arrow=ArcArrow()); draw((0,0)--(1,0),arrow=ArcArrow()); draw((1,0)--(0,0),arrow=ArcArrow()); MP("1 cm",(.5,.04),S);MP("3 cm",(.5,1.35),NE); [/asy]


Solution

Problem 6

Let $0<u<1$ and define \[u_1=1+u\quad ,\quad u_2=\frac{1}{u_1}+u\quad \ldots\quad u_{n+1}=\frac{1}{u_n}+u\quad ,\quad n\ge 1\] Show that $u_n>1$ for all values of $n=1,2,3\ldots$.

Solution

Problem 7

A rectangular city is exactly $m$ blocks long and $n$ blocks wide (see diagram). A woman lives on the southwest corner of the city and works in the northeast corner. She walks to work each day but, on any given trip, she makes sure that her path does not include any intersection twice. Show that the number $f(m,n)$ of different paths she can take to work satisfies $f(m,n)\le 2^{mn}$.

\[\underbrace{ \left. \begin{array}{|c|c|c|c|c|c|c|c|c|c|c| } \hline &&&&&&&&&& \\ \hline &&&&&&&&&& \\ \hline &&&&&&&&&& \\ \hline &&&&&&&&&& \\ \hline &&&&&&&&&& \\ \hline &&&&&&&&&& \\ \hline &&&&&&&&&& \\ \hline \end{array} \right\}n}_m\]

Solution

Resources

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=1977_Canadian_MO_Problems&oldid=68681"