Difference between revisions of "2019 AIME II Problems/Problem 11"

Latest revision as of 15:46, 12 June 2025

Problem

Triangle $ABC$ has side lengths $AB=7, BC=8,$ and $CA=9.$ Circle $\omega_1$ passes through $B$ and is tangent to line $AC$ at $A.$ Circle $\omega_2$ passes through $C$ and is tangent to line $AB$ at $A.$ Let $K$ be the intersection of circles $\omega_1$ and $\omega_2$ not equal to $A.$ Then $AK=\tfrac mn,$ where $m$ and $n$ are relatively prime positive integers. Find $m+n.$

Solution 1

$[asy] unitsize(20); pair B = (0,0); pair A = (2,sqrt(45)); pair C = (8,0); draw(circumcircle(A,B,(-17/8,0)),rgb(.7,.7,.7)); draw(circumcircle(A,C,(49/8,0)),rgb(.7,.7,.7)); draw(B--A--C--cycle); label("$A$",A,dir(105)); label("$B$",B,dir(-135)); label("$C$",C,dir(-75)); dot((2.68,2.25)); label("$K$",(2.68,2.25),2*down); label("$\omega_1$",(-4.5,1)); label("$\omega_2$",(12.75,6)); label("$7$",(A+B)/2,dir(140)); label("$8$",(B+C)/2,dir(-90)); label("$9$",(A+C)/2,dir(60)); [/asy]$ -Diagram by Brendanb4321

Note that from the tangency condition that the supplement of $\angle CAB$ with respects to lines $AB$ and $AC$ are equal to $\angle AKB$ and $\angle AKC$ , respectively, so from tangent-chord, $\angle AKC=\angle AKB=180^{\circ}-\angle BAC$ Also note that $\angle ABK=\angle KAC$ $^{(*)}$ , so $\triangle AKB\sim \triangle CKA$ . Using similarity ratios, we can easily find $AK^2=BK*KC$ However, since $AB=7$ and $CA=9$ , we can use similarity ratios to get $BK=\frac{7}{9}AK, CK=\frac{9}{7}AK$

Now we use Law of Cosines on $\triangle AKB$ : From reverse Law of Cosines, $\cos{\angle BAC}=\frac{11}{21}\implies \cos{(180^{\circ}-\angle BAC)}=\angle AKB=-\frac{11}{21}$

Giving us $AK^2+\frac{49}{81}AK^2+\frac{22}{27}AK^2=49$ $\implies \frac{196}{81}AK^2=49$ $AK=\frac{9}{2}$ so our answer is $9+2=\boxed{011}$ .

$^{(*)}$ Let $O$ be the center of $\omega_1$ . Then $\angle KAC = 90 - \angle OAK = 90 - \frac{1}{2}(180 - \angle AOK) = \frac{\angle AOK}{2} = \angle ABK$ . Thus, $\angle ABK = \angle KAC$

-franchester; $^{(*)}$ by firebolt360

Supplement

In order to get to the Law of Cosines first, we first apply the LOC to $\triangle{ABC},$ obtaining $\angle{BAC}.$
We angle chase before applying the law of cosines to $\angle{AKB}.$

Note that $\angle{ABK}=\angle{KAC}$ and $\angle{KCA}=\angle{KAB}$ from tangent-chord.

Thus, $\angle{AKC}=\angle{AKB}=180^{\circ}-(\angle{ABK}+\angle{KAB}).$

However from our tangent chord, note that: $\angle{ABK}+\angle{KAB}=\angle{KAC}+\angle{KAB}=\angle{BAC}.$ Thus, $\angle{AKB}=180^\circ-\angle{BAC}.$

As an alternative approach, note that the sum of the angles in quadrilateral $ABKC$ is $360^{\circ}$ and we can find $\angle{AKB}=\frac12$ of convex $\angle{BKC},$ which is just:

$\frac12 \left(360^{\circ}-2(\angle{KAB}+\angle{KBA}\right) = 180^\circ - \angle{BAC}.$

~mathboy282

Solution 2 (Inversion)

Consider an inversion with center $A$ and radius $r=AK$ . Then, we have $AB\cdot AB^*=AK^2$ , or $AB^*=\frac{AK^2}{7}$ . Similarly, $AC^*=\frac{AK^2}{9}$ . Notice that $AB^*KC^*$ is a parallelogram, since $\omega_1$ and $\omega_2$ are tangent to $AC$ and $AB$ , respectively. Thus, $AC^*=B^*K$ . Now, we get that $\cos(\angle AB^*K)=\cos(180-\angle BAC)=-\frac{11}{21}$ so by Law of Cosines on $\triangle AB^*K$ we have $(AK)^2=(AB^*)2+(B^*K)^2-2\cdot AB^*\cdot B^*K \cdot \cos(\angle AB^*K)$ $\Rightarrow (AK)^2=\frac{AK^4}{49}+\frac{AK^4}{81}-2\cdot \frac{AK^2}{7}\frac{AK^2}{9}\frac{-11}{21}$ $\Rightarrow 1=\frac{AK^2}{49}+\frac{AK^2}{81}+\frac{22AK^2}{63\cdot21}$ $\Rightarrow AK=\frac{9}{2}$ Then, our answer is $9+2=\boxed{11}$ . -brianzjk

Solution 3 (Death By Trig Bash)

Let the centers of the circles be $O_{1}$ and $O_{2}$ where the $O_{1}$ has the side length $7$ contained in the circle. Now let $\angle BAC =x.$ This implies $\angle O_{1}AB = \angle O_{1}BA = \angle O_{2}AC = \angle O_{2}CA = 90^{\circ}-x$ by the angle by by tangent. Then we also know that $\angle AO_{1}B = \angle AO_{2}C = 2x$ Now we first find $\cos x.$ We use law of cosines on $\bigtriangleup ABC$ to obtain $64 = 81 + 48 - 2 \cdot 9 \cdot 7 \cdot \cos{x}$ $\implies \cos{x} =\frac{11}{21}$ $\implies \sin{x} =\frac{8\sqrt{5}}{21}$ Then applying law of sines on $\bigtriangleup AO_{1}B$ we obtain $\frac{7}{\sin{2x}} =\frac{O_{1}B}{\sin{90^{\circ}-x}}$ $\implies\frac{7}{2\sin{x}\cos{x}} =\frac{O_{1}B}{\cos{x}}$ $\implies O_{1}B = O_{1}A=\frac{147}{16\sqrt{5}}$ Using similar logic we obtain $O_{2}A =\frac{189}{16\sqrt{5}}.$

Now we know that $\angle O_{1}AO_{2}=180^{\circ}-x.$ Thus using law of cosines on $\bigtriangleup O_{1}AO_{2}$ yields $O_{1}O_{2} =\sqrt{\left(\frac{147}{16\sqrt{5}}\right)^2+\left(\frac{189}{16\sqrt{5}}\right)^2-2\:\cdot \left(\frac{147}{16\sqrt{5}}\right)\cdot \frac{189}{16\sqrt{5}}\cdot -\frac{11}{21}}$ While this does look daunting we can write the above expression as $\sqrt{\left(\frac{189+147}{16\sqrt{5}}\right)^2 - 2\cdot \left(\frac{147}{16\sqrt{5}}\right)\cdot \frac{189}{16\sqrt{5}}\cdot \frac{10}{21}} =\sqrt{\left(\frac{168}{8\sqrt{5}}\right)^2 - \left(\frac{7 \cdot 189 \cdot 5}{8 \sqrt{5} \cdot 8\sqrt{5}}\right)}$ Then factoring yields $\sqrt{\frac{21^2(8^2-15)}{(8\sqrt{5})^2}} =\frac{147}{8\sqrt{5}}$ The area $[O_{1}AO_{2}] =\frac{1}{2} \cdot\frac{147}{16\sqrt{5}} \cdot\frac{189}{16\sqrt{5}} \cdot \sin(180^{\circ}-x) =\frac{1}{2} \cdot\frac{147}{16\sqrt{5}} \cdot\frac{189}{16\sqrt{5}} \cdot\frac{8\sqrt{5}}{21}$ Now $AK$ is twice the length of the altitude of $\bigtriangleup O_{1}AO_{2}$ so we let the altitude be $h$ and we have $\frac{1}{2} \cdot h \cdot\frac{147}{8\sqrt{5}} =\frac{1}{2} \cdot\frac{147}{16\sqrt{5}} \cdot\frac{189}{16\sqrt{5}} \cdot\frac{8\sqrt{5}}{21}$ $\implies h =\frac{9}{4}$ Thus our desired length is $\frac{9}{2} \implies m+n = \boxed{11}.$

-minor edits by faliure167

Solution 4 (Video)

Video Link: https://www.youtube.com/watch?v=nJydO5CLuuI

Solution 5 (Olympiad Geometry)

By the definition of $K$ , it is the spiral center mapping $BA\to AC$ , which means that it is the midpoint of the $A$ -symmedian chord. In particular, if $M$ is the midpoint of $BC$ and $M'$ is the reflection of $A$ across $K$ , we have $\triangle ABM'\sim\triangle AMC$ . By Stewart's Theorem, it then follows that $AK = \frac{AM'}{2} = \frac{AC\cdot AB}{2AM} = \frac{7\cdot 9}{2\sqrt{\frac{9^2\cdot 4 + 7^2\cdot 4 - 4^2\cdot 8}{8}}} = \frac{7\cdot 9}{2\sqrt{49}} = \frac{9}{2}\implies m + n = \boxed{11}.$

Solution 6 (Inversion simplified)

The median of $\triangle ABC$ is $AM = \sqrt{\frac {AB^2 + AC^2 }{2} – \frac{BC^2}{4}} = 7$ (via Stewart's Theorem).

Consider an inversion with center $A$ and radius $AK$ (inversion with respect the red circle). Let $K, B',$ and $C'$ be inverse points for $K, B,$ and $C,$ respectively.

Image of line $AB$ is line $AB, B'$ lies on this line.

Image of $\omega_2$ is line $KC'||AB$ (circle $\omega_2$ passes through K, C and is tangent to the line $AB$ at point $A.$ Diagram shows circle and its image using same color).

Similarly, $AC||B'K (B'K$ is the image of the circle $\omega_1$ ).

Therefore $AB'KC'$ is a parallelogram, $AF$ is median of $\triangle AB'C'$ and $AK = 2 AF.$ Then, we have $AB'=\frac{AK^2}{7}$ . $\triangle ABC \sim \triangle AC'B'$ with coefficient $k =\frac {AB'}{AC} = \frac{AK^2}{7\cdot 9}.$

So median $AF = k AM \implies \frac {AK}{2} = AM \cdot k = 7\cdot \frac{AK^2}{7\cdot 9} \implies AK = \frac{9}{2}.$ vladimir.shelomovskii@gmail.com, vvsss

Solution 7 (Heavy Bash)

We start by assigning coordinates to point $A$ , labeling it $(0,0)$ and point $B$ at $(7,0)$ , and letting point $C$ be above the $x$ -axis. Through an application of the Pythagorean Theorem and dropping an altitude to side $AB$ , it is easy to see that $C$ has coordinates $(33/7, 24\sqrt{5}/7)$ .

Let $O1$ be the center of circle $\omega_1$ and $O2$ be the center of circle $\omega_2$ . Since circle $\omega_1$ contains both points $A$ and $B$ , $O1$ must lie on the perpendicular bisector of line $AB$ , and similarly $O2$ must lie on the perpendicular bisector of line $AC$ . Through some calculations, we find that the perpendicular bisector of $AB$ has equation $x = 3.5$ , and the perpendicular bisector of $AC$ has equation $y = {-11\sqrt{5}/40 \cdot x} + 189\sqrt{5}/80$ .

Since circle $\omega_1$ is tangent to line $AC$ at $A$ , its radius must be perpendicular to $AC$ at $A$ . Therefore, the radius has equation $y = {{-11\cdot\sqrt{5}/40} \cdot x}$ . Substituting the $x$ -coordinate of $O1$ into this, we find the y-coordinate of $O1 = {{-11 \cdot \sqrt{5}/40} \cdot 7/2} = {-77 \cdot \sqrt{5}/80}$ .

Similarly, since circle $\omega_2$ is tangent to line $AB$ at $A$ , its radius must be perpendicular to $AB$ at $A$ . Therefore, the radius has equation $x = 0$ and combining with the previous result for $O2$ we get that the coordinates of $O2$ are $(0, 189\sqrt{5}/80)$ .

We now find the slope of $O1O2$ , the line joining the centers of circles $\omega_1$ and $\omega_2$ , which turns out to be ${({266 \cdot \sqrt{5} / 80}) \cdot -2/7} = {-19 \cdot \sqrt{5}/20}$ . Since the $y$ -intercept of that line is at $O2(0,189\sqrt{5}/80)$ , the equation is $y = {{-19 \cdot \sqrt{5}/20} \cdot x} + {189 \cdot \sqrt{5}/80}$ . Since circles $\omega_1$ and $\omega_2$ intersect at points $A$ and $K$ , line $AK$ is the radical axis of those circles, and since the radical axis is always perpendicular to the line joining the centers of the circles, $AK$ has slope ${4 \cdot \sqrt{5}/19}$ . Since point $A$ is $(0,0)$ , this line has a $y$ -intercept of $0$ , so it has equation $y$ = ${{4 \cdot \sqrt{5}/19} \cdot x}$ .

We set ${{4 \cdot \sqrt{5}/19} \cdot x} = {{-19 \cdot \sqrt{5}/20} \cdot x} + {189 \cdot \sqrt{5}/80}$ in order to find the intersection $I$ of the radical axis $AK$ and $O1O2$ . Through some moderate bashing, we find that the intersection point is $I(57/28, {3 \cdot \sqrt{5}/7})$ . We know that either intersection point of two circles is the same distance from the intersection of radical axis and line joining the centers of those circles, so reflecting $A$ over $I$ yields $K$ and $AK$ = $2AI$ = (This is the most tedious part of the bash) ${2 \cdot \sqrt{(57/28)^2 + ({3 \cdot \sqrt{5}/7)^2)}}} = {2 \cdot \sqrt{3969/784}} = {2 \cdot 63/28} = {2 \cdot 9/4} = 9/2$ . Therefore the answer is $9 + 2 = \boxed{011}.$

Solution 8 (Barybash)

We use barycentric coordinates with $A=(1,\,0,\,0)$ , $B=(0,\,1,\,0)$ , $C=(0,\,0,\,1)$ , $a:=BC$ , $b:=CA$ , $c:=AB$ . Suppose $\omega_1$ is given by $-a^2yz-b^2zx-c^2xy+wz=0$ . For $t\neq 0$ , the power of $D=(1-t,\,0,\,t)$ with respect to $\omega_1$ should always be positive since $D$ lies outside $\omega_1$ . Hence $-b^2t(1-t)+wt>0$ for all $t$ . It follows that $w=b^2$ . Similarly, $\omega_2$ is given by $-a^2yz-b^2zx-c^2xy+c^2y=0$ . Let $K=:(p,\,q,\,r)$ . Then $c^2q=b^2r$ so $r=\frac{c^2}{b^2}q$ and $p=1-q-\frac{c^2}{b^2}q$ . Plugging these into $\omega_2$ yields \begin{align*} -a^2&\left(\frac{c^2}{b^2}\right)q^2-b^2\left(\frac{c^2}{b^2}\right)q\left(1-q-\frac{c^2}{b^2}q\right)q-c^2q\left(1-q-\frac{c^2}{b^2}q\right)q+c^2q=0\\ \implies q&=\frac{b^2}{2b^2+2c^2-a^2}\\ \implies r&=\frac{c^2}{2b^2+2c^2-a^2}. \end{align*}Now $\overrightarrow{AK}=(-q-r,\,q,\,r)$ so \begin{align*} AK^2&=\left(\frac{1}{2b^2+2c^2-a^2}\right)^2(-a^2b^2c^2-b^2c^2(-b^2-c^2)-c^2b^2(-b^2-c^2))\\ &=\frac{b^2c^2}{2b^2+2c^2-a^2}\\ &=\frac{63^2}{196}. \end{align*}Thus $AK=\frac{9}{2}\implies\boxed{011}$ .

- KevinYang2.71

Solution 9 (for the memes)

We begin by trying to place $\triangle ABC$ in the coordinate plane. The semiperimeter is $\dfrac{7+8+9}{2}=12$ , so the area of $\triangle ABC$ is $\sqrt{12 \cdot 5 \cdot 4 \cdot 3}=12\sqrt{5}$ .

So, if we let $\overline{BC}$ be the base, then the height of the triangle must be $\frac{12 \sqrt 5}{\frac{1}{2} \cdot 8}=3 \sqrt{5}$ . Therefore, we can let $B=(0,0)$ , $C=(8,0)$ , and $A=(2, 3\sqrt5)$ .

Now, we can find the equations of $\omega_1$ and $\omega_2$ .

$\omega_1$ passes through $A$ and $B$ , so its center lies on the perpendicular bisector of $\overline{AB}$ . It is easy to determine that the equation of this perpendicular bisector is $y=\frac{-2\sqrt5}{15}x+\frac{49\sqrt5}{30}$ , so the coordinates of the center can be expressed as $\left(k, -\frac{2\sqrt5}{15}k+\frac{49\sqrt5}{30} \right)$ .

Since the distance from the center to $A$ must be equal to the distance from line $AC$ (which has equation $x\sqrt{5}+2y-8\sqrt{5}=0$ ), we can say that $k^2+\left(-\frac{2\sqrt5}{15} k+\frac{49\sqrt5}{30} \right)^2=\frac{1}{(\sqrt{5})^2+2^2} \left(k\sqrt{5}+2 \left(-\frac{2\sqrt5}{15}k+\frac{49\sqrt5}{30} \right)-8\sqrt5 \right)^2$ $k^2+\left(-\frac{2\sqrt{5}}{15}k+\frac{49\sqrt5}{30} \right)^2-\frac{1}{9} \left(\frac{11\sqrt5}{15}k-\frac{71\sqrt5}{15} \right)^2=0$ However, since we know that $\omega_1$ is tangent to $AC$ , this equation has only one solution. So, rather than solving the quadratic like one normally would, we can instead use Vieta's formulas.

It is easy to determine that the coefficient of $k^2$ in this equation is $\frac{64}{81}$ and that the coefficient of $k$ is $\frac{136}{81}$ . So, the sum of the solutions to this equation is $-\frac{136}{64}=-\frac{17}{8}$ . However, because these two solutions are the same, $k=-\frac{17}{16}$ and the center thus has coordinates $\left(-\frac{17}{16}, \frac{71\sqrt5}{40} \right)$ . From this, it is easy to determine that the equation of $\omega_1$ is $\left(x+\frac{17}{16} \right)^2+\left(y-\frac{71\sqrt{5}}{40} \right)^2=\frac{21609}{1280}$

We can determine the equation for $\omega_2$ in a similar manner. The perpendicular bisector of $\overline{AC}$ has equation $y=\frac{2\sqrt5}{5}x-\frac{\sqrt 5}{2}$ , so the center has coordinates of the form $\left(m, \frac{2\sqrt5}{5}m-\frac{\sqrt5}{2} \right)$ .

Again, the distance from the center to $C$ must be the same as the distance from the center to $AB$ (which has equation $3\sqrt{5}x-2y=0$ ). So, $(m-8)^2+\left(\frac{2\sqrt5}{5} m-\frac{\sqrt 5}{2} \right)^2=\frac{1}{(3\sqrt5)^2+2^2} \left(3\sqrt{5} m-2 \left(\frac{2\sqrt5}{5}m -\frac{\sqrt5}{2} \right) \right)^2$ $(m-8)^2+\left(\frac{2\sqrt5}{5} m-\frac{\sqrt 5}{2} \right)^2-\frac{1}{49} \left(\frac{11\sqrt5}{5}m+\sqrt 5 \right)^2=0$

Once again, the coefficient of $m^2$ in this equation is $\frac{64}{49}$ and the coefficient of $m$ is $-\frac{904}{49}$ . So, the value of $m$ is $-\frac{1}{2} \cdot \frac{-904}{64}=\frac{113}{16}$ and the coordinatees of the center of $\omega_2$ are thus $\left(\frac{113}{16}, \frac{93\sqrt5}{40} \right)$ . It follows that the equation of $\omega_2$ is $\left(x-\frac{113}{16} \right)^2+\left(y-\frac{93\sqrt5}{40} \right)^2=\frac{35721}{1280}$

Now, to find the coordinates of the intersection point $K$ , we begin by finding the line that the two intersection points lie on.

Subtracting the equations of the two circles and using the difference of squares factorization yields $(2x-6) \left(\frac{65}{8} \right)+\left(2y-\frac{41\sqrt5}{10} \right) \left(\frac{11\sqrt5}{20} \right)=-\frac{441}{40}$ $y=-\frac{65\sqrt5}{22}x+\frac{98\sqrt5}{11}$

Substituting this back into the equation of $\omega_1$ yields $\left(x+\frac{17}{16} \right)^2+\left(\frac{65\sqrt5}{22}x-\frac{3139\sqrt5}{440} \right)^2-\frac{21609}{1280}=0$

Now, we can use Vieta's formulas again rather than solving the quadratic. Since these circles intersect at $A$ , one of the solutions to the equation is $x=2$ . So, we can subtract $2$ from the sum of the solutions to obtain the $x$ -coordinate of $K$ .

The coefficient of $x^2$ in this equation is $\frac{21609}{484}$ and the coefficient of $x$ in this equation is $\frac{-100989}{484}$ . So, the sum of the solutions to the equation is $\frac{100989}{21609}=\frac{229}{49}$ and the $x$ -coordinate of $K$ is thus $\frac{229}{49}-2=\frac{131}{49}$ . It is easy to determine that the $y$ -coordinate of $K$ is $\frac{99\sqrt5}{98}$ .

To conclude, the length $AK$ is $\sqrt{\left(\frac{33}{49} \right)^2+\left(\frac{195 \sqrt 5}{98} \right)^2}=\frac{3}{98} \sqrt{21609}=\frac{9}{2}$ The requested sum is $m+n=9+2=\boxed{011}$ .

Solution 10 (Dumpty Point)

We recognize by the configuration that point $K$ is the A-dumpty point of $\triangle ABC$ , and is thus the midpoint of the chord formed by the A-symmedian. Consider the point where the A-symmedian intersects the circumcircle of $\triangle ABC$ , which we can denote as point $E$ . Then, we know that $K$ is the midpoint of $AE$ . Furthermore, draw the midpoint of $BC$ , which we can denote as point $M$ .

We note that $AM$ and $AE$ are the median and the symmedian, respectively, meaning that $AM$ and $AE$ are isogonal. In other words, we have $\angle BAM = \angle CAE$ . Furthermore, we have $\angle ABM = \angle AEC$ , meaning that $\triangle ABM \sim \triangle AEC$ .

Thus, we have $\frac{AE}{AB} = \frac{AC}{AM}$ , so $AE = \frac{(AB)(AC)}{AM} = \frac{63}{AM}$ . Since $K$ is the midpoint of $AE$ , we have $AK = \frac{63}{2(AM)}$ . Thus, it suffices to find the length of $AM$ .

By Stewart's Theorem, we have $4(4)(8)+8(AM)^2 = 4(7)^2+4(9)^2.$ Dividing by $4$ , we have $32+2(AM)^2 = 130,$ so $2(AM)^2 = 98$ and $AM = 7.$ Substituting back into the expression $AK = \frac{63}{2(AM)}$ , we get our final length of $AK = \boxed{\frac{9}{2}}$ which gives us the final answer $9+2 = \boxed{011}$ . We are done.

-cweu001

@@ Line 15: / Line 15: @@
 label("$C$",C,dir(-75));
 dot((2.68,2.25));
-label("$K$",(2.68,2.25),dir(-150));
+label("$K$",(2.68,2.25),2*down);
-label("$\omega_1$",(-6,1));
+label("$\omega_1$",(-4.5,1));
-label("$\omega_2$",(14,6));
+label("$\omega_2$",(12.75,6));
 label("$7$",(A+B)/2,dir(140));
 label("$8$",(B+C)/2,dir(-90));
@@ Line 25: / Line 25: @@
-Note that from the tangency condition that the supplement of <math>\angle CAB</math> with respects to lines <math>AB</math> and <math>AC</math> are equal to <math>\angle AKB</math> and <math>\angle AKC</math>, respectively, so from tangent-chord, <cmath>\angle AKC=\angle AKB=180^{\circ}-\angle BAC</cmath> Also note that <math>\angle ABK=\angle KAC</math>, so <math>\triangle AKB\sim \triangle CKA</math>. Using similarity ratios, we can easily find <cmath>AK^2=BK*KC</cmath> However, since <math>AB=7</math> and <math>CA=9</math>, we can use similarity ratios to get <cmath>BK=\frac{7}{9}AK, CK=\frac{9}{7}AK</cmath> Now we use Law of Cosines on <math>\triangle AKB</math>: From reverse Law of Cosines, <math>\cos{\angle BAC}=\frac{11}{21}\implies \cos{(180^{\circ}-\angle BAC)}=-\frac{11}{21}</math>. This gives us <cmath>AK^2+\frac{49}{81}AK^2+\frac{22}{27}AK^2=49</cmath> <cmath>\implies \frac{196}{81}AK^2=49</cmath> <cmath>AK=\frac{9}{2}</cmath> so our answer is <math>9+2=\boxed{011}</math>.
+Note that from the tangency condition that the supplement of <math>\angle CAB</math> with respects to lines <math>AB</math> and <math>AC</math> are equal to <math>\angle AKB</math> and <math>\angle AKC</math>, respectively, so from tangent-chord, <cmath>\angle AKC=\angle AKB=180^{\circ}-\angle BAC</cmath> Also note that <math>\angle ABK=\angle KAC</math><math>^{(*)}</math>, so <math>\triangle AKB\sim \triangle CKA</math>. Using similarity ratios, we can easily find <cmath>AK^2=BK*KC</cmath> However, since <math>AB=7</math> and <math>CA=9</math>, we can use similarity ratios to get <cmath>BK=\frac{7}{9}AK, CK=\frac{9}{7}AK</cmath>
--franchester
+*Now we use Law of Cosines on <math>\triangle AKB</math>: From reverse Law of Cosines, <math>\cos{\angle BAC}=\frac{11}{21}\implies \cos{(180^{\circ}-\angle BAC)}=\angle AKB=-\frac{11}{21}</math>
+Giving us <cmath>AK^2+\frac{49}{81}AK^2+\frac{22}{27}AK^2=49</cmath> <cmath>\implies \frac{196}{81}AK^2=49</cmath> <cmath>AK=\frac{9}{2}</cmath> so our answer is <math>9+2=\boxed{011}</math>.
+<math>^{(*)}</math> Let <math>O</math> be the center of <math>\omega_1</math>. Then <math>\angle KAC = 90 - \angle OAK = 90 - \frac{1}{2}(180 - \angle AOK) = \frac{\angle AOK}{2} = \angle ABK</math>. Thus, <math>\angle ABK = \angle KAC</math>
+-franchester; <math>^{(*)}</math> by firebolt360
+===Supplement===
+*In order to get to the Law of Cosines first, we first apply the LOC to <math>\triangle{ABC},</math> obtaining <math>\angle{BAC}.</math>
+*We angle chase before applying the law of cosines to <math>\angle{AKB}.</math>
+Note that <math>\angle{ABK}=\angle{KAC}</math> and <math>\angle{KCA}=\angle{KAB}</math> from tangent-chord.
+Thus, <math>\angle{AKC}=\angle{AKB}=180^{\circ}-(\angle{ABK}+\angle{KAB}).</math>
+However from our tangent chord, note that:
+<cmath>\angle{ABK}+\angle{KAB}=\angle{KAC}+\angle{KAB}=\angle{BAC}.</cmath>
+Thus, <math>\angle{AKB}=180^\circ-\angle{BAC}.</math>
+*As an alternative approach, note that the sum of the angles in quadrilateral <math>ABKC</math> is <math>360^{\circ}</math> and we can find <math>\angle{AKB}=\frac12</math> of convex <math>\angle{BKC},</math> which is just:
+<cmath>\frac12 \left(360^{\circ}-2(\angle{KAB}+\angle{KBA}\right) = 180^\circ - \angle{BAC}.</cmath>
+~mathboy282
 ==Solution 2 (Inversion)==
 Consider an inversion with center <math>A</math> and radius <math>r=AK</math>. Then, we have <math>AB\cdot AB^*=AK^2</math>, or <math>AB^*=\frac{AK^2}{7}</math>. Similarly, <math>AC^*=\frac{AK^2}{9}</math>. Notice that <math>AB^*KC^*</math> is a parallelogram, since <math>\omega_1</math> and <math>\omega_2</math> are tangent to <math>AC</math> and <math>AB</math>, respectively. Thus, <math>AC^*=B^*K</math>. Now, we get that
-<cmath>\cos(\angle AB^*K)=-\cos(180-\angle BAC)=-\frac{11}{21}</cmath>
+<cmath>\cos(\angle AB^*K)=\cos(180-\angle BAC)=-\frac{11}{21}</cmath>
 so by Law of Cosines on <math>\triangle AB^*K</math> we have
 <cmath>(AK)^2=(AB^*)2+(B^*K)^2-2\cdot AB^*\cdot B^*K \cdot \cos(\angle AB^*K)</cmath>
 <cmath>\Rightarrow (AK)^2=\frac{AK^4}{49}+\frac{AK^4}{81}-2\cdot \frac{AK^2}{7}\frac{AK^2}{9}\frac{-11}{21}</cmath>
-<cmath>\Rightarrow 1=\frac{AK^2}{49}+\frac{AK^2}{81}+\frac{11AK^2}{63\cdot21}</cmath>
+<cmath>\Rightarrow 1=\frac{AK^2}{49}+\frac{AK^2}{81}+\frac{22AK^2}{63\cdot21}</cmath>
 <cmath>\Rightarrow AK=\frac{9}{2}</cmath>
 Then, our answer is <math>9+2=\boxed{11}</math>.
 -brianzjk
-==Solution 3 (Video)==
+== Solution 3 (Death By Trig Bash) ==
+Let the centers of the circles be <math>O_{1}</math> and <math>O_{2}</math> where the <math>O_{1}</math> has the side length <math>7</math> contained in the circle. Now let <math>\angle BAC =x.</math> This implies <cmath>\angle O_{1}AB = \angle O_{1}BA = \angle O_{2}AC = \angle O_{2}CA = 90^{\circ}-x</cmath> by the angle by by tangent. Then we also know that <cmath>\angle AO_{1}B = \angle AO_{2}C = 2x</cmath> Now we first find <math>\cos x.</math> We use law of cosines on <math>\bigtriangleup ABC</math> to obtain <cmath>64 = 81 + 48 - 2 \cdot 9 \cdot 7 \cdot \cos{x}</cmath> <cmath>\implies \cos{x} =\frac{11}{21}</cmath> <cmath>\implies \sin{x} =\frac{8\sqrt{5}}{21}</cmath> Then applying law of sines on <math>\bigtriangleup AO_{1}B</math> we obtain <cmath>\frac{7}{\sin{2x}} =\frac{O_{1}B}{\sin{90^{\circ}-x}}</cmath> <cmath>\implies\frac{7}{2\sin{x}\cos{x}} =\frac{O_{1}B}{\cos{x}}</cmath> <cmath>\implies O_{1}B = O_{1}A=\frac{147}{16\sqrt{5}}</cmath> Using similar logic we obtain <math>O_{2}A =\frac{189}{16\sqrt{5}}.</math>
+Now we know that <math>\angle O_{1}AO_{2}=180^{\circ}-x.</math> Thus using law of cosines on <math>\bigtriangleup O_{1}AO_{2}</math> yields <cmath>O_{1}O_{2} =\sqrt{\left(\frac{147}{16\sqrt{5}}\right)^2+\left(\frac{189}{16\sqrt{5}}\right)^2-2\:\cdot \left(\frac{147}{16\sqrt{5}}\right)\cdot \frac{189}{16\sqrt{5}}\cdot -\frac{11}{21}}</cmath> While this does look daunting we can write the above expression as <cmath>\sqrt{\left(\frac{189+147}{16\sqrt{5}}\right)^2 - 2\cdot \left(\frac{147}{16\sqrt{5}}\right)\cdot \frac{189}{16\sqrt{5}}\cdot \frac{10}{21}} =\sqrt{\left(\frac{168}{8\sqrt{5}}\right)^2 - \left(\frac{7 \cdot 189 \cdot 5}{8 \sqrt{5} \cdot 8\sqrt{5}}\right)}</cmath> Then factoring yields <cmath>\sqrt{\frac{21^2(8^2-15)}{(8\sqrt{5})^2}} =\frac{147}{8\sqrt{5}}</cmath> The area <cmath>[O_{1}AO_{2}] =\frac{1}{2} \cdot\frac{147}{16\sqrt{5}} \cdot\frac{189}{16\sqrt{5}} \cdot \sin(180^{\circ}-x) =\frac{1}{2} \cdot\frac{147}{16\sqrt{5}} \cdot\frac{189}{16\sqrt{5}} \cdot\frac{8\sqrt{5}}{21}</cmath> Now <math>AK</math> is twice the length of the altitude of <math>\bigtriangleup O_{1}AO_{2}</math> so we let the altitude be <math>h</math> and we have <cmath>\frac{1}{2} \cdot h \cdot\frac{147}{8\sqrt{5}} =\frac{1}{2} \cdot\frac{147}{16\sqrt{5}} \cdot\frac{189}{16\sqrt{5}} \cdot\frac{8\sqrt{5}}{21}</cmath> <cmath>\implies h =\frac{9}{4}</cmath> Thus our desired length is <math>\frac{9}{2} \implies m+n = \boxed{11}.</math>
+-minor edits by faliure167
+==Solution 4 (Video)==
 Video Link: https://www.youtube.com/watch?v=nJydO5CLuuI
+==Solution 5 (Olympiad Geometry)==
+By the definition of <math>K</math>, it is the spiral center mapping <math>BA\to AC</math>, which means that it is the midpoint of the <math>A</math>-symmedian chord. In particular, if <math>M</math> is the midpoint of <math>BC</math> and <math>M'</math> is the reflection of <math>A</math> across <math>K</math>, we have <math>\triangle ABM'\sim\triangle AMC</math>. By Stewart's Theorem, it then follows that
+<cmath>AK = \frac{AM'}{2} = \frac{AC\cdot AB}{2AM} = \frac{7\cdot 9}{2\sqrt{\frac{9^2\cdot 4 + 7^2\cdot 4 - 4^2\cdot 8}{8}}} = \frac{7\cdot 9}{2\sqrt{49}} = \frac{9}{2}\implies m + n = \boxed{11}.</cmath>
+==Solution 6 (Inversion simplified)==
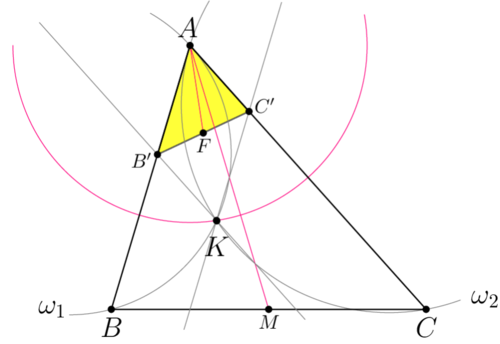
+[[File:AIME-II-2019-11.png|500px|right]]
+The median of <math>\triangle ABC</math> is <math>AM = \sqrt{\frac {AB^2 +  AC^2 }{2} – \frac{BC^2}{4}} = 7</math> (via Stewart's Theorem).
+Consider an inversion with center <math>A</math> and radius <math>AK</math> (inversion with respect the red circle).
+Let <math>K, B',</math> and <math>C'</math> be inverse points for <math>K, B,</math> and <math>C,</math> respectively.
+Image of line <math>AB</math> is line <math>AB, B'</math> lies on this line.
+Image of <math>\omega_2</math> is line <math>KC'||AB</math> (circle <math>\omega_2</math> passes through K, C and is tangent to the line <math>AB</math> at point <math>A.</math> Diagram shows circle and its image using same color).
+Similarly, <math>AC||B'K (B'K</math> is the image of the circle <math>\omega_1</math>).
+Therefore <math>AB'KC'</math> is a parallelogram, <math>AF</math> is median of <math>\triangle AB'C'</math> and <math>AK = 2 AF.</math>
+Then, we have <math>AB'=\frac{AK^2}{7}</math>.  <math>\triangle ABC \sim \triangle AC'B'</math> with coefficient <math>k =\frac {AB'}{AC} = \frac{AK^2}{7\cdot 9}.</math>
+So median <cmath>AF = k AM \implies \frac {AK}{2} = AM \cdot k = 7\cdot  \frac{AK^2}{7\cdot 9} \implies  AK = \frac{9}{2}.</cmath>
+'''vladimir.shelomovskii@gmail.com, vvsss'''
+== Solution 7 (Heavy Bash) ==
+We start by assigning coordinates to point <math>A</math>, labeling it <math>(0,0)</math> and point <math>B</math> at <math>(7,0)</math>, and letting point <math>C</math> be above the <math>x</math>-axis. Through an application of the Pythagorean Theorem and dropping an altitude to side <math>AB</math>, it is easy to see that <math>C</math> has coordinates <math>(33/7, 24\sqrt{5}/7)</math>.
+Let <math>O1</math> be the center of circle <math>\omega_1</math>  and <math>O2</math> be the center of circle <math>\omega_2</math>. Since circle <math>\omega_1</math> contains both points <math>A</math> and <math>B</math>, <math>O1</math> must lie on the perpendicular bisector of line <math>AB</math>, and similarly <math>O2</math> must lie on the perpendicular bisector of line <math>AC</math>. Through some calculations, we find that the perpendicular bisector of <math>AB</math> has equation <math>x = 3.5</math>, and the perpendicular bisector of <math>AC</math> has equation <math>y = {-11\sqrt{5}/40 \cdot x} + 189\sqrt{5}/80</math>.
+Since circle <math>\omega_1</math> is tangent to line <math>AC</math> at <math>A</math>, its radius must be perpendicular to <math>AC</math> at <math>A</math>.
+Therefore, the radius has equation <math>y = {{-11\cdot\sqrt{5}/40} \cdot x}</math>. Substituting the <math>x</math>-coordinate of <math>O1</math> into this, we find the y-coordinate of <math>O1 = {{-11 \cdot \sqrt{5}/40} \cdot 7/2} = {-77 \cdot \sqrt{5}/80}</math>.
+Similarly, since circle <math>\omega_2</math> is tangent to line <math>AB</math> at <math>A</math>, its radius must be perpendicular to <math>AB</math> at <math>A</math>. Therefore, the radius has equation <math>x = 0</math> and combining with the previous result for <math>O2</math> we get that the coordinates of <math>O2</math> are <math>(0, 189\sqrt{5}/80)</math>.
+We now find the slope of <math>O1O2</math>, the line joining the centers of circles <math>\omega_1</math> and <math>\omega_2</math>, which turns out to be <math>{({266 \cdot \sqrt{5} / 80}) \cdot -2/7} = {-19 \cdot \sqrt{5}/20}</math>. Since the <math>y</math>-intercept of that line is at <math>O2(0,189\sqrt{5}/80)</math>, the equation is <math>y = {{-19 \cdot \sqrt{5}/20} \cdot x} + {189 \cdot \sqrt{5}/80}</math>.  Since circles <math>\omega_1</math> and <math>\omega_2</math> intersect at points <math>A</math> and <math>K</math>, line <math>AK</math> is the radical axis of those circles, and since the radical axis is always perpendicular to the line joining the centers of the circles, <math>AK</math> has slope <math>{4 \cdot \sqrt{5}/19}</math>. Since point <math>A</math> is <math>(0,0)</math>, this line has a <math>y</math>-intercept of <math>0</math>, so it has equation <math>y</math> = <math>{{4 \cdot \sqrt{5}/19} \cdot x}</math>.
+We set <math>{{4 \cdot \sqrt{5}/19} \cdot x} = {{-19 \cdot \sqrt{5}/20} \cdot x} + {189 \cdot \sqrt{5}/80}</math> in order to find the intersection <math>I</math> of the radical axis <math>AK</math> and <math>O1O2</math>. Through some moderate bashing, we find that the intersection point is <math>I(57/28, {3 \cdot \sqrt{5}/7})</math>. We know that either intersection point of two circles is the same distance from the intersection of radical axis and line joining the centers of those circles, so reflecting <math>A</math> over <math>I</math> yields <math>K</math> and <math>AK</math> = <math>2AI</math> = (This is the most tedious part of the bash) <math>{2 \cdot \sqrt{(57/28)^2 + ({3 \cdot \sqrt{5}/7)^2)}}} = {2 \cdot \sqrt{3969/784}} = {2 \cdot 63/28} = {2 \cdot 9/4} = 9/2</math>. Therefore the answer is <math>9 + 2 = \boxed{011}.</math>
+== Solution 8 (Barybash) ==
+We use barycentric coordinates with <math>A=(1,\,0,\,0)</math>, <math>B=(0,\,1,\,0)</math>, <math>C=(0,\,0,\,1)</math>, <math>a:=BC</math>, <math>b:=CA</math>, <math>c:=AB</math>. Suppose <math>\omega_1</math> is given by <math>-a^2yz-b^2zx-c^2xy+wz=0</math>. For <math>t\neq 0</math>, the power of <math>D=(1-t,\,0,\,t)</math> with respect to <math>\omega_1</math> should always be positive since <math>D</math> lies outside <math>\omega_1</math>. Hence <math>-b^2t(1-t)+wt>0</math> for all <math>t</math>. It follows that <math>w=b^2</math>. Similarly, <math>\omega_2</math> is given by <math>-a^2yz-b^2zx-c^2xy+c^2y=0</math>. Let <math>K=:(p,\,q,\,r)</math>. Then <math>c^2q=b^2r</math> so <math>r=\frac{c^2}{b^2}q</math> and <math>p=1-q-\frac{c^2}{b^2}q</math>. Plugging these into <math>\omega_2</math> yields
+\begin{align*}
+-a^2&\left(\frac{c^2}{b^2}\right)q^2-b^2\left(\frac{c^2}{b^2}\right)q\left(1-q-\frac{c^2}{b^2}q\right)q-c^2q\left(1-q-\frac{c^2}{b^2}q\right)q+c^2q=0\\
+\implies q&=\frac{b^2}{2b^2+2c^2-a^2}\\
+\implies r&=\frac{c^2}{2b^2+2c^2-a^2}.
+\end{align*}Now <math>\overrightarrow{AK}=(-q-r,\,q,\,r)</math> so
+\begin{align*}
+AK^2&=\left(\frac{1}{2b^2+2c^2-a^2}\right)^2(-a^2b^2c^2-b^2c^2(-b^2-c^2)-c^2b^2(-b^2-c^2))\\
+&=\frac{b^2c^2}{2b^2+2c^2-a^2}\\
+&=\frac{63^2}{196}.
+\end{align*}Thus <math>AK=\frac{9}{2}\implies\boxed{011}</math>.
+- KevinYang2.71
+== Solution 9 (for the memes) ==
+We begin by trying to place <math>\triangle ABC</math> in the coordinate plane. The semiperimeter is <math>\dfrac{7+8+9}{2}=12</math>, so the area of <math>\triangle ABC</math> is <math>\sqrt{12 \cdot 5 \cdot 4 \cdot 3}=12\sqrt{5}</math>.
+So, if we let <math>\overline{BC}</math> be the base, then the height of the triangle must be <math>\frac{12 \sqrt 5}{\frac{1}{2} \cdot 8}=3 \sqrt{5}</math>. Therefore, we can let <math>B=(0,0)</math>, <math>C=(8,0)</math>, and <math>A=(2, 3\sqrt5)</math>.
+Now, we can find the equations of <math>\omega_1</math> and <math>\omega_2</math>.
+<math>\omega_1</math> passes through <math>A</math> and <math>B</math>, so its center lies on the perpendicular bisector of <math>\overline{AB}</math>. It is easy to determine that the equation of this perpendicular bisector is <math>y=\frac{-2\sqrt5}{15}x+\frac{49\sqrt5}{30}</math>, so the coordinates of the center can be expressed as <math>\left(k, -\frac{2\sqrt5}{15}k+\frac{49\sqrt5}{30} \right)</math>.
+Since the distance from the center to <math>A</math> must be equal to the distance from line <math>AC</math> (which has equation <math>x\sqrt{5}+2y-8\sqrt{5}=0</math>), we can say that
+<cmath>k^2+\left(-\frac{2\sqrt5}{15} k+\frac{49\sqrt5}{30} \right)^2=\frac{1}{(\sqrt{5})^2+2^2} \left(k\sqrt{5}+2 \left(-\frac{2\sqrt5}{15}k+\frac{49\sqrt5}{30} \right)-8\sqrt5 \right)^2</cmath> <cmath>k^2+\left(-\frac{2\sqrt{5}}{15}k+\frac{49\sqrt5}{30} \right)^2-\frac{1}{9} \left(\frac{11\sqrt5}{15}k-\frac{71\sqrt5}{15} \right)^2=0</cmath>
+However, since we know that <math>\omega_1</math> is tangent to <math>AC</math>, this equation has only one solution. So, rather than solving the quadratic like one normally would, we can instead use Vieta's formulas.
+It is easy to determine that the coefficient of <math>k^2</math> in this equation is <math>\frac{64}{81}</math> and that the coefficient of <math>k</math> is <math>\frac{136}{81}</math>. So, the sum of the solutions to this equation is <math>-\frac{136}{64}=-\frac{17}{8}</math>. However, because these two solutions are the same, <math>k=-\frac{17}{16}</math> and the center thus has coordinates <math>\left(-\frac{17}{16}, \frac{71\sqrt5}{40} \right)</math>. From this, it is easy to determine that the equation of <math>\omega_1</math> is <cmath>\left(x+\frac{17}{16} \right)^2+\left(y-\frac{71\sqrt{5}}{40} \right)^2=\frac{21609}{1280}</cmath>
+We can determine the equation for <math>\omega_2</math> in a similar manner. The perpendicular bisector of <math>\overline{AC}</math> has equation <math>y=\frac{2\sqrt5}{5}x-\frac{\sqrt 5}{2}</math>, so the center has coordinates of the form <math>\left(m, \frac{2\sqrt5}{5}m-\frac{\sqrt5}{2} \right)</math>.
+Again, the distance from the center to <math>C</math> must be the same as the distance from the center to <math>AB</math> (which has equation <math>3\sqrt{5}x-2y=0</math>). So, <cmath>(m-8)^2+\left(\frac{2\sqrt5}{5} m-\frac{\sqrt 5}{2} \right)^2=\frac{1}{(3\sqrt5)^2+2^2} \left(3\sqrt{5} m-2 \left(\frac{2\sqrt5}{5}m -\frac{\sqrt5}{2} \right) \right)^2</cmath> <cmath>(m-8)^2+\left(\frac{2\sqrt5}{5} m-\frac{\sqrt 5}{2} \right)^2-\frac{1}{49} \left(\frac{11\sqrt5}{5}m+\sqrt 5 \right)^2=0</cmath>
+Once again, the coefficient of <math>m^2</math> in this equation is <math>\frac{64}{49}</math> and the coefficient of <math>m</math> is <math>-\frac{904}{49}</math>. So, the value of <math>m</math> is <math>-\frac{1}{2} \cdot \frac{-904}{64}=\frac{113}{16}</math> and the coordinatees of the center of <math>\omega_2</math> are thus <math>\left(\frac{113}{16}, \frac{93\sqrt5}{40} \right)</math>. It follows that the equation of <math>\omega_2</math> is <cmath>\left(x-\frac{113}{16} \right)^2+\left(y-\frac{93\sqrt5}{40} \right)^2=\frac{35721}{1280}</cmath>
+Now, to find the coordinates of the intersection point <math>K</math>, we begin by finding the line that the two intersection points lie on.
+Subtracting the equations of the two circles and using the difference of squares factorization yields <cmath>(2x-6) \left(\frac{65}{8} \right)+\left(2y-\frac{41\sqrt5}{10} \right) \left(\frac{11\sqrt5}{20} \right)=-\frac{441}{40}</cmath> <cmath>y=-\frac{65\sqrt5}{22}x+\frac{98\sqrt5}{11}</cmath>
+Substituting this back into the equation of <math>\omega_1</math> yields <cmath>\left(x+\frac{17}{16} \right)^2+\left(\frac{65\sqrt5}{22}x-\frac{3139\sqrt5}{440} \right)^2-\frac{21609}{1280}=0</cmath>
+Now, we can use Vieta's formulas again rather than solving the quadratic. Since these circles intersect at <math>A</math>, one of the solutions to the equation is <math>x=2</math>. So, we can subtract <math>2</math> from the sum of the solutions to obtain the <math>x</math>-coordinate of <math>K</math>.
+The coefficient of <math>x^2</math> in this equation is <math>\frac{21609}{484}</math> and the coefficient of <math>x</math> in this equation is <math>\frac{-100989}{484}</math>. So, the sum of the solutions to the equation is <math>\frac{100989}{21609}=\frac{229}{49}</math> and the <math>x</math>-coordinate of <math>K</math> is thus <math>\frac{229}{49}-2=\frac{131}{49}</math>. It is easy to determine that the <math>y</math>-coordinate of <math>K</math> is <math>\frac{99\sqrt5}{98}</math>.
+To conclude, the length <math>AK</math> is <cmath>\sqrt{\left(\frac{33}{49} \right)^2+\left(\frac{195 \sqrt 5}{98} \right)^2}=\frac{3}{98} \sqrt{21609}=\frac{9}{2}</cmath> The requested sum is <math>m+n=9+2=\boxed{011}</math>.
+== Solution 10 (Dumpty Point) ==
+We recognize by the configuration that point <math>K</math> is the A-dumpty point of <math>\triangle ABC</math>, and is thus the midpoint of the chord formed by the A-symmedian. Consider the point where the A-symmedian intersects the circumcircle of <math>\triangle ABC</math>, which we can denote as point <math>E</math>. Then, we know that <math>K</math> is the midpoint of <math>AE</math>. Furthermore, draw the midpoint of <math>BC</math>, which we can denote as point <math>M</math>.
+We note that <math>AM</math> and <math>AE</math> are the median and the symmedian, respectively, meaning that <math>AM</math> and <math>AE</math> are isogonal. In other words, we have <math>\angle BAM = \angle CAE</math>. Furthermore, we have <math>\angle ABM = \angle AEC</math>, meaning that <math>\triangle ABM \sim \triangle AEC</math>.
+Thus, we have <math>\frac{AE}{AB} = \frac{AC}{AM}</math>, so <math>AE = \frac{(AB)(AC)}{AM} = \frac{63}{AM}</math>. Since <math>K</math> is the midpoint of <math>AE</math>, we have <math>AK = \frac{63}{2(AM)}</math>. Thus, it suffices to find the length of <math>AM</math>.
+By Stewart's Theorem, we have <cmath>4(4)(8)+8(AM)^2 = 4(7)^2+4(9)^2.</cmath> Dividing by <math>4</math>, we have <math>32+2(AM)^2 = 130,</math> so <math>2(AM)^2 = 98</math> and <cmath>AM = 7.</cmath> Substituting back into the expression <math>AK = \frac{63}{2(AM)}</math>, we get our final length of <math>AK = \boxed{\frac{9}{2}}</math> which gives us the final answer <math>9+2 = \boxed{011}</math>. We are done.
+-cweu001
 ==See Also==
 {{AIME box|year=2019|n=II|num-b=10|num-a=12}}
+[[Category: Intermediate Geometry Problems]]
 {{MAA Notice}}

2019 AIME II (Problems • Answer Key • Resources)
Preceded by Problem 10	Followed by Problem 12
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

Page

Toolbox

Search