Difference between revisions of "2021 April MIMC 10 Problems/Problem 22"
Cellsecret (talk | contribs) (→Solution) |
Cellsecret (talk | contribs) (→Solution) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 12: | Line 12: | ||
We can set <math>FG=x</math>, so <math>IF=3-\sqrt{2}-x</math>. Using the similar triangle, <math>\frac{GE}{AI}=\frac{FG}{IF}</math>. Plugging the numbers into the ratio, we can get <math>\frac{3-\sqrt{2}}{2\sqrt{2}-1}=\frac{x}{3-\sqrt{2}-x}</math>. | We can set <math>FG=x</math>, so <math>IF=3-\sqrt{2}-x</math>. Using the similar triangle, <math>\frac{GE}{AI}=\frac{FG}{IF}</math>. Plugging the numbers into the ratio, we can get <math>\frac{3-\sqrt{2}}{2\sqrt{2}-1}=\frac{x}{3-\sqrt{2}-x}</math>. | ||
| − | <math> | + | <math>~~~~~~~~~~~~~~~~~~~~\frac{3-\sqrt{2}}{2\sqrt{2}-1}=\frac{x}{3-\sqrt{2}-x}</math> |
<math>~(3-\sqrt{2})(3-\sqrt{2}-x)=x(2\sqrt{2}-1)</math> | <math>~(3-\sqrt{2})(3-\sqrt{2}-x)=x(2\sqrt{2}-1)</math> | ||
| Line 25: | Line 25: | ||
Solve for <math>HG</math>: | Solve for <math>HG</math>: | ||
| − | Since angle <math>HEC</math> is <math>90\ | + | Since angle <math>HEC</math> is <math>90^\circ</math> and angle <math>HCE</math> is <math>45^\circ</math>, <math>EC=HE=2\sqrt{2}-1</math>. Since <math>GE=3-\sqrt{2}</math>, <math>HG=2\sqrt{2}-1-(3-\sqrt{2})=3\sqrt{2}-4</math>. |
Finally, we can solve for <math>FH^2</math>, that is, <math>FG^2+HG^2=(\frac{34-23\sqrt{2}}{2})^2+(3\sqrt{2}-4)^2=\frac{1175-830\sqrt{2}}{2}</math>. Therefore, our answer would be <math>1175-830+2+2=\fbox{\textbf{(D)} 349}</math>. | Finally, we can solve for <math>FH^2</math>, that is, <math>FG^2+HG^2=(\frac{34-23\sqrt{2}}{2})^2+(3\sqrt{2}-4)^2=\frac{1175-830\sqrt{2}}{2}</math>. Therefore, our answer would be <math>1175-830+2+2=\fbox{\textbf{(D)} 349}</math>. | ||
Latest revision as of 14:03, 26 April 2021
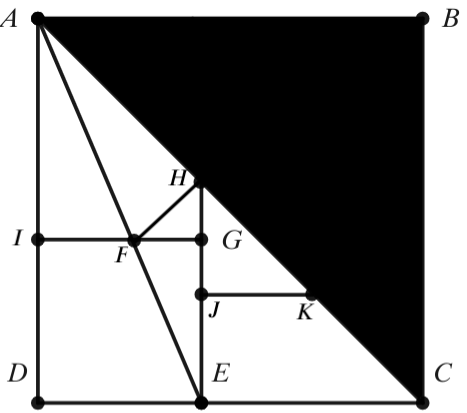
In the diagram, ![]() is a square with area
is a square with area ![]() .
. ![]() is a diagonal of square
is a diagonal of square ![]() . Square
. Square ![]() has area
has area ![]() . Given that point
. Given that point ![]() bisects line segment
bisects line segment ![]() , and
, and ![]() is a line segment. Extend
is a line segment. Extend ![]() to meet diagonal
to meet diagonal ![]() and mark the intersection point
and mark the intersection point ![]() . In addition,
. In addition, ![]() is drawn so that
is drawn so that ![]() .
. ![]() can be represented as
can be represented as ![]() where
where ![]() are not necessarily distinct integers. Given that
are not necessarily distinct integers. Given that ![]() , and
, and ![]() does not have a perfect square factor. Find
does not have a perfect square factor. Find ![]() .
.
![]()
Solution
To start this problem, we can first observe. Notice that ![]() is a right triangle because angle
is a right triangle because angle ![]() is supplementary to angle
is supplementary to angle ![]() which is a right angle. Therefore, we just have to solve for the length of side
which is a right angle. Therefore, we just have to solve for the length of side ![]() and
and ![]() .
.
Solve for ![]() :
Triangles
:
Triangles ![]() and
and ![]() are similar triangles, therefore, we can solve for length
are similar triangles, therefore, we can solve for length ![]() .
. ![]() . Use the technique of sum of squares and square root disintegration,
. Use the technique of sum of squares and square root disintegration, ![]() . Using the same technique,
. Using the same technique, ![]() .
. ![]() . Now, we can set up a ratio.
. Now, we can set up a ratio.
We can set ![]() , so
, so ![]() . Using the similar triangle,
. Using the similar triangle, ![]() . Plugging the numbers into the ratio, we can get
. Plugging the numbers into the ratio, we can get ![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
Solve for ![]() :
Since angle
:
Since angle ![]() is
is ![]() and angle
and angle ![]() is
is ![]() ,
, ![]() . Since
. Since ![]() ,
, ![]() .
Finally, we can solve for
.
Finally, we can solve for ![]() , that is,
, that is, ![]() . Therefore, our answer would be
. Therefore, our answer would be ![]() .
.