Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2004 AIME II Problems/Problem 11"

m
 
(18 intermediate revisions by 10 users not shown)
Line 1: Line 1:
 
== Problem ==
 
== Problem ==
−
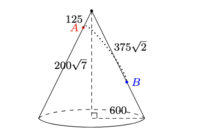
A right circular cone has a base with radius 600 and height <math> 200\sqrt{7}. </math> A fly starts at a point on the surface of the cone whose distance from the vertex of the cone is 125, and crawls along the surface of the cone to a point on the exact opposite side of the cone whose distance from the vertex is <math> 375\sqrt{2}. </math> Find the least distance that the fly could have crawled.
+
A [[right cone|right circular cone]] has a [[base]] with [[radius]] <math>600</math> and [[height]] <math> 200\sqrt{7}. </math> A fly starts at a point on the surface of the cone whose distance from the [[vertex]] of the cone is <math>125</math>, and crawls along the surface of the cone to a point on the exact opposite side of the cone whose distance from the vertex is <math>375\sqrt{2}.</math> Find the least distance that the fly could have crawled.
 +
 
 +
== Solution 1==
 +
The easiest way is to unwrap the cone into a circular sector. Center the sector at the origin with one radius on the positive <math>x</math>-axis and the angle <math>\theta</math> going counterclockwise. The circumference of the base is <math>C=1200\pi</math>. The sector's radius (cone's sweep) is <math>R=\sqrt{r^2+h^2}=\sqrt{600^2+(200\sqrt{7})^2}=\sqrt{360000+280000}=\sqrt{640000}=800</math>. Setting <math>\theta R=C\implies 800\theta=1200\pi\implies\theta=\frac{3\pi}{2}</math>.
 +
 
 +
If the starting point <math>A</math> is on the positive <math>x</math>-axis at <math>(125,0)</math> then we can take the end point <math>B</math> on <math>\theta</math>'s bisector at <math>\frac{3\pi}{4}</math> radians along the <math>y=-x</math> line in the second quadrant. Using the distance from the vertex puts <math>B</math> at <math>(-375,-375)</math>. Thus the shortest distance for the fly to travel is along segment <math>AB</math> in the sector, which gives a distance <math>\sqrt{(-375-125)^2+(-375-0)^2}=125\sqrt{4^2+3^2}=\boxed{625}</math>.
 +
 
 +
== Solution 2==
 +
[[File:2004_AIME_II_Problem_11_Diagram_1.png|200px|thumb|center]]
 +
 
 +
To find the shortest length from the red to blue points, the net of the side of the cone could be drawn.
 +
 
 +
[[File:2004_AIME_II_Problem_11_Diagram_2.png|200px|thumb|center]]
 +
 
 +
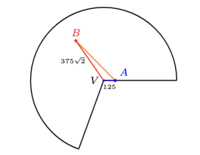
The angle <math>YVX</math> is equal to <math>360^\circ \cdot \frac{1200\pi}{1600\pi} \cdot \frac{1}{2}</math>, or <math>135^\circ</math>. Therefore, the law of cosines could be utilized.
 +
<cmath>
 +
AB = \sqrt{(375\sqrt{2})^2 + 125^2 - 2 \cdot (375\sqrt{2})(125)(\cos 135^\circ)} = \boxed{625}
 +
</cmath>
 +
 
 +
~Diagram and Solution by MaPhyCom
  
−
== Solution ==
 
−
Label the starting point of the fly as <math>A</math> and the ending as <math>B </math> and the vertex of the cone as <math>O</math>.With the give info <math>OA=125</math> and <math>OB=375\sqrt{2}</math> a By Pythagoras the slant height can be calculated by: <math>200\sqrt{7}^{2} + 600^2=640000 </math> so the slant height of the cone is 800.  The base of the cone has a circumference of <math>1200\pi</math>So if we cut the cone along its slant height and through <math>A</math> we get a sector of a circle <math>O</math> with radius 800. Now the sector is <math>\frac{1200\pi}{1600\pi}=\frac{3}{4}</math>. So the sector is 270 degrees. Now we know that <math>A</math> and <math>B</math> are on opposite sides therefore since <math>A</math> lies on a radius of the circle that is the "side" of a 270 degree sector B will lie exactly halfway between so the radius through B will divide the circle into two sectors each with measure 135. Draw in <math>BA</math> to create <math>\triangle{ABO}</math>. Now by Law of Cosines <math>AB^{2}=(125)^{2}+(375\sqrt{2})^{2}-2(125\cdot375\sqrt{2})(cos 135)</math> from there <math>AB=\sqrt{ (125)^{2}+(375\sqrt{2})^{2}-2(125\cdot375\sqrt{2})(cos 135)}=625</math>
 
 
== See also ==
 
== See also ==
−
* [[2004 AIME II Problems/Problem 10| Previous problem]]
+
{{AIME box|year=2004|n=II|num-b=10|num-a=12}}
−
* [[2004 AIME II Problems/Problem 12| Next problem]]
 
−
* [[2004 AIME II Problems]]
 
  
−
{{wikify}}
+
[[Category:Intermediate Geometry Problems]]
 +
{{MAA Notice}}

Latest revision as of 04:53, 25 June 2025

Problem

A right circular cone has a base with radius $600$ and height $200\sqrt{7}.$ A fly starts at a point on the surface of the cone whose distance from the vertex of the cone is $125$, and crawls along the surface of the cone to a point on the exact opposite side of the cone whose distance from the vertex is $375\sqrt{2}.$ Find the least distance that the fly could have crawled.

Solution 1

The easiest way is to unwrap the cone into a circular sector. Center the sector at the origin with one radius on the positive $x$-axis and the angle $\theta$ going counterclockwise. The circumference of the base is $C=1200\pi$. The sector's radius (cone's sweep) is $R=\sqrt{r^2+h^2}=\sqrt{600^2+(200\sqrt{7})^2}=\sqrt{360000+280000}=\sqrt{640000}=800$. Setting $\theta R=C\implies 800\theta=1200\pi\implies\theta=\frac{3\pi}{2}$.

If the starting point $A$ is on the positive $x$-axis at $(125,0)$ then we can take the end point $B$ on $\theta$'s bisector at $\frac{3\pi}{4}$ radians along the $y=-x$ line in the second quadrant. Using the distance from the vertex puts $B$ at $(-375,-375)$. Thus the shortest distance for the fly to travel is along segment $AB$ in the sector, which gives a distance $\sqrt{(-375-125)^2+(-375-0)^2}=125\sqrt{4^2+3^2}=\boxed{625}$.

Solution 2

2004 AIME II Problem 11 Diagram 1.png

To find the shortest length from the red to blue points, the net of the side of the cone could be drawn.

2004 AIME II Problem 11 Diagram 2.png

The angle $YVX$ is equal to $360^\circ \cdot \frac{1200\pi}{1600\pi} \cdot \frac{1}{2}$, or $135^\circ$. Therefore, the law of cosines could be utilized. \[AB = \sqrt{(375\sqrt{2})^2 + 125^2 - 2 \cdot (375\sqrt{2})(125)(\cos 135^\circ)} = \boxed{625}\]

~Diagram and Solution by MaPhyCom

See also

2004 AIME II (Problems • Answer Key • Resources)
Preceded by
Problem 10 		Followed by
Problem 12
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. AMC Logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2004_AIME_II_Problems/Problem_11&oldid=252218"