Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus
During AMC testing, the AoPS Wiki is in read-only mode and no edits can be made.

Difference between revisions of "2015 AIME I Problems/Problem 6"

(→‎See Also)
(→‎Solution 1: Clarified an equation)
 
(4 intermediate revisions by 2 users not shown)
Line 45: Line 45:
 
which when simplified yields <cmath>\frac{3x}{2}+12=\frac{3y}{2}</cmath> or <cmath>x+8=y</cmath>
 
which when simplified yields <cmath>\frac{3x}{2}+12=\frac{3y}{2}</cmath> or <cmath>x+8=y</cmath>
 
Since:
 
Since:
−
<cmath>5y=180-2x</cmath> and <cmath>5x+40=180-2x</cmath>
+
<cmath>\angle ACE=5y=180-2x</cmath> and <cmath>5x+40=180-2x</cmath>
 
So:
 
So:
 
<cmath>7x=140\Longleftrightarrow x=20</cmath>  
 
<cmath>7x=140\Longleftrightarrow x=20</cmath>  
Line 78: Line 78:
  
 
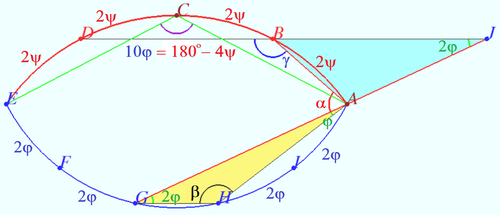
<cmath>BD||GH \implies \angle AJB = \angle AGH = 2 \varphi.</cmath>
 
<cmath>BD||GH \implies \angle AJB = \angle AGH = 2 \varphi.</cmath>
−
<cmath>\triangle AHG:  \angle AHG = \beta = 180^\circ – 3 \varphi </cmath>
+
<cmath>\triangle AHG: \hspace{10mm} \angle AHG = \beta = 180^\circ – 3 \varphi.</cmath>
−
<cmath>\triangle ABJ:  \angle ABD + \angle BAG = \alpha + \gamma = 180^\circ + 2 \varphi. </cmath>
+
<math>\hspace{10mm} \triangle ABJ:  \hspace{10mm} \angle BAG + \angle ABD = \alpha + \gamma = 180^\circ + 2 \varphi. </math>
 +
 
 
Let arc <math> \overset{\Large\frown} {AB} = 2\psi \implies</math>
 
Let arc <math> \overset{\Large\frown} {AB} = 2\psi \implies</math>
−
<math>\angle ACE = \frac {360^\circ – 8 \psi}{2}= 180^\circ – 4 \psi,  \angle ABD = \frac {360^\circ – 6 \psi}{2} =180^\circ – 3 \psi.</math>
 
−
<math>\beta – \gamma = 3(\varphi – \psi) = 12^\circ \implies \psi = \varphi – 4^\circ \implies 10 \varphi = 180^\circ – 4(\varphi – 4^\circ) \implies 14 \varphi = 168^\circ \implies \varphi = 12^\circ.</math>
 
  
−
Therefore <math>\gamma = 180^\circ – 3 \cdot (12^\circ – 4^\circ) = 156^\circ \implies  \alpha = 180^\circ + 2 \cdot 12^\circ – 156^\circ = \boxed{\textbf{058}}.</math>
+
<math>\angle ACE = \frac {360^\circ – 8 \psi}{2}= 180^\circ – 4 \psi,  \angle ABD = \gamma =\frac {360^\circ – 6 \psi}{2} =180^\circ – 3 \psi.</math>
 +
<math>\gamma –  \beta = 3(\varphi – \psi) = 12^\circ \implies \psi = \varphi – 4^\circ \implies 10 \varphi = 180^\circ – 4(\varphi – 4^\circ) \implies 14 \varphi = 196^\circ \implies \varphi = 14^\circ.</math>
 +
 
 +
Therefore <math>\gamma = 180^\circ – 3 \cdot (14^\circ – 4^\circ) = 150^\circ \implies  \alpha = 180^\circ + 2 \cdot 14^\circ – 150^\circ = \boxed{\textbf{058}}.</math>
 +
 
 +
 
 +
 
 +
==Video Solution==
 +
 
 +
https://youtu.be/IuwkX2Dv25s
 +
 
 +
~MathProblemSolvingSkills.com
 +
 
 +
 
  
 
==See Also==
 
==See Also==

Latest revision as of 01:37, 13 June 2025

Problem

Point $A,B,C,D,$ and $E$ are equally spaced on a minor arc of a circle. Points $E,F,G,H,I$ and $A$ are equally spaced on a minor arc of a second circle with center $C$ as shown in the figure below. The angle $\angle ABD$ exceeds $\angle AHG$ by $12^\circ$. Find the degree measure of $\angle BAG$.

[asy] pair A,B,C,D,E,F,G,H,I,O; O=(0,0); C=dir(90); B=dir(70); A=dir(50); D=dir(110); E=dir(130); draw(arc(O,1,50,130)); real x=2*sin(20*pi/180); F=x*dir(228)+C; G=x*dir(256)+C; H=x*dir(284)+C; I=x*dir(312)+C; draw(arc(C,x,200,340)); label("$A$",A,dir(0)); label("$B$",B,dir(75)); label("$C$",C,dir(90)); label("$D$",D,dir(105)); label("$E$",E,dir(180)); label("$F$",F,dir(225)); label("$G$",G,dir(260)); label("$H$",H,dir(280)); label("$I$",I,dir(315)); [/asy]

Solution 1

Let $O$ be the center of the circle with $ABCDE$ on it.

Let $x$ be the degree measurement of $\overarc{ED}=\overarc{DC}=\overarc{CB}=\overarc{BA}$ in circle $O$

and $y$ be the degree measurement of $\overarc{EF}=\overarc{FG}=\overarc{GH}=\overarc{HI}=\overarc{IA}$ in circle $C$.

$\angle ECA$ is, therefore, $5y$ by way of circle $C$ and \[\frac{360-4x}{2}=180-2x\] by way of circle $O$. $\angle ABD$ is $180 - \frac{3x}{2}$ by way of circle $O$, and \[\angle AHG = 180 - \frac{3y}{2}\] by way of circle $C$.

This means that:

\[180-\frac{3x}{2}=180-\frac{3y}{2}+12\]

which when simplified yields \[\frac{3x}{2}+12=\frac{3y}{2}\] or \[x+8=y\] Since: \[\angle ACE=5y=180-2x\] and \[5x+40=180-2x\] So: \[7x=140\Longleftrightarrow x=20\] \[y=28\] $\angle BAG$ is equal to $\angle BAE$ + $\angle EAG$, which equates to $\frac{3x}{2} + y$. Plugging in yields $30+28$, or $\boxed{058}$.

Solution 2

Let $m$ be the degree measurement of $\angle GCH$. Since $G,H$ lie on a circle with center $C$, $\angle GHC=\frac{180-m}{2}=90-\frac{m}{2}$.

Since $\angle ACH=2 \angle GCH=2m$, $\angle AHC=\frac{180-2m}{2}=90-m$. Adding $\angle GHC$ and $\angle AHC$ gives $\angle AHG=180-\frac{3m}{2}$, and $\angle ABD=\angle AHG+12=192-\frac{3m}{2}$. Since $AE$ is parallel to $BD$, $\angle DBA=180-\angle ABD=\frac{3m}{2}-12=$$\overarc{BE}$.

We are given that $A,B,C,D,E$ are evenly distributed on a circle. Hence,

$\overarc{ED}=\overarc{DC}=\overarc{CB}=\overarc{BA}$$=\frac{\angle DBA}{3}=\frac{m}{2}-4$

Here comes the key: Draw a line through $C$ parallel to $AE$, and select a point $X$ to the right of point $C$.

$\angle ACX$ = $\overarc{AB}$ + $\overarc{BC}$ = $m-8$.

Let the midpoint of $\overline{HG}$ be $Y$, then $\angle YCX=\angle ACX+\angle ACY=(m-8)+\frac{5m}{2}=90$. Solving gives $m=28$

The rest of the solution proceeds as in solution 1, which gives $\boxed{058}$


Solution 3

2015 AIME I 6.png

Let $\angle GAH = \varphi \implies \overset{\Large\frown} {GH} = 2\varphi \implies$ \[\overset{\Large\frown} {EF} = \overset{\Large\frown} {FG} = \overset{\Large\frown} {HI} = \overset{\Large\frown} {IA} = 2\varphi \implies\] \[\angle AGH = 2\varphi, \angle ACE = 10 \varphi.\]

\[BD||GH \implies \angle AJB = \angle AGH = 2 \varphi.\] \[\triangle AHG: \hspace{10mm} \angle AHG = \beta = 180^\circ – 3 \varphi.\] $\hspace{10mm} \triangle ABJ: \hspace{10mm} \angle BAG + \angle ABD = \alpha + \gamma = 180^\circ + 2 \varphi.$

Let arc $\overset{\Large\frown} {AB} = 2\psi \implies$

$\angle ACE = \frac {360^\circ – 8 \psi}{2}= 180^\circ – 4 \psi, \angle ABD = \gamma =\frac {360^\circ – 6 \psi}{2} =180^\circ – 3 \psi.$ $\gamma – \beta = 3(\varphi – \psi) = 12^\circ \implies \psi = \varphi – 4^\circ \implies 10 \varphi = 180^\circ – 4(\varphi – 4^\circ) \implies 14 \varphi = 196^\circ \implies \varphi = 14^\circ.$

Therefore $\gamma = 180^\circ – 3 \cdot (14^\circ – 4^\circ) = 150^\circ \implies \alpha = 180^\circ + 2 \cdot 14^\circ – 150^\circ = \boxed{\textbf{058}}.$


Video Solution

https://youtu.be/IuwkX2Dv25s

~MathProblemSolvingSkills.com


See Also

2015 AIME I (Problems • Answer Key • Resources)
Preceded by
Problem 5 		Followed by
Problem 7
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. AMC Logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2015_AIME_I_Problems/Problem_6&oldid=251081"