Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus
During AMC testing, the AoPS Wiki is in read-only mode and no edits can be made.

Difference between revisions of "2023 AMC 12B Problems/Problem 10"
(→‎Video Solution 1 by OmegaLearn)
 
(13 intermediate revisions by 7 users not shown)
Line 1: Line 1:
−
==Solution==
+
==Problem==
 +
In the <math>xy</math>-plane, a circle of radius <math>4</math> with center on the positive <math>x</math>-axis is tangent to the <math>y</math>-axis at the origin, and a circle with radius <math>10</math> with center on the positive <math>y</math>-axis is tangent to the <math>x</math>-axis at the origin. What is the slope of the line passing through the two points at which these circles intersect?
 +
 
 +
<math>\textbf{(A)}\ \dfrac{2}{7} \qquad\textbf{(B)}\ \dfrac{3}{7}  \qquad\textbf{(C)}\ \dfrac{2}{\sqrt{29}}  \qquad\textbf{(D)}\ \dfrac{1}{\sqrt{29}}  \qquad\textbf{(E)}\ \dfrac{2}{5}</math>
 +
 
 +
==Solution 1==
  
 
The center of the first circle is <math>(4,0)</math>.
 
The center of the first circle is <math>(4,0)</math>.
Line 6: Line 11:
  
 
Because this line is the perpendicular bisector of the line that passes through two intersecting points of two circles, the slope of the latter line is <math>\frac{-1}{- \frac{5}{2}} = \boxed{\textbf{(E) } \frac{2}{5}}</math>.
 
Because this line is the perpendicular bisector of the line that passes through two intersecting points of two circles, the slope of the latter line is <math>\frac{-1}{- \frac{5}{2}} = \boxed{\textbf{(E) } \frac{2}{5}}</math>.
 +
  
 
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
 
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
 +
 +
==Solution 2 (Coordinate Geometry)==
 +
 +
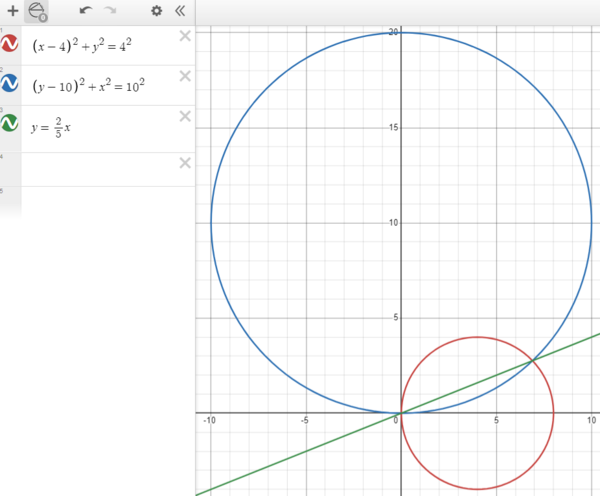
The first circle can be written as <math>(x-4)^2 + y^2 = 4^2</math> we'll call this equation <math>(1)</math>
 +
The second can we writen as <math>x^2 + (y-10)^2 = 10^2</math>, we'll call this equation <math>(2)</math>
 +
 +
Expanding <math>(1)</math>:
 +
<cmath>\begin{align*}
 +
x^2 -8x + 4^2 + y^2 &= 4^2 \\
 +
x^2 - 8x + y^2 &= 0
 +
\end{align*}</cmath>
 +
Exapnding <math>(2)</math>
 +
<cmath>\begin{align*}
 +
x^2 + y^2 -20y + 10^2 = 10^2\\
 +
x^2 + y^2 - 20y = 0
 +
\end{align*}</cmath>
 +
 +
Now we can set the equations equal to eachother:
 +
<cmath>\begin{align*}
 +
x^2 - 8x + y^2 &= x^2 + y^2 - 20y \\
 +
\frac{8}{20}x &= y \\
 +
\frac{2}{5}x &= y
 +
\end{align*}</cmath>
 +
This is in slope intercept form therefore the slope is <math>\boxed{\textbf{(E) } \frac{2}{5}}</math>.
 +
[[Image:Amc12B_2023_P10.PNG|thumb|center|600px]]
 +
~[https://artofproblemsolving.com/wiki/index.php/User:Cyantist luckuso]
 +
 +
==Video Solution 1 by OmegaLearn==
 +
https://youtu.be/IUB6r1iNgpU
 +
 +
==Video Solution==
 +
 +
https://youtu.be/sjJMWtL_CEY
 +
 +
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
 +
 +
==See Also==
 +
{{AMC12 box|year=2023|ab=B|num-b=9|num-a=11}}
 +
{{MAA Notice}}

Latest revision as of 19:59, 16 October 2025

Problem

In the $xy$-plane, a circle of radius $4$ with center on the positive $x$-axis is tangent to the $y$-axis at the origin, and a circle with radius $10$ with center on the positive $y$-axis is tangent to the $x$-axis at the origin. What is the slope of the line passing through the two points at which these circles intersect?

$\textbf{(A)}\ \dfrac{2}{7} \qquad\textbf{(B)}\ \dfrac{3}{7} \qquad\textbf{(C)}\ \dfrac{2}{\sqrt{29}} \qquad\textbf{(D)}\ \dfrac{1}{\sqrt{29}} \qquad\textbf{(E)}\ \dfrac{2}{5}$

Solution 1

The center of the first circle is $(4,0)$. The center of the second circle is $(0,10)$. Thus, the slope of the line that passes through these two centers is $- \frac{10}{4} = - \frac{5}{2}$.

Because this line is the perpendicular bisector of the line that passes through two intersecting points of two circles, the slope of the latter line is $\frac{-1}{- \frac{5}{2}} = \boxed{\textbf{(E) } \frac{2}{5}}$.


~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)

Solution 2 (Coordinate Geometry)

The first circle can be written as $(x-4)^2 + y^2 = 4^2$ we'll call this equation $(1)$ The second can we writen as $x^2 + (y-10)^2 = 10^2$, we'll call this equation $(2)$

Expanding $(1)$: \begin{align*} x^2 -8x + 4^2 + y^2 &= 4^2 \\ x^2 - 8x + y^2 &= 0 \end{align*} Exapnding $(2)$ \begin{align*} x^2 + y^2 -20y + 10^2 = 10^2\\ x^2 + y^2 - 20y = 0 \end{align*}

Now we can set the equations equal to eachother: \begin{align*} x^2 - 8x + y^2 &= x^2 + y^2 - 20y \\ \frac{8}{20}x &= y \\ \frac{2}{5}x &= y \end{align*} This is in slope intercept form therefore the slope is $\boxed{\textbf{(E) } \frac{2}{5}}$.

Amc12B 2023 P10.PNG

~luckuso

Video Solution 1 by OmegaLearn

https://youtu.be/IUB6r1iNgpU

Video Solution

https://youtu.be/sjJMWtL_CEY

~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)

See Also

2023 AMC 12B (Problems • Answer Key • Resources)
Preceded by
Problem 9 		Followed by
Problem 11
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. AMC Logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2023_AMC_12B_Problems/Problem_10&oldid=263289"