Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2023 AIME I Problems/Problem 15"

m (→‎Problem)
(→‎Solution 3)
 
(12 intermediate revisions by 6 users not shown)
Line 14: Line 14:
 
<cmath>1000>p=a^2+b^2\geq 12b^2+b^2=13b^2</cmath>so <math>b^2<81</math>, and <math>b<9</math>. If <math>b=8</math>, then <math>16\sqrt 3\leq a\leq 32</math>. Note that <math>\gcd(a,b)=1</math>, and <math>a\not\equiv b\pmod 2</math>, so <math>a=29</math> or <math>31</math>. However, then <math>5\mid a^2+b^2</math>, absurd.
 
<cmath>1000>p=a^2+b^2\geq 12b^2+b^2=13b^2</cmath>so <math>b^2<81</math>, and <math>b<9</math>. If <math>b=8</math>, then <math>16\sqrt 3\leq a\leq 32</math>. Note that <math>\gcd(a,b)=1</math>, and <math>a\not\equiv b\pmod 2</math>, so <math>a=29</math> or <math>31</math>. However, then <math>5\mid a^2+b^2</math>, absurd.
  
−
If <math>b=7</math>, by similar logic, we have that <math>14\sqrt 3 <a< 28</math>, so <math>b=26</math>. However, once again, <math>5\mid a^2+b^2</math>. If <math>b=6</math>, by the same logic, <math>12\sqrt3<a<24</math>, so <math>a=23</math>, where we run into the same problem. Thus <math>b\leq 5</math> indeed.
+
If <math>b=7</math>, by similar logic, we have that <math>14\sqrt 3 <a< 28</math>, so <math>a=26</math>. However, once again, <math>5\mid a^2+b^2</math>. If <math>b=6</math>, by the same logic, <math>12\sqrt3<a<24</math>, so <math>a=23</math>, where we run into the same problem. Thus <math>b\leq 5</math> indeed.
  
 
If <math>b=5</math>, note that
 
If <math>b=5</math>, note that
 
<cmath>(a+5)(a^2+25-20a)<a^2+25\implies a<20</cmath>We note that <math>p=5^2+18^2=349</math> works. Thus, we just need to make sure that if <math>b\leq 4</math>, <math>a\leq 18</math>. But this is easy, as
 
<cmath>(a+5)(a^2+25-20a)<a^2+25\implies a<20</cmath>We note that <math>p=5^2+18^2=349</math> works. Thus, we just need to make sure that if <math>b\leq 4</math>, <math>a\leq 18</math>. But this is easy, as
 
<cmath>p>(a+b)(a^2+b^2-4ab)\geq (4+18)(4^2+18^2-4\cdot 4\cdot 18)>1000</cmath>absurd. Thus, the answer is <math>\boxed{349}</math>.
 
<cmath>p>(a+b)(a^2+b^2-4ab)\geq (4+18)(4^2+18^2-4\cdot 4\cdot 18)>1000</cmath>absurd. Thus, the answer is <math>\boxed{349}</math>.
−
 
  
 
==Solution 2==
 
==Solution 2==
Line 47: Line 46:
 
</cmath>
 
</cmath>
  
−
We notice that <math>| z^3 | = p^{3/2}</math>, and <math>{\rm Re} \left( z^3 \right)</math>, <math>{\rm Im} \left( z^3 \right)</math>, and <math>| z^3 |</math> form a right triangle. Thus, <math>{\rm Re} z^3 + {\rm Im} z^3 > p^{3/2}</math>.
+
We notice that <math>| z^3 | = p^{3/2}</math>, and <math>{\rm Re} \left( z^3 \right)</math>, <math>{\rm Im} \left( z^3 \right)</math>, and <math>| z^3 |</math> form a right triangle. Thus, <math>{\rm Re} \left( z^3 \right) + {\rm Im} \left( z^3 \right) > p^{3/2}</math>.
 
Because <math>p > 1</math>, <math>p^{3/2} > p</math>.
 
Because <math>p > 1</math>, <math>p^{3/2} > p</math>.
 
Therefore, (3) holds.
 
Therefore, (3) holds.
Line 96: Line 95:
 
To facilitate efficient search, we apply the following criteria:
 
To facilitate efficient search, we apply the following criteria:
  
−
\begin{enumerate*}
+
To satisfy (7) and <math>a^2 + b^2 < 1000</math>, we have <math>1 \leq b \leq 15</math>.
−
\item To satisfy (7) and <math>a^2 + b^2 < 1000</math>, we have <math>1 \leq b \leq 15</math>.
 
 
In the outer layer, we search for <math>b</math> in a decreasing order.
 
In the outer layer, we search for <math>b</math> in a decreasing order.
 
In the inner layer, for each given <math>b</math>, we search for <math>a</math>.
 
In the inner layer, for each given <math>b</math>, we search for <math>a</math>.
−
\item Given <math>b</math>, we search for <math>a</math> in the range <math>\sqrt{3} b < a < \sqrt{1000 - b^2}</math>.
+
Given <math>b</math>, we search for <math>a</math> in the range <math>\sqrt{3} b < a < \sqrt{1000 - b^2}</math>.
−
\item We can prove that for <math>b \geq 9</math>, there is no feasible <math>a</math>.
+
We can prove that for <math>b \geq 9</math>, there is no feasible <math>a</math>.
 
The proof is as follows.
 
The proof is as follows.
  
Line 129: Line 127:
 
Therefore, we only need to consider <math>b \leq 8</math>.
 
Therefore, we only need to consider <math>b \leq 8</math>.
  
−
\item We eliminate <math>a</math> that are not relatively prime to <math>b</math>.
+
We eliminate <math>a</math> that is not relatively prime to <math>b</math>.
  
−
\item We use the following criteria to quickly eliminate <math>a</math> that make <math>a^2 + b^2</math> a composite number.
+
We use the following criteria to quickly eliminate <math>a</math> that make <math>a^2 + b^2</math> a composite number.
  
 
* For <math>b \equiv 1 \pmod{2}</math>, we eliminate <math>a</math> satisfying <math>a \equiv 1 \pmod{2}</math>.
 
* For <math>b \equiv 1 \pmod{2}</math>, we eliminate <math>a</math> satisfying <math>a \equiv 1 \pmod{2}</math>.
Line 149: Line 147:
  
 
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
 
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
 +
 +
==Solution 3==
 +
Let <math>z = a + b i (a,b\in I)</math>. <math>a^2 + b^2 = prime < 1000</math>, <math>(a,b) = 1</math>.
 +
 +
According to the question, <math>{\rm Re} \left( z^3 \right)</math>, <math>{\rm Im} \left( z^3 \right)</math>, and <math>|z^3|</math> construct the side-lengths of a non-degenerate triangle.
 +
 +
<math>z^3 = (a+bi)^3 = a^3+3a^2bi-3ab^2-b^3i = (a^3 - 3ab^2) + (3a^2b-b^3)i</math>
 +
 +
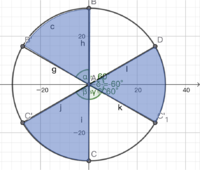
<math>{\rm Re} \left( z^3 \right) = a^3 - 3ab^2 > 0 => a(a^2 - 3b^2) > 0</math>
 +
 +
[[File:P15.png|200px]]
 +
 +
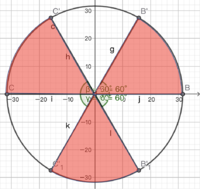
<math>{\rm Im} \left( z^3 \right) = a^3 - 3ab^2 > 0 => a(a^2 - 3b^2) > 0</math>
 +
 +
[[File:P15_2.png|200px]]
 +
 +
This means that the values of <math>a</math> and<math>b</math> should be limited in coincident areas these two graphs.
 +
 +
[[File:P15_1.png|350px]]
 +
 +
Also
 +
 +
<math>{\rm Re} \left( z^3 \right) + {\rm Im} \left( z^3 \right) > |z^3| > |z||z^2|>|z^2|</math>
 +
 +
<math>|{\rm Re} \left( z^3 \right) - {\rm Im} \left( z^3 \right)| < |z|^2</math>
 +
 +
<math>|a^3-3ab^2-(3a^2b-b^3)| < a^2+b^2</math>
 +
 +
<math>=|a^3-3ab^2+b^3-3a^2b|</math>
 +
 +
<math>=|a^3+b^3-3ab(a+b)|</math>
 +
 +
<math>=|a+b||a^2-4ab+b^2|<a^2+b^2 (*)</math>
 +
 +
If <math>a<0,b>0</math>, <math>|a^2-4ab+b^2|>|a^2+b^2|</math>, making statement <math>(*)</math> false.
 +
Combining with the former graph depicting possible ranges of <math>a,b</math>, by loss of generality, we assume <math>a,b</math> both <math>>0</math> and exists in the first <math>30^{\circ}</math> of the circle.
 +
 +
Let <math>\frac{a}{b} = \lambda > \sqrt{3}</math>.
 +
 +
<math>(*) |b^3(1+\lambda)\cdot({\lambda}^{2}-4\lambda+1)| < b^2(1+{\lambda}^{2})</math>
 +
 +
<math>b<|\frac{1+{\lambda}^2}{1+\lambda}|\cdot|\frac{1}{{\lambda}^{2}-4\lambda+1}|</math>
 +
 +
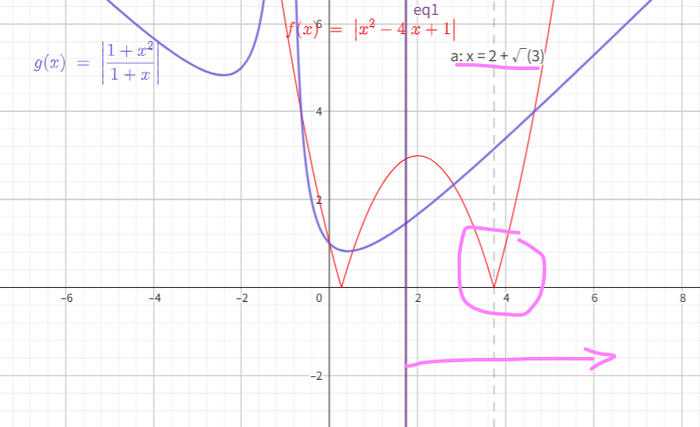
To clearly visualize, we graph out <math>|\frac{1+{\lambda}^2}{1+\lambda}|</math> and <math>|{\lambda}^{2}-4\lambda+1|</math> separately.
 +
 +
[[File:P15_full.png|700px]]
 +
 +
When <math>\lambda</math> is around <math>2+\sqrt{3}</math>, b reaches its maximum upper bound.
 +
 +
<math>b^2(1+{\lambda}^{2}) < 1000</math>
 +
 +
<math>b^2<66</math>
 +
 +
<math>b\le 8</math>
 +
 +
Testing values of <math>b</math> in decreasing order, starting from 8, we test out each corresponding value of <math>a</math>(<math>b\cdot\lambda</math>)by trying the two whole numbers closest to the real value of <math>a</math>.
 +
 +
We finally get that <math>b=5, a=18</math> and <math>p = 5^2+18^2 = \boxed{349}</math>
 +
 +
~cassphe
  
 
==Video Solution==
 
==Video Solution==

Latest revision as of 06:47, 3 June 2025

Problem

Find the largest prime number $p<1000$ for which there exists a complex number $z$ satisfying

  • the real and imaginary part of $z$ are both integers;
  • $|z|=\sqrt{p},$ and
  • there exists a triangle whose three side lengths are $p,$ the real part of $z^{3},$ and the imaginary part of $z^{3}.$

Solution

Assume that $z=a+bi$. Then, \[z^3=(a^3-3ab^2)+(3a^2b-b^3)i\]Note that by the Triangle Inequality, \[|(a^3-3ab^2)-(3a^2b-b^3)|<p\implies |a^3+b^3-3ab^2-3a^2b|<a^2+b^2\]Thus, we know \[|a+b||a^2+b^2-4ab|<a^2+b^2\]Without loss of generality, assume $a>b$ (as otherwise, consider $i^3\overline z=b+ai$). If $|a/b|\geq 4$, then \[17b^2\geq a^2+b^2>|a+b||a^2+b^2-4ab|\geq |b-4b||16b^2-16b^2+b^2|=3b^3\]`Thus, this means $b\leq\frac{17}3$ or $b\leq 5$. Also note that the roots of $x^2-4x+1$ are $2\pm\sqrt 3$, so thus if $b\geq 6$, \[2\sqrt 3b=(2(2-\sqrt 3)-4)b<a<4b\]Note that \[1000>p=a^2+b^2\geq 12b^2+b^2=13b^2\]so $b^2<81$, and $b<9$. If $b=8$, then $16\sqrt 3\leq a\leq 32$. Note that $\gcd(a,b)=1$, and $a\not\equiv b\pmod 2$, so $a=29$ or $31$. However, then $5\mid a^2+b^2$, absurd.

If $b=7$, by similar logic, we have that $14\sqrt 3 <a< 28$, so $a=26$. However, once again, $5\mid a^2+b^2$. If $b=6$, by the same logic, $12\sqrt3<a<24$, so $a=23$, where we run into the same problem. Thus $b\leq 5$ indeed.

If $b=5$, note that \[(a+5)(a^2+25-20a)<a^2+25\implies a<20\]We note that $p=5^2+18^2=349$ works. Thus, we just need to make sure that if $b\leq 4$, $a\leq 18$. But this is easy, as \[p>(a+b)(a^2+b^2-4ab)\geq (4+18)(4^2+18^2-4\cdot 4\cdot 18)>1000\]absurd. Thus, the answer is $\boxed{349}$.

Solution 2

Denote $z = a + i b$. Thus, $a^2 + b^2 = p$.

Thus, \[z^3 = a \left( a^2 - 3 b^2 \right) + i b \left( - b^2 + 3 a^2 \right) .\]

Because $p$, ${\rm Re} \left( z^3 \right)$, ${\rm Im} \left( z^3 \right)$ are three sides of a triangle, we have ${\rm Re} \left( z^3 \right) > 0$ and ${\rm Im} \left( z^3 \right) > 0$. Thus, \begin{align*} a \left( a^2 - 3 b^2 \right) & > 0 , \hspace{1cm} (1) \\ b \left( - b^2 + 3 a^2 \right) & > 0. \hspace{1cm} (2) \end{align*}

Because $p$, ${\rm Re} \left( z^3 \right)$, ${\rm Im} \left( z^3 \right)$ are three sides of a triangle, we have the following triangle inequalities: \begin{align*} {\rm Re} \left( z^3 \right) + {\rm Im} \left( z^3 \right) & > p \hspace{1cm} (3) \\ p + {\rm Re} \left( z^3 \right) & > {\rm Im} \left( z^3 \right) \hspace{1cm} (4) \\ p + {\rm Im} \left( z^3 \right) & > {\rm Re} \left( z^3 \right) \hspace{1cm} (5) \end{align*}

We notice that $| z^3 | = p^{3/2}$, and ${\rm Re} \left( z^3 \right)$, ${\rm Im} \left( z^3 \right)$, and $| z^3 |$ form a right triangle. Thus, ${\rm Re} \left( z^3 \right) + {\rm Im} \left( z^3 \right) > p^{3/2}$. Because $p > 1$, $p^{3/2} > p$. Therefore, (3) holds.

Conditions (4) and (5) can be written in the joint form as \[\left| {\rm Re} \left( z^3 \right) - {\rm Im} \left( z^3 \right) \right| < p . \hspace{1cm} (4)\]


We have \begin{align*} {\rm Re} \left( z^3 \right) - {\rm Im} \left( z^3 \right) & = \left( a^3 - 3 a b^2 \right) - \left( - b^3 + 3 a^2 b \right) \\ & = \left( a + b \right) \left( a^2 - 4 ab + b^2 \right) \end{align*} and $p = a^2 + b^2$.

Thus, (5) can be written as \[\left| \left( a + b \right) \left( a^2 - 4 ab + b^2 \right) \right| < a^2 + b^2 . \hspace{1cm} (6)\]

Therefore, we need to jointly solve (1), (2), (6). From (1) and (2), we have either $a, b >0$, or $a, b < 0$. In (6), by symmetry, without loss of generality, we assume $a, b > 0$.

Thus, (1) and (2) are reduced to \[a > \sqrt{3} b . \hspace{1cm} (7)\]

Let $a = \lambda b$. Plugging this into (6), we get \begin{align*} \left| \left( \left( \lambda - 2 \right)^2 - 3 \right) \right| < \frac{1}{b} \frac{\lambda^2 + 1}{\lambda + 1} . \hspace{1cm} (8) \end{align*}

Because $p= a^2 + b^2$ is a prime, $a$ and $b$ are relatively prime.

Therefore, we can use (7), (8), $a^2 + b^2 <1000$, and $a$ and $b$ are relatively prime to solve the problem.

To facilitate efficient search, we apply the following criteria:

To satisfy (7) and $a^2 + b^2 < 1000$, we have $1 \leq b \leq 15$. In the outer layer, we search for $b$ in a decreasing order. In the inner layer, for each given $b$, we search for $a$. Given $b$, we search for $a$ in the range $\sqrt{3} b < a < \sqrt{1000 - b^2}$. We can prove that for $b \geq 9$, there is no feasible $a$. The proof is as follows.

For $b \geq 9$, to satisfy $a^2 + b^2 < 1000$, we have $a \leq 30$. Thus, $\sqrt{3} < \lambda \leq \frac{30}{9}$. Thus, the R.H.S. of (8) has the following upper bound \begin{align*} \frac{1}{b} \frac{\lambda^2 + 1}{\lambda + 1} & < \frac{1}{b} \frac{\lambda^2 + \lambda}{\lambda + 1} \\ & = \frac{\lambda}{b} \\ & \leq \frac{\frac{30}{9}}{9} \\ & < \frac{10}{27} . \end{align*}

Hence, to satisfy (8), a necessary condition is \begin{align*} \left| \left( \left( \lambda - 2 \right)^2 - 3 \right) \right| < \frac{10}{27} . \end{align*}

However, this cannot be satisfied for $\sqrt{3} < \lambda \leq \frac{30}{9}$. Therefore, there is no feasible solution for $b \geq 9$. Therefore, we only need to consider $b \leq 8$.

We eliminate $a$ that is not relatively prime to $b$.

We use the following criteria to quickly eliminate $a$ that make $a^2 + b^2$ a composite number.

  • For $b \equiv 1 \pmod{2}$, we eliminate $a$ satisfying $a \equiv 1 \pmod{2}$.
  • For $b \equiv \pm 1 \pmod{5}$ (resp. $b \equiv \pm 2 \pmod{5}$), we eliminate $a$ satisfying $a \equiv \pm 2 \pmod{5}$ (resp. $a \equiv \pm 1 \pmod{5}$).


\item For the remaining $\left( b, a \right)$, check whether (8) and the condition that $a^2 + b^2$ is prime are both satisfied.

The first feasible solution is $b = 5$ and $a = 18$. Thus, $a^2 + b^2 = 349$.

\item For the remaining search, given $b$, we only search for $a \geq \sqrt{349 - b^2}$.

Following the above search criteria, we find the final answer as $b = 5$ and $a = 18$. Thus, the largest prime $p$ is $p = a^2 + b^2 = \boxed{\textbf{(349) }}$.

~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)

Solution 3

Let $z = a + b i (a,b\in I)$. $a^2 + b^2 = prime < 1000$, $(a,b) = 1$.

According to the question, ${\rm Re} \left( z^3 \right)$, ${\rm Im} \left( z^3 \right)$, and $|z^3|$ construct the side-lengths of a non-degenerate triangle.

$z^3 = (a+bi)^3 = a^3+3a^2bi-3ab^2-b^3i = (a^3 - 3ab^2) + (3a^2b-b^3)i$

${\rm Re} \left( z^3 \right) = a^3 - 3ab^2 > 0 => a(a^2 - 3b^2) > 0$

P15.png

${\rm Im} \left( z^3 \right) = a^3 - 3ab^2 > 0 => a(a^2 - 3b^2) > 0$

P15 2.png

This means that the values of $a$ and$b$ should be limited in coincident areas these two graphs.

P15 1.png

Also

${\rm Re} \left( z^3 \right) + {\rm Im} \left( z^3 \right) > |z^3| > |z||z^2|>|z^2|$

$|{\rm Re} \left( z^3 \right) - {\rm Im} \left( z^3 \right)| < |z|^2$

$|a^3-3ab^2-(3a^2b-b^3)| < a^2+b^2$

$=|a^3-3ab^2+b^3-3a^2b|$

$=|a^3+b^3-3ab(a+b)|$

$=|a+b||a^2-4ab+b^2|<a^2+b^2 (*)$

If $a<0,b>0$, $|a^2-4ab+b^2|>|a^2+b^2|$, making statement $(*)$ false. Combining with the former graph depicting possible ranges of $a,b$, by loss of generality, we assume $a,b$ both $>0$ and exists in the first $30^{\circ}$ of the circle.

Let $\frac{a}{b} = \lambda > \sqrt{3}$.

$(*) |b^3(1+\lambda)\cdot({\lambda}^{2}-4\lambda+1)| < b^2(1+{\lambda}^{2})$

$b<|\frac{1+{\lambda}^2}{1+\lambda}|\cdot|\frac{1}{{\lambda}^{2}-4\lambda+1}|$

To clearly visualize, we graph out $|\frac{1+{\lambda}^2}{1+\lambda}|$ and $|{\lambda}^{2}-4\lambda+1|$ separately.

P15 full.png

When $\lambda$ is around $2+\sqrt{3}$, b reaches its maximum upper bound.

$b^2(1+{\lambda}^{2}) < 1000$

$b^2<66$

$b\le 8$

Testing values of $b$ in decreasing order, starting from 8, we test out each corresponding value of $a$($b\cdot\lambda$)by trying the two whole numbers closest to the real value of $a$.

We finally get that $b=5, a=18$ and $p = 5^2+18^2 = \boxed{349}$

~cassphe

Video Solution

https://youtu.be/V0KFMIXmp08

~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)


Video Solution

https://youtu.be/tELK8fy36bs

~MathProblemSolvingSkills.com


Animated Video Solution

https://youtu.be/1Y8ql7eHt34

~Star League (https://starleague.us)


See also

2023 AIME I (Problems • Answer Key • Resources)
Preceded by
Problem 14 		Followed by
Last Problem
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. AMC Logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2023_AIME_I_Problems/Problem_15&oldid=249610"