Difference between revisions of "Markov Chains"

Latest revision as of 13:59, 21 July 2025

Markov Chains

Loosely put, a Markov Chain is a mathematical process involving transitions, governed by certain probabilistic rules, between different states. Markov chains are a special type of stochastic process that satisfy the Markov property, which states that the future state of the system depends only on its present state, and not on its history of past states. These types of systems appear frequently in math competitions, and are even more prevalent in various real-world applications.

Formulation

When a Markov chain "jumps" from one state to another, we call it a step. The number of steps a chain has undergone is conventionally denoted by a nonnegative index known as the time of the system. We use $S=\{1, 2, \cdots, N\}$ to denote all the possible states of the system, $t$ to denote the time index of the system, and $X_t$ to denote the state of the system at time $t$ . Notice that the state of the system at time $t$ is random, so $X_t$ is a random variable. Here, we assume that we are dealing with a discrete-time Markov chain, which is equivalent to assuming $t$ is an integer. To describe the probabilities for our process we need to calculate

$P\{X_0=i_0, X_1=i_1,\cdots, X_t=i_t\}$

for every $t$ and sequence of states $(i_0, i_1, \cdots, i_t)$ . Conditional probability tells us that the above is equal to

$P\{X_0=i_0\}P(X_1=i_1|X_0=i_0)P(X_2=i_2|X_0=i_0,X_1=i_1)\cdots P(X_t=i_t|X_0=i_0\cdots X_{t-1}=i_{t-1})$

Define

$\phi(i)=P\{X_0=i\}, i=1, \cdots, N$

We typically use $\phi(i)$ instead of $P\{X_0=i\}$ to simplify our notation. In reality, $\phi(i)$ is the initial probability distribution usually given by the context.

Since our process satisfies the Markov property, we know that $P(X_t=i_t|X_0=i_0\cdots X_{t-1}=i_{t-1})=P(X_t=i_t|X_{t-1}=i_{t-1})$

Now we make the additional assumption that $P(X_t=i|X_{t-1}=j)$ depends only on $i, j$ , but not $t$ . This assumption is called time homogeneity, and it just means that the "transition" probability from one state to another is invariant with respect to time. As a result, we can write $P(X_t=i|X_{t-1}=j)=p(i, j)$ for some function $p$ that from now on we will call the transition probability.

Using our new notation, it's not hard to see:

$P\{X_0=i_0, X_1=i_1,\cdots, X_t=i_t\}=p(i_t, i_{t-1})p(i_{t-1}, i_{t-2})\cdots p(i_1, i_0)\phi(i_0)$

Notice that $P\{X_0=i_0\}$ used to be our first term, but now it's our last term. Although we could have preserved the original order by using $p(j, i)$ instead of $p(i, j)$ (as seen in some textbooks), we choose to use $p(i, j)$ over $p(j, i)$ to avoid complications with matrix calculations that may arise later on.

Now consider the problem of calculating the probability distribution of $X_t$ for a given time $t$ and initial probability transition $\phi$ . There are several ways to approach this problem, all essentially the same, but different in form.

Approach 1 (Pure Matrix Multiplication)

Our goal is to calculate $P\{X_t=i_t\}$ for any given time $t$ and state $i_t$ . By using the law of total probability, or just intuition, it's easy to see:

$P\{X_t=i_t\}=\sum_{i_{t-1},\cdots,i_1, i_0\in S}^{} P\{X_0=i_0, X_1=i_1,\cdots, X_{t-1}=i_{t-1}, X_t=i_t\}$

$=\sum_{i_{t-1},\cdots,i_1, i_0\in S}^{} p(i_t, i_{t-1})p(i_{t-1}, i_{t-2})\cdots p(i_1, i_0)\phi(i_0)$

People well-versed in matrix multiplication will notice that the above summand is just the $i_t$ th term of the matrix product $\textbf{P}^t\phi$ , where $\phi$ is the initial probability distribution vector given by

\begin{equation} \phi = \begin{bmatrix} \phi(1) \\ \phi(2) \\ \vdots \\ \phi(N) \end{bmatrix} \end{equation}

and $\textbf{P}$ is the transition matrix given by

\begin{equation} \textbf{P} = \begin{bmatrix} p(1, 1) & p(1, 2) & \cdots & p(1, N) \\ p(2, 1) & p(2, 2) & \cdots & p(2, N) \\ \vdots \\ p(N, 1) & p(N, 2) & \cdots & p(N, N) \end{bmatrix} \end{equation}

$\textbf{P}^t\phi$ is a column vector, and we know from above that $P\{X_t=i_t\}=(\textbf{P}^t\phi)_{i_{t} 1}$ for any value of $i_t$ . Define $\phi_t(i)=P\{X_t=i\}$ , and

\begin{equation} \phi_t = \begin{bmatrix} \phi_t(1) \\ \phi_t(2) \\ \vdots \\ \phi_t(N) \end{bmatrix} \end{equation}

$\phi_t$ denotes the probability distribution of $X_t$ , and our results above can be rewritten as $\phi_t=\textbf{P}^t\phi$

~tsun26

Absorbing Markov Chains

This article is a stub. Help us out by expanding it.

Problems

Introductory

Problem 1

In the land of Markovia, there are three cities: $A$ , $B$ , and $C$ . There are 100 people who live in $A$ , 120 who live in $B$ , and 160 who live in $C$ . Everyone works in one of the three cities, and a person may work in the same city where they live. In the figure below, an arrow pointing from one city to another is labeled with the fraction of people living in the first city who work in the second city. (For example, $\frac{1}{4}$ of the people who live in $A$ work in $B$ .) How many people work in $A$ ?

$[asy] import graph; unitsize(2cm); real r=0.15; pair A, B, C;B = (0,0);C = (2,0);A = (1,sqrt(3)); // Drawing the nodes draw(circle(A,r)); label("$A$", A); draw(circle(B,r)); label("$B$", B); draw(circle(C,r)); label("$C$", C); guide AB=A+r*dir(-135)..{down}B+r*dir(90), BA=B+r*dir(60)..{up}A+r*dir(-105), BC=B+r*dir(0)..(1,-0.2)..C+r*dir(180), CB=C+r*dir(150)..(1,0.3)..B+r*dir(30), CA=C+r*dir(90){up}..A+r*dir(-45), AC=A+r*dir(-75){down}..C+r*dir(120); draw(AB,L=Label("$1/4$", MidPoint, W),Arrow(HookHead)); draw(BA,L=Label("$1/3$", MidPoint, W),Arrow(HookHead)); draw(BC,L=Label("$1/6$", MidPoint, S),Arrow(HookHead)); draw(CB,L=Label("$1/10$", MidPoint, S),Arrow(HookHead)); draw(CA,L=Label("$1/8$", MidPoint, E),Arrow(HookHead)); draw(AC,L=Label("$1/5$", MidPoint, E),Arrow(HookHead)); [/asy]$

$\textbf{(A)}\ 55\qquad \textbf{(B)}\ 60\qquad \textbf{(C)}\ 85\qquad \textbf{(D)}\ 115\qquad \textbf{(E)}\ 160$

(Source)

Problem 2

A cricket randomly hops between $4$ leaves, on each turn hopping to one of the other $3$ leaves with equal probability. After $4$ hops what is the probability that the cricket has returned to the leaf where it started?

$\textbf{(A) }\frac{2}{9}\qquad\textbf{(B) }\frac{19}{80}\qquad\textbf{(C) }\frac{20}{81}\qquad\textbf{(D) }\frac{1}{4}\qquad\textbf{(E) }\frac{7}{27}$

(Source)

Intermediate

Problem 1

Raashan, Sylvia, and Ted play the following game. Each starts with $$1$ . A bell rings every $15$ seconds, at which time each of the players who currently have money simultaneously chooses one of the other two players independently and at random and gives $$1$ to that player. What is the probability that after the bell has rung $2019$ times, each player will have $$1$ ? (For example, Raashan and Ted may each decide to give $$1$ to Sylvia, and Sylvia may decide to give her dollar to Ted, at which point Raashan will have $$0$ , Sylvia will have $$2$ , and Ted will have $$1$ , and that is the end of the first round of play. In the second round Rashaan has no money to give, but Sylvia and Ted might choose each other to give their $$1$ to, and the holdings will be the same at the end of the second round.)

$\textbf{(A) } \frac{1}{7} \qquad\textbf{(B) } \frac{1}{4} \qquad\textbf{(C) } \frac{1}{3} \qquad\textbf{(D) } \frac{1}{2} \qquad\textbf{(E) } \frac{2}{3}$

(Source)

Problem 2

Frieda the frog begins a sequence of hops on a $3 \times 3$ grid of squares, moving one square on each hop and choosing at random the direction of each hop-up, down, left, or right. She does not hop diagonally. When the direction of a hop would take Frieda off the grid, she "wraps around" and jumps to the opposite edge. For example if Frieda begins in the center square and makes two hops "up", the first hop would place her in the top row middle square, and the second hop would cause Frieda to jump to the opposite edge, landing in the bottom row middle square. Suppose Frieda starts from the center square, makes at most four hops at random, and stops hopping if she lands on a corner square. What is the probability that she reaches a corner square on one of the four hops?

$\textbf{(A)} ~\frac{9}{16}\qquad\textbf{(B)} ~\frac{5}{8}\qquad\textbf{(C)} ~\frac{3}{4}\qquad\textbf{(D)} ~\frac{25}{32}\qquad\textbf{(E)} ~\frac{13}{16}$

(Source)

Problem 3

In a small pond there are eleven lily pads in a row labeled 0 through 10. A frog is sitting on pad 1. When the frog is on pad $N$ , $0<N<10$ , it will jump to pad $N-1$ with probability $\frac{N}{10}$ and to pad $N+1$ with probability $1-\frac{N}{10}$ . Each jump is independent of the previous jumps. If the frog reaches pad 0 it will be eaten by a patiently waiting snake. If the frog reaches pad 10 it will exit the pond, never to return. What is the probability that the frog will escape without being eaten by the snake?

$\textbf{(A) }\frac{32}{79}\qquad \textbf{(B) }\frac{161}{384}\qquad \textbf{(C) }\frac{63}{146}\qquad \textbf{(D) }\frac{7}{16}\qquad \textbf{(E) }\frac{1}{2}\qquad$

(Source)

Problem 4

A bug starts at a vertex of a grid made of equilateral triangles of side length $1$ . At each step the bug moves in one of the $6$ possible directions along the grid lines randomly and independently with equal probability. What is the probability that after $5$ moves the bug never will have been more than $1$ unit away from the starting position?

$\textbf{(A)}\ \frac{13}{108} \qquad\textbf{(B)}\ \frac{7}{54} \qquad\textbf{(C)}\ \frac{29}{216} \qquad\textbf{(D)}\ \frac{4}{27} \qquad\textbf{(E)}\ \frac{1}{16}$

(Source)

Problem 5

A square is drawn in the Cartesian coordinate plane with vertices at $(2, 2)$ , $(-2, 2)$ , $(-2, -2)$ , $(2, -2)$ . A particle starts at $(0,0)$ . Every second it moves with equal probability to one of the eight lattice points (points with integer coordinates) closest to its current position, independently of its previous moves. In other words, the probability is $1/8$ that the particle will move from $(x, y)$ to each of $(x, y + 1)$ , $(x + 1, y + 1)$ , $(x + 1, y)$ , $(x + 1, y - 1)$ , $(x, y - 1)$ , $(x - 1, y - 1)$ , $(x - 1, y)$ , or $(x - 1, y + 1)$ . The particle will eventually hit the square for the first time, either at one of the 4 corners of the square or at one of the 12 lattice points in the interior of one of the sides of the square. The probability that it will hit at a corner rather than at an interior point of a side is $m/n$ , where $m$ and $n$ are relatively prime positive integers. What is $m + n$ ?

$\textbf{(A) } 4 \qquad\textbf{(B) } 5 \qquad\textbf{(C) } 7 \qquad\textbf{(D) } 15 \qquad\textbf{(E) } 39$

(Source)

Problem 6

Call a set of integers spacy if it contains no more than one out of any three consecutive integers. How many subsets of $\{1,2,3,\ldots,12\},$ including the empty set, are spacy?

$\mathrm{(A)}\ 121 \qquad \mathrm{(B)}\ 123 \qquad \mathrm{(C)}\ 125 \qquad \mathrm{(D)}\ 127 \qquad \mathrm{(E)}\ 129$

(Source)

Problem 7

Let $A$ , $B$ , $C$ and $D$ be the vertices of a regular tetrahedron, each of whose edges measures $1$ meter. A bug, starting from vertex $A$ , observes the following rule: at each vertex it chooses one of the three edges meeting at that vertex, each edge being equally likely to be chosen, and crawls along that edge to the vertex at its opposite end. Let $p = \frac{n}{729}$ be the probability that the bug is at vertex $A$ when it has crawled exactly $7$ meters. Find the value of $n$ .

(Source)

Problem 8

Let $A_1A_2A_3\ldots A_{12}$ be a dodecagon ( $12$ -gon). Three frogs initially sit at $A_4,A_8,$ and $A_{12}$ . At the end of each minute, simultaneously, each of the three frogs jumps to one of the two vertices adjacent to its current position, chosen randomly and independently with both choices being equally likely. All three frogs stop jumping as soon as two frogs arrive at the same vertex at the same time. The expected number of minutes until the frogs stop jumping is $\frac mn$ , where $m$ and $n$ are relatively prime positive integers. Find $m+n$ .

(Source)

Problem 9

A bug starts at a vertex of an equilateral triangle. On each move, it randomly selects one of the two vertices where it is not currently located, and crawls along a side of the triangle to that vertex. Given that the probability that the bug moves to its starting vertex on its tenth move is $m/n,$ where $m$ and $n$ are relatively prime positive integers, find $m + n.$

(Source)

Problem 10

Misha rolls a standard, fair six-sided die until she rolls $1-2-3$ in that order on three consecutive rolls. The probability that she will roll the die an odd number of times is $\dfrac{m}{n}$ where $m$ and $n$ are relatively prime positive integers. Find $m+n$ .

(Source)

This article is a stub. Help us out by expanding it.

Page

Toolbox

Search

Difference between revisions of "Markov Chains"

Latest revision as of 13:59, 21 July 2025

Contents

Markov Chains

Formulation

Approach 1 (Pure Matrix Multiplication)

Absorbing Markov Chains

Problems

Introductory

Problem 1

Problem 2

Intermediate

Problem 1

Problem 2

Problem 3

Problem 4

Problem 5

Problem 6

Problem 7

Problem 9

Problem 10

@@ Line 1: / Line 1: @@
 ==Markov Chains==
-  Loosely put a Markov Chain is a mathematical process involving transitions, governed by certain probabilistic rules, between different states. Markov chains are a special type of stochastic process that satisfy the Markov property, which states that the future state of the system depends only on its present state, and not on its history of past states. These types of systems appear frequently in math competitions, and are even more prevalent in various real-world applications.
+Loosely put, a Markov Chain is a mathematical process involving transitions, governed by certain probabilistic rules, between different states. Markov chains are a special type of stochastic process that satisfy the Markov property, which states that the future state of the system depends only on its present state, and not on its history of past states. These types of systems appear frequently in math competitions, and are even more prevalent in various real-world applications.
 ==Formulation==
-   When a Markov chain "jumps" from one state to another, we call it a step. The number of steps a chain has undergone is conventionally denoted by a nonnegative index known as the time of the system. We use <math>S=\{1, 2, \cdots, N\}</math> to denote all the possible states of the system, <math>t</math> to denote the time index of the system, and <math>X_t</math> to denote the state of the system at time <math>t</math>. Notice that the state of the system at time <math>t</math> is random, so <math>X_t</math> is a random variable. Here, we assume that we are dealing with a discrete-time Markov chain, which is equivalent to assuming <math>t</math> is an integer. To describe the probabilities for our process we need to calculate
+When a Markov chain "jumps" from one state to another, we call it a step. The number of steps a chain has undergone is conventionally denoted by a nonnegative index known as the time of the system. We use <math>S=\{1, 2, \cdots, N\}</math> to denote all the possible states of the system, <math>t</math> to denote the time index of the system, and <math>X_t</math> to denote the state of the system at time <math>t</math>. Notice that the state of the system at time <math>t</math> is random, so <math>X_t</math> is a random variable. Here, we assume that we are dealing with a discrete-time Markov chain, which is equivalent to assuming <math>t</math> is an integer. To describe the probabilities for our process we need to calculate
 <cmath>P\{X_0=i_0, X_1=i_1,\cdots, X_t=i_t\}</cmath>
@@ Line 29: / Line 29: @@
 Notice that <math>P\{X_0=i_0\}</math> used to be our first term, but now it's our last term. Although we could have preserved the original order by using <math>p(j, i)</math> instead of <math>p(i, j)</math> (as seen in some textbooks), we choose to use <math>p(i, j)</math> over <math>p(j, i)</math> to avoid complications with matrix calculations that may arise later on.
- Now consider the problem of calculating the probability distribution of <math>X_t</math> for a given time <math>t</math> and initial probability transition <math>\phi</math>. There are several ways to approach this problem, all essentially the same, but different in form.
+Now consider the problem of calculating the probability distribution of <math>X_t</math> for a given time <math>t</math> and initial probability transition <math>\phi</math>. There are several ways to approach this problem, all essentially the same, but different in form.
 ===Approach 1 (Pure Matrix Multiplication)===
@@ Line 80: / Line 80: @@
 <math>\phi_t</math> denotes the probability distribution of <math>X_t</math>, and our results above can be rewritten as <math>\phi_t=\textbf{P}^t\phi</math>
+~tsun26
+==Absorbing Markov Chains==
+{{stub}} <!-- Don't forget to remove the stub template at the bottom of the page. --[[User:Aoum|aoum]] -->
+==Problems==
+===Introductory===
+====Problem 1====
+In the land of Markovia, there are three cities: <math>A</math>, <math>B</math>, and <math>C</math>. There are 100 people who live in <math>A</math>, 120 who live in <math>B</math>, and 160 who live in <math>C</math>. Everyone works in one of the three cities, and a person may work in the same city where they live. In the figure below, an arrow pointing from one city to another is labeled with the fraction of people living in the first city who work in the second city. (For example, <math>\frac{1}{4}</math> of the people who live in <math>A</math> work in <math>B</math>.) How many people work in <math>A</math>?
+<asy>
+import graph;
+unitsize(2cm);
+real r=0.15;
+pair A, B, C;B = (0,0);C = (2,0);A = (1,sqrt(3));
+// Drawing the nodes
+draw(circle(A,r)); label("$A$", A);
+draw(circle(B,r)); label("$B$", B);
+draw(circle(C,r)); label("$C$", C);
+guide AB=A+r*dir(-135)..{down}B+r*dir(90),
+	  BA=B+r*dir(60)..{up}A+r*dir(-105),
+	  BC=B+r*dir(0)..(1,-0.2)..C+r*dir(180),
+      CB=C+r*dir(150)..(1,0.3)..B+r*dir(30),
+	  CA=C+r*dir(90){up}..A+r*dir(-45),
+	  AC=A+r*dir(-75){down}..C+r*dir(120);
+draw(AB,L=Label("$1/4$", MidPoint, W),Arrow(HookHead));
+draw(BA,L=Label("$1/3$", MidPoint, W),Arrow(HookHead));
+draw(BC,L=Label("$1/6$", MidPoint, S),Arrow(HookHead));
+draw(CB,L=Label("$1/10$", MidPoint, S),Arrow(HookHead));
+draw(CA,L=Label("$1/8$", MidPoint, E),Arrow(HookHead));
+draw(AC,L=Label("$1/5$", MidPoint, E),Arrow(HookHead));
+</asy>
+<math>\textbf{(A)}\ 55\qquad \textbf{(B)}\ 60\qquad \textbf{(C)}\ 85\qquad \textbf{(D)}\ 115\qquad \textbf{(E)}\ 160</math>
+([[2025_AMC_8_Problems/Problem_17|Source]])
+====Problem 2====
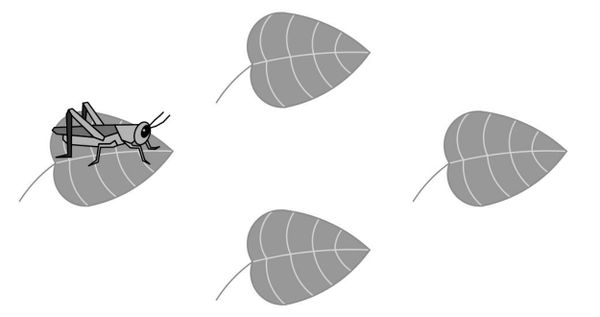
+A cricket randomly hops between <math>4</math> leaves, on each turn hopping to one of the other <math>3</math> leaves with equal probability. After <math>4</math> hops what is the probability that the cricket has returned to the leaf where it started?
+[[File:2022 AMC 8 Problem 25 Picture.jpg|center|600px]]
+<math>\textbf{(A) }\frac{2}{9}\qquad\textbf{(B) }\frac{19}{80}\qquad\textbf{(C) }\frac{20}{81}\qquad\textbf{(D) }\frac{1}{4}\qquad\textbf{(E) }\frac{7}{27}</math>
+([[2022 AMC 8 Problems/Problem 25|Source]])
+===Intermediate===
+====Problem 1====
+Raashan, Sylvia, and Ted play the following game. Each starts with <math> \$1</math>. A bell rings every <math>15</math> seconds, at which time each of the players who currently have money simultaneously chooses one of the other two players independently and at random and gives <math>\$1</math> to that player. What is the probability that after the bell has rung <math>2019</math> times, each player will have <math>\$1</math>? (For example, Raashan and Ted may each decide to give <math>\$1</math> to Sylvia, and Sylvia may decide to give her dollar to Ted, at which point Raashan will have <math>\$0</math>, Sylvia will have <math>\$2</math>, and Ted will have <math>\$1</math>, and that is the end of the first round of play. In the second round Rashaan has no money to give, but Sylvia and Ted might choose each other to give their <math> \$1</math> to, and the holdings will be the same at the end of the second round.)
+<math>\textbf{(A) } \frac{1}{7} \qquad\textbf{(B) } \frac{1}{4} \qquad\textbf{(C) } \frac{1}{3} \qquad\textbf{(D) } \frac{1}{2} \qquad\textbf{(E) } \frac{2}{3}</math>
+([[2019_AMC_10B_Problems/Problem_22|Source]])
+====Problem 2====
+Frieda the frog begins a sequence of hops on a <math>3 \times 3</math> grid of squares, moving one square on each hop and choosing at random the direction of each hop-up, down, left, or right. She does not hop diagonally. When the direction of a hop would take Frieda off the grid, she "wraps around" and jumps to the opposite edge. For example if Frieda begins in the center square and makes two hops "up", the first hop would place her in the top row middle square, and the second hop would cause Frieda to jump to the opposite edge, landing in the bottom row middle square. Suppose Frieda starts from the center square, makes at most four hops at random, and stops hopping if she lands on a corner square. What is the probability that she reaches a corner square on one of the four hops?
+<math>\textbf{(A)} ~\frac{9}{16}\qquad\textbf{(B)} ~\frac{5}{8}\qquad\textbf{(C)} ~\frac{3}{4}\qquad\textbf{(D)} ~\frac{25}{32}\qquad\textbf{(E)} ~\frac{13}{16}</math>
+([[2021 AMC 12A Problems/Problem 23|Source]])
+====Problem 3====
+In a small pond there are eleven lily pads in a row labeled 0 through 10.  A frog is sitting on pad 1.  When the frog is on pad <math>N</math>, <math>0<N<10</math>, it will jump to pad <math>N-1</math> with probability <math>\frac{N}{10}</math> and to pad <math>N+1</math> with probability <math>1-\frac{N}{10}</math>.  Each jump is independent of the previous jumps.  If the frog reaches pad 0 it will be eaten by a patiently waiting snake.  If the frog reaches pad 10 it will exit the pond, never to return.  What is the probability that the frog will escape without being eaten by the snake?
+<math>\textbf{(A) }\frac{32}{79}\qquad
+\textbf{(B) }\frac{161}{384}\qquad
+\textbf{(C) }\frac{63}{146}\qquad
+\textbf{(D) }\frac{7}{16}\qquad
+\textbf{(E) }\frac{1}{2}\qquad</math>
+([[2014 AMC 10B Problems/Problem 25|Source]])
+====Problem 4====
+A bug starts at a vertex of a grid made of equilateral triangles of side length <math>1</math>. At each step the bug moves in one of the <math>6</math> possible directions along the grid lines randomly and independently with equal probability. What is the probability that after <math>5</math> moves the bug never will have been more than <math>1</math> unit away from the starting position?
+<math>\textbf{(A)}\ \frac{13}{108} \qquad\textbf{(B)}\  \frac{7}{54} \qquad\textbf{(C)}\  \frac{29}{216} \qquad\textbf{(D)}\
+\frac{4}{27} \qquad\textbf{(E)}\ \frac{1}{16}</math>
+([[2021 Fall AMC 12B Problems/Problem 17|Source]])
+====Problem 5====
+A square is drawn in the Cartesian coordinate plane with vertices at <math>(2, 2)</math>, <math>(-2, 2)</math>, <math>(-2, -2)</math>, <math>(2, -2)</math>. A particle starts at <math>(0,0)</math>. Every second it moves with equal probability to one of the eight lattice points (points with integer coordinates) closest to its current position, independently of its previous moves. In other words, the probability is <math>1/8</math> that the particle will move from <math>(x, y)</math> to each of <math>(x, y + 1)</math>, <math>(x + 1, y + 1)</math>, <math>(x + 1, y)</math>, <math>(x + 1, y - 1)</math>, <math>(x, y - 1)</math>, <math>(x - 1, y - 1)</math>, <math>(x - 1, y)</math>, or <math>(x - 1, y + 1)</math>. The particle will eventually hit the square for the first time, either at one of the 4 corners of the square or at one of the 12 lattice points in the interior of one of the sides of the square. The probability that it will hit at a corner rather than at an interior point of a side is <math>m/n</math>, where <math>m</math> and <math>n</math> are relatively prime positive integers. What is <math>m + n</math>?
+<math> \textbf{(A) } 4 \qquad\textbf{(B) } 5 \qquad\textbf{(C) } 7 \qquad\textbf{(D) } 15 \qquad\textbf{(E) } 39 </math>
+([[2017 AMC 12A Problems/Problem 22|Source]])
+====Problem 6====
+Call a set of integers ''spacy'' if it contains no more than one out of any three consecutive integers. How many [[subset]]s of <math>\{1,2,3,\ldots,12\},</math> including the [[empty set]], are spacy?
+<math>\mathrm{(A)}\ 121 \qquad \mathrm{(B)}\ 123 \qquad \mathrm{(C)}\ 125 \qquad \mathrm{(D)}\ 127 \qquad \mathrm{(E)}\ 129</math>
+([[2007 AMC 12A Problems/Problem 25|Source]])
+====Problem 7====
+Let <math>A</math>, <math>B</math>, <math>C</math> and <math>D</math> be the vertices of a regular tetrahedron, each of whose edges measures <math>1</math> meter. A bug, starting from vertex <math>A</math>, observes the following rule: at each vertex it chooses one of the three edges meeting at that vertex, each edge being equally likely to be chosen, and crawls along that edge to the vertex at its opposite end. Let <math>p = \frac{n}{729}</math> be the probability that the bug is at vertex <math>A</math> when it has crawled exactly <math>7</math> meters. Find the value of <math>n</math>.
+([[1985 AIME Problems/Problem 12|Source]])
+'''Problem 8'''
+Let <math>A_1A_2A_3\ldots A_{12}</math> be a dodecagon (<math>12</math>-gon). Three frogs initially sit at <math>A_4,A_8,</math> and <math>A_{12}</math>. At the end of each minute, simultaneously, each of the three frogs jumps to one of the two vertices adjacent to its current position, chosen randomly and independently with both choices being equally likely. All three frogs stop jumping as soon as two frogs arrive at the same vertex at the same time. The expected number of minutes until the frogs stop jumping is <math>\frac mn</math>, where <math>m</math> and <math>n</math> are relatively prime positive integers. Find <math>m+n</math>.
+([[2021 AIME I Problems/Problem 12|Source]])
+====Problem 9====
+A bug starts at a vertex of an equilateral triangle. On each move, it randomly selects one of the two vertices where it is not currently located, and crawls along a side of the triangle to that vertex. Given that the probability that the bug moves to its starting vertex on its tenth move is <math>m/n,</math> where <math>m</math> and <math>n</math> are relatively prime positive integers, find <math>m + n.</math>
+([[2003 AIME II Problems/Problem 13|Source]])
+====Problem 10====
+Misha rolls a standard, fair six-sided die until she rolls <math>1-2-3</math> in that order on three consecutive rolls. The probability that she will roll the die an odd number of times is <math>\dfrac{m}{n}</math> where <math>m</math> and <math>n</math> are relatively prime positive integers. Find <math>m+n</math>.
+([[2018 AIME II Problems/Problem 13|Source]])
+{{stub}} <!-- Don't forget to remove the stub template in the Absorbing Markov Chains section. --[[User:Aoum|aoum]] -->