Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2024 AMC 10A Problems/Problem 25"

m (→‎Best Solution 1)
(→‎(Best) Solution 1)
 
(29 intermediate revisions by 13 users not shown)
Line 19: Line 19:
 
<math>\textbf{(A) }130\qquad\textbf{(B) }144\qquad\textbf{(C) }146\qquad\textbf{(D) }162\qquad\textbf{(E) }196</math>
 
<math>\textbf{(A) }130\qquad\textbf{(B) }144\qquad\textbf{(C) }146\qquad\textbf{(D) }162\qquad\textbf{(E) }196</math>
  
−
==(Best) Solution 1==
+
== Solution 1 (Best Motivated)==
  
  
 
Observations:  
 
Observations:  
  
−
1. You can not have a vertical line in any place other than the first and second columns and the last and second-to-last columns.
+
1. You can not have a vertical line in any place other than the first two columns and the last two columns. If we did, we would have at least one of the middle cells with toothpicks along more than one side, which would violate the conditions of the problem.
  
−
2. You can you a box around the top row or along the bottom row, otherwise all the solutions have a vertical line at the first and second columns and the last and second-to-last columns.
+
2. There are two cases that look completely different. We can have a long horizontal box that spans all eight cells either on top of or below the middle cells, or we have to have a shape that looks like a rectangle, except with a few places "pushed" in.  
  
−
Thus, Using casework, we can split this problem into 4 cases. However, we can focus on only the first one for right now.  
+
Thus, using casework, we can split the task of finding those rectangles with squiggly edges into 3 cases.
  
−
For case 1, we assume that the green lines shown below are given (always have toothpicks on them)
+
For case 1, we assume that the green lines shown below are given (always have toothpicks on them). In effect, we will use all eight columns.
  
 
[[Image:Scrasdfasd.png|600px]]
 
[[Image:Scrasdfasd.png|600px]]
Line 36: Line 36:
 
[[Image:Screenshot 2024-11-08 192200.png|600px]]
 
[[Image:Screenshot 2024-11-08 192200.png|600px]]
  
−
And the only toothpicks we can place that will connect to the red lines are to go horizontally inward:
+
The only toothpicks we can place that will connect to the red lines are to go horizontally inward:
  
 
[[Image:Screenshot 2024-11-08 192516.png|600px]]
 
[[Image:Screenshot 2024-11-08 192516.png|600px]]
  
−
Now, concentrate on the first row of squares. A toothpick can be placed on either the bottom or top and connected to a continuous squiggle by adding vertical toothpicks, for example,
+
Now, concentrate on the first row of squares. A toothpick can be placed on either the bottom or top and connected to a continuous squiggle by adding vertical toothpicks:
  
 
[[Image:Screenshot 2024-11-08 193401.png|600px]]
 
[[Image:Screenshot 2024-11-08 193401.png|600px]]
Line 48: Line 48:
 
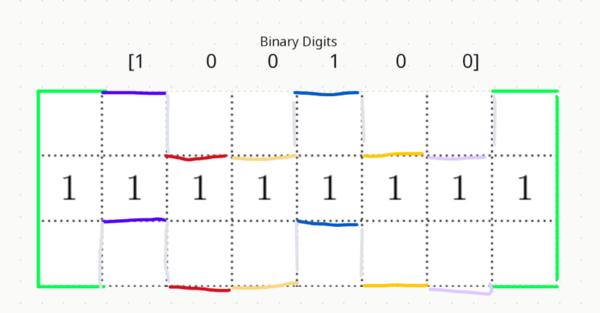
[[Image:Screenshot 2024-11-08 194804.png|600px]]
 
[[Image:Screenshot 2024-11-08 194804.png|600px]]
  
−
We can summarize this by giving a high squiggle position a 1 and a low position a 0, thus we have a 6-digit binary sequence. Thus, we can have <math>2^6=64</math> ways to make this squiggle.  
+
We can summarize this by giving a high squiggle position a 1 and a low position a 0, thus we have a 6-digit binary sequence. Thus, we can have <math>2^6=64</math> ways to make this squiggle. (The binary is not absolutely necessary, but it works.) 
  
−
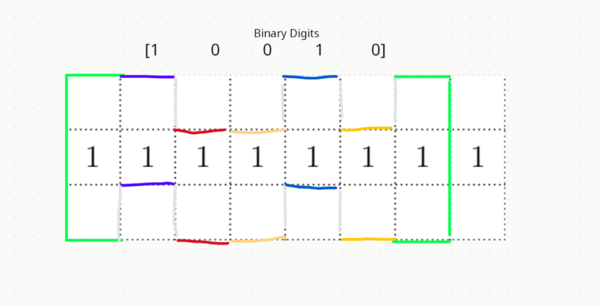
Case 2: We can also, as the observations state, pull in one of the sides, thus we can have a squiggle with 5 binary digits. only utilizing the first 7 columns:
+
Case 2: We can also pull in one of the sides, thus we can have a squiggle with 5 binary digits, which only uses the first or last 7 columns:
  
 
[[Image:Screenshot 2024-11-08 195135.png|600px]]
 
[[Image:Screenshot 2024-11-08 195135.png|600px]]
−
 
−
Here, we only have 5 binary digits to work with, so there are <math>2^5=32</math> ways to make this squiggle.
 
−
 
−
Case 3: Similarly, we can utilize the last 7 columns.
 
  
 
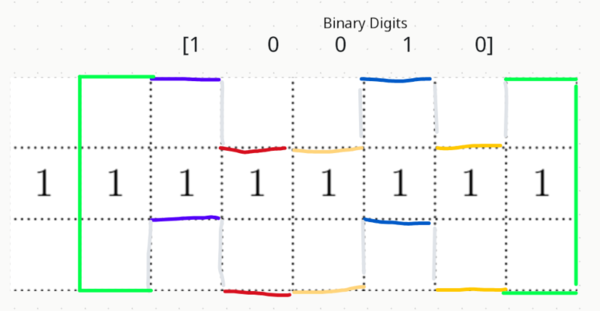
[[Image:Screenshot 2024-11-08 195553.png|600px]]
 
[[Image:Screenshot 2024-11-08 195553.png|600px]]
  
−
Again, we only have 5 binary digits to work with, so there are <math>2^5=32</math> ways to make this squiggle.  
+
Here, we only have 5 binary digits to work with, so there are <math>2^5=32</math> ways to make this squiggle for each individual subcase. There are two subcases, one with the first 7 columns, and the other with the last 7, so we have a total of <math>32\cdot 2 = 64</math> arrangements in this case.
  
−
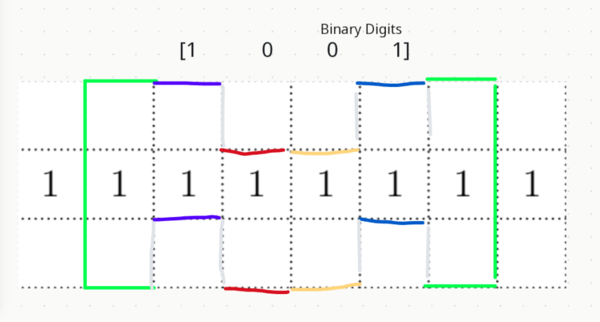
Case 4: We can use an even smaller section. Using only the middle 6 columns gives us a 4-wide squiggle:
+
Case 3: We can use an even smaller section. Using only the middle 6 columns gives us a 4-wide squiggle:
  
 
[[Image:Screenshot 2024-11-08 195945.png|600px]]
 
[[Image:Screenshot 2024-11-08 195945.png|600px]]
Line 68: Line 64:
 
Thus, there are <math>2^4=16</math> ways to make this squiggle.  
 
Thus, there are <math>2^4=16</math> ways to make this squiggle.  
  
−
Adding up all our cases: <math>64+32+32+16=144</math>
+
These three cases together cover all loops of this form. If we try to bring the square bracket like shapes on each side any closer, there will be some middle cells that do not touch any toothpicks. Adding up all our cases for these types of shapes: <math>64+32+32+16=144</math>.
  
 
However, there are two more ways to draw a qualifying shape:
 
However, there are two more ways to draw a qualifying shape:
Line 74: Line 70:
 
[[Image:Screenshot 2024-11-08 200416.png|600px]]
 
[[Image:Screenshot 2024-11-08 200416.png|600px]]
  
−
We can draw a rectangle like that in the first row or third row. Thus, we have a grand total of  
+
We can draw a rectangle like that in the first row or third row. Thus, we have a total of  
 
<math>144+2=\boxed{\textbf{(C) }146}</math> ways.
 
<math>144+2=\boxed{\textbf{(C) }146}</math> ways.
  
Line 83: Line 79:
 
~hermanboxcar5
 
~hermanboxcar5
  
−
==Solution 3 (Cheese)==
+
Notes:
 +
Remember these are the ONLY possible cases. It is impossible to cross through the rows of boxes of ones (in a snake like pattern) to connect the loop around the bottom since then the loop would intersect itself.
 +
 
 +
We are not undercounting by only counting the binary digits on the top. Consider the top squiggle. Each middle square must and can only come in contact with one toothpick, so if the top squiggle doesn't touch a specific middle cell, the bottom squiggle must to ensure that all squares touch one toothpick.
 +
~juwushu
 +
 
 +
~LeonQS (additional clarity and precision)
 +
 
 +
==Solution 2 (Cheese)==
 
Notice that for any case where the closed loop does not connect from the top side of the ones and bottom side of the ones, there are two of these cases. A cheese solution can be found from this; noting that B and C are the only two options to each other, and, being two apart, with people likely to forget this case, <math>\boxed{\textbf{(C) }146}</math> is likely to be the correct answer.
 
Notice that for any case where the closed loop does not connect from the top side of the ones and bottom side of the ones, there are two of these cases. A cheese solution can be found from this; noting that B and C are the only two options to each other, and, being two apart, with people likely to forget this case, <math>\boxed{\textbf{(C) }146}</math> is likely to be the correct answer.
 
Cheese solution done by [[User:Juwushu|juwushu]].
 
Cheese solution done by [[User:Juwushu|juwushu]].
  
−
==See also==
+
==Solution 3 (Observation)==
−
{{AMC10 box|year=2024|ab=A|num-b=24|after=Last Problem}}
+
 
−
{{AMC12 box|year=2024|ab=A|num-b=21|num-a=23}}
+
We have <math>2</math> cases where the loop does not go through the middle.
 +
 
 +
If the loop goes through the middle, we must have a full column on <math>(0,8),(0,7),(1,8),(1,7).</math> Then we have <math>6,5,5,4</math> empty middle squares. For each one we can have one on top or one on bottom, so <math>2^6+2^5+2^5+2^4=144.</math> Notice that for each case of fixed toothpicks, there is only one way to form the loop. Then we just add <math>2+144=\boxed{\textbf{(C) } 146.}</math>
 +
 
 +
~nevergonnagiveup
 +
 
 +
== Video Solution by Power Solve ==
 +
https://www.youtube.com/watch?v=FRNbJ5wIGRo
 +
 
 +
==Video Solution By SpreadTheMathLove==
 +
https://www.youtube.com/watch?v=huMQ9J7rIj0&t=77s
 +
 
 +
== Video solution by TheNeuralMathAcademy ==
 +
https://www.youtube.com/watch?v=4b_YLnyegtw&t=5850s
 +
 
 +
==See Also==
 +
{{AMC10 box|year=2024|ab=A|before=[[2023 AMC 10B Problems]]|after=[[2024 AMC 10B Problems]]}}
 +
* [[AMC 10]]
 +
* [[AMC 10 Problems and Solutions]]
 +
* [[Mathematics competitions]]
 +
* [[Mathematics competition resources]]
 
{{MAA Notice}}
 
{{MAA Notice}}

Latest revision as of 15:50, 23 August 2025

The following problem is from both the 2024 AMC 10A #25 and 2024 AMC 12A #22, so both problems redirect to this page.

Problem

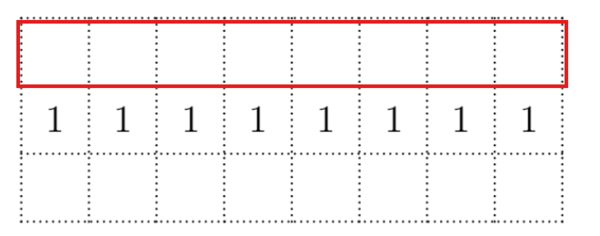
The figure below shows a dotted grid $8$ cells wide and $3$ cells tall consisting of $1''\times1''$ squares. Carl places $1$-inch toothpicks along some of the sides of the squares to create a closed loop that does not intersect itself. The numbers in the cells indicate the number of sides of that square that are to be covered by toothpicks, and any number of toothpicks are allowed if no number is written. In how many ways can Carl place the toothpicks? [asy] size(6cm); for (int i=0; i<9; ++i) { draw((i,0)--(i,3),dotted); } for (int i=0; i<4; ++i){ draw((0,i)--(8,i),dotted); } for (int i=0; i<8; ++i) { for (int j=0; j<3; ++j) { if (j==1) { label("1",(i+0.5,1.5)); }}} [/asy] $\textbf{(A) }130\qquad\textbf{(B) }144\qquad\textbf{(C) }146\qquad\textbf{(D) }162\qquad\textbf{(E) }196$

Solution 1 (Best Motivated)

Observations:

1. You can not have a vertical line in any place other than the first two columns and the last two columns. If we did, we would have at least one of the middle cells with toothpicks along more than one side, which would violate the conditions of the problem.

2. There are two cases that look completely different. We can have a long horizontal box that spans all eight cells either on top of or below the middle cells, or we have to have a shape that looks like a rectangle, except with a few places "pushed" in.

Thus, using casework, we can split the task of finding those rectangles with squiggly edges into 3 cases.

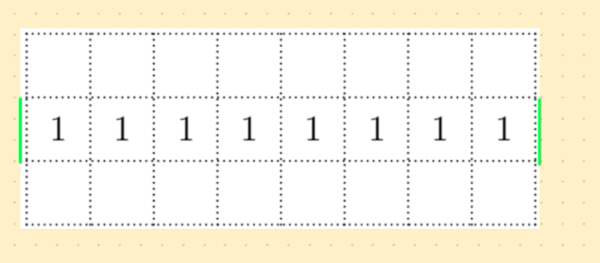
For case 1, we assume that the green lines shown below are given (always have toothpicks on them). In effect, we will use all eight columns.

Scrasdfasd.png

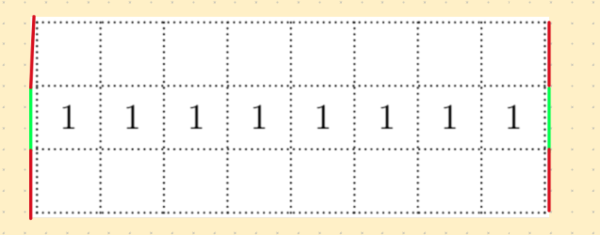
Screenshot 2024-11-08 192200.png

The only toothpicks we can place that will connect to the red lines are to go horizontally inward:

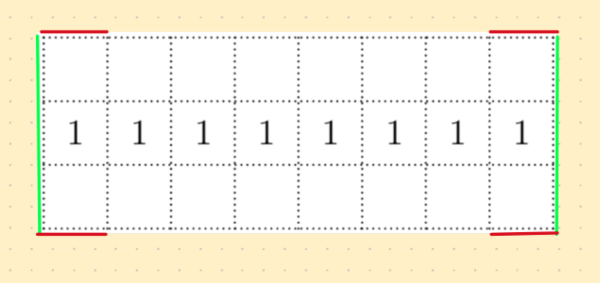
Screenshot 2024-11-08 192516.png

Now, concentrate on the first row of squares. A toothpick can be placed on either the bottom or top and connected to a continuous squiggle by adding vertical toothpicks:

Screenshot 2024-11-08 193401.png

How many squiggles are possible?

Screenshot 2024-11-08 194804.png

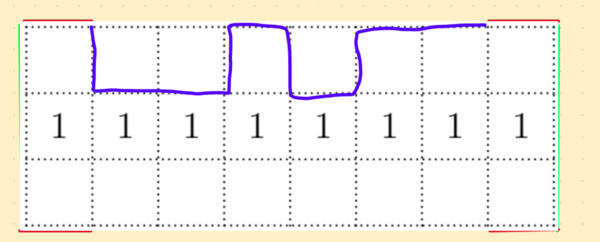
We can summarize this by giving a high squiggle position a 1 and a low position a 0, thus we have a 6-digit binary sequence. Thus, we can have $2^6=64$ ways to make this squiggle. (The binary is not absolutely necessary, but it works.)

Case 2: We can also pull in one of the sides, thus we can have a squiggle with 5 binary digits, which only uses the first or last 7 columns:

Screenshot 2024-11-08 195135.png

Screenshot 2024-11-08 195553.png

Here, we only have 5 binary digits to work with, so there are $2^5=32$ ways to make this squiggle for each individual subcase. There are two subcases, one with the first 7 columns, and the other with the last 7, so we have a total of $32\cdot 2 = 64$ arrangements in this case.

Case 3: We can use an even smaller section. Using only the middle 6 columns gives us a 4-wide squiggle:

Screenshot 2024-11-08 195945.png

Thus, there are $2^4=16$ ways to make this squiggle.

These three cases together cover all loops of this form. If we try to bring the square bracket like shapes on each side any closer, there will be some middle cells that do not touch any toothpicks. Adding up all our cases for these types of shapes: $64+32+32+16=144$.

However, there are two more ways to draw a qualifying shape:

Screenshot 2024-11-08 200416.png

We can draw a rectangle like that in the first row or third row. Thus, we have a total of $144+2=\boxed{\textbf{(C) }146}$ ways.


A note to (potential) editors: This answer was not made to be concise or especially professional. It was made to explicitly explain this problem in a way so that it is easy to understand and follow.

~hermanboxcar5

Notes: Remember these are the ONLY possible cases. It is impossible to cross through the rows of boxes of ones (in a snake like pattern) to connect the loop around the bottom since then the loop would intersect itself.

We are not undercounting by only counting the binary digits on the top. Consider the top squiggle. Each middle square must and can only come in contact with one toothpick, so if the top squiggle doesn't touch a specific middle cell, the bottom squiggle must to ensure that all squares touch one toothpick. ~juwushu

~LeonQS (additional clarity and precision)

Solution 2 (Cheese)

Notice that for any case where the closed loop does not connect from the top side of the ones and bottom side of the ones, there are two of these cases. A cheese solution can be found from this; noting that B and C are the only two options to each other, and, being two apart, with people likely to forget this case, $\boxed{\textbf{(C) }146}$ is likely to be the correct answer. Cheese solution done by juwushu.

Solution 3 (Observation)

We have $2$ cases where the loop does not go through the middle.

If the loop goes through the middle, we must have a full column on $(0,8),(0,7),(1,8),(1,7).$ Then we have $6,5,5,4$ empty middle squares. For each one we can have one on top or one on bottom, so $2^6+2^5+2^5+2^4=144.$ Notice that for each case of fixed toothpicks, there is only one way to form the loop. Then we just add $2+144=\boxed{\textbf{(C) } 146.}$

~nevergonnagiveup

Video Solution by Power Solve

https://www.youtube.com/watch?v=FRNbJ5wIGRo

Video Solution By SpreadTheMathLove

https://www.youtube.com/watch?v=huMQ9J7rIj0&t=77s

Video solution by TheNeuralMathAcademy

https://www.youtube.com/watch?v=4b_YLnyegtw&t=5850s

See Also

2024 AMC 10A (Problems • Answer Key • Resources)
Preceded by
2023 AMC 10B Problems 		Followed by
2024 AMC 10B Problems
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. AMC Logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2024_AMC_10A_Problems/Problem_25&oldid=258671"