Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2024 AMC 8 Problems/Problem 6"

m (→‎Video Solution 1 (Detailed Explanation) 🚀⚡📊)
m (→‎Problem)
 
(3 intermediate revisions by 2 users not shown)
Line 1: Line 1:
−
==Problem==
+
==Problem 6.0==
  
 
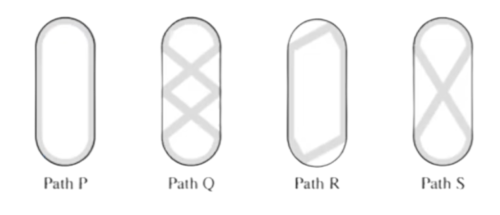
Sergai skated around an ice rink, gliding along different paths. The gray lines in the figures below show four of the paths labeled P, Q, R, and S. What is the sorted order of the four paths from shortest to longest?
 
Sergai skated around an ice rink, gliding along different paths. The gray lines in the figures below show four of the paths labeled P, Q, R, and S. What is the sorted order of the four paths from shortest to longest?
Line 33: Line 33:
 
~MrThinker
 
~MrThinker
  
−
==Video by MathTalks==
+
==Solution 3 (Indepth version of solution 1)==
 +
 
 +
We can compare paths that look similar, <math>P</math> with <math>R</math> and <math>Q</math> with <math>S</math>.
 +
 
 +
<math>R</math> is shorter than <math>P</math> because it replaces curved lines in <math>P</math> with straight lines, and straight lines are always the shortest distance between two points.
 +
 
 +
The two straight lines in <math>S</math> can be seen as paths going diagonally straight across the rink, and the straight lines in <math>Q</math> can be seen as initially going diagonally across the rink, before taking a short detour and then finishing its path. Since a straight line between two points is shorter than zig-zagging lines, path <math>S</math> is shorter than path <math>Q</math>.
 +
 
 +
The only difference between path <math>P</math> and path <math>S</math> is the straight lines, with <math>P</math> going up and down while <math>S</math> goes diagonally. A right triangle can be drawn from a line from <math>P</math> and a line from <math>S</math>. We can see that the straight lines in <math>P</math> act as the leg of the right triangle while the hypotenuse is the straight lines from <math>S</math>. The legs of a right triangle are always less than the hypotenuse, so <math>P</math> is shorter than <math>S</math>.
 +
 
 +
Putting together these inequality statements, the answer is <math>\boxed{\textbf{(D)}~R, P, S, Q}</math>.
 +
 
 +
~Sandcanyon
 +
 
 +
==Video by MathTalks 😉==
  
 
https://www.youtube.com/embed/9GVWXv9Pg1E?si=VYnjDovfhvXwQStu
 
https://www.youtube.com/embed/9GVWXv9Pg1E?si=VYnjDovfhvXwQStu
  
 
~rc1219
 
~rc1219
−
 
−
 
  
 
== Video Solution 1 (Detailed Explanation) 🚀⚡📊 ==
 
== Video Solution 1 (Detailed Explanation) 🚀⚡📊 ==

Latest revision as of 10:16, 31 July 2025

Problem 6.0

Sergai skated around an ice rink, gliding along different paths. The gray lines in the figures below show four of the paths labeled P, Q, R, and S. What is the sorted order of the four paths from shortest to longest?

2024 AMC 8-Problem 6.png

$\textbf{(A)}\ P,Q,R,S \qquad \textbf{(B)}\ P,R,S,Q \qquad \textbf{(C)}\ Q,S,P,R \qquad \textbf{(D)}\ R,P,S,Q \qquad \textbf{(E)}\ R,S,P,Q$

Solution 1

You can measure the lengths of the paths until you find a couple of guaranteed true inferred statements as such: $Q$ is greater than $S$, $P$ is greater than $R$, and $R$ and $P$ are the smallest two, therefore the order is $R, P, S, Q.$ Thus we get the answer $\boxed{\textbf{(D)}~R, P, S, Q}$.

- U-King


~TabHawaii (minor formatting edits)

Solution 2 (Intuitive)

Obviously Path Q is the longest path, followed by Path S.

So, it is down to Paths P and R.

Notice that curved lines are always longer than the straight ones that meet their endpoints, therefore Path P is longer than Path R.

Thus, the order from shortest to longest is $\boxed{\textbf{(D) } \text{R, P, S, Q}}$.

~MrThinker

Solution 3 (Indepth version of solution 1)

We can compare paths that look similar, $P$ with $R$ and $Q$ with $S$.

$R$ is shorter than $P$ because it replaces curved lines in $P$ with straight lines, and straight lines are always the shortest distance between two points.

The two straight lines in $S$ can be seen as paths going diagonally straight across the rink, and the straight lines in $Q$ can be seen as initially going diagonally across the rink, before taking a short detour and then finishing its path. Since a straight line between two points is shorter than zig-zagging lines, path $S$ is shorter than path $Q$.

The only difference between path $P$ and path $S$ is the straight lines, with $P$ going up and down while $S$ goes diagonally. A right triangle can be drawn from a line from $P$ and a line from $S$. We can see that the straight lines in $P$ act as the leg of the right triangle while the hypotenuse is the straight lines from $S$. The legs of a right triangle are always less than the hypotenuse, so $P$ is shorter than $S$.

Putting together these inequality statements, the answer is $\boxed{\textbf{(D)}~R, P, S, Q}$.

~Sandcanyon

Video by MathTalks 😉

https://www.youtube.com/embed/9GVWXv9Pg1E?si=VYnjDovfhvXwQStu

~rc1219

Video Solution 1 (Detailed Explanation) 🚀⚡📊

Youtube Link ⬇️

https://youtu.be/_mMSxc7vXlg

~ ChillGuyDoesMath :)

Video Solution by Central Valley Math Circle(Goes through the full thought process)

https://youtu.be/zCFJ5pKKFXo

~mr_mathman

Video Solution by Math-X (First fully understand the problem!!!)

https://youtu.be/BaE00H2SHQM?si=ZedvqIYTDG3D20Rp&t=1301

~Math-X

Video Solution by Power Solve (easy to digest!)

https://www.youtube.com/watch?v=16YYti_pDUg

Video Solution (A Clever Explanation You’ll Get Instantly)

https://youtu.be/5ZIFnqymdDQ?si=MmMWctYfzKIjwfE8&t=553

~hsnacademy

Video Solution 1 by NiuniuMaths (Easy to understand!)

https://www.youtube.com/watch?v=V-xN8Njd_Lc

~NiuniuMaths

Video Solution by Interstigation

https://youtu.be/ktzijuZtDas&t=386

Video Solution by Daily Dose of Math (Certified, Simple, and Logical)

https://youtu.be/WJCwG6olgNU

~Thesmartgreekmathdude

Video Solution by WhyMath

https://youtu.be/mMDp6k_C6MI

See Also

2024 AMC 8 (Problems • Answer Key • Resources)
Preceded by
Problem 5 		Followed by
Problem 7
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AJHSME/AMC 8 Problems and Solutions

These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. AMC Logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2024_AMC_8_Problems/Problem_6&oldid=256190"