Difference between revisions of "2025 USAMO Problems/Problem 4"
m (specifying point P) |
|||
| (2 intermediate revisions by the same user not shown) | |||
| Line 79: | Line 79: | ||
Therefore <math>OC</math> is perpendicular to chord <math>XY</math>, <math>XC=CY</math>. | Therefore <math>OC</math> is perpendicular to chord <math>XY</math>, <math>XC=CY</math>. | ||
[[File:Usamo_2025_problem4.png|thumb|center|600px]] | [[File:Usamo_2025_problem4.png|thumb|center|600px]] | ||
| + | |||
| + | == Solution 7 == | ||
| + | Let the line perpendicular to <math>BC</math> and going through <math>C</math> be line <math>l</math>. Let the midpoint of <math>AF</math> be <math>M</math>, and let the line perpendicular to <math>AF</math> and going through <math>M</math> be line <math>n</math>. Let <math>O</math> be the intersection of <math>l</math> and <math>n</math>, and let <math>D</math> be the intersections of <math>n</math> and <math>AH</math>. | ||
| + | |||
| + | Because <math>AH\parallel l</math> and <math>CF\parallel n</math>, <math>CODH</math> is a parallelogram. From this, we get <math>OC=DH</math>. Looking at triangle <math>\triangle{FAP}</math>, because <math>n\parallel HF</math>, and <math>M</math> is the midpoint of <math>AF</math>, it is clear that <math>D</math> is the midpoint of <math>AH</math>. | ||
| + | |||
| + | Let the intersection of <math>HP</math> and <math>BC</math> be <math>Z</math>. <math>PZ=ZH</math> because <math>P</math> is a reflection of <math>H</math> across <math>BC</math>. | ||
| + | <math>AP=AH+HP=2DH+2PZ</math> | ||
| + | |||
| + | Substituting the equation from earlier, we get | ||
| + | <math>AP=2OC+2PZ</math> | ||
| + | |||
| + | Draw a line perpendicular to <math>OC</math> starting from <math>O</math>. Let the intersection of that line and <math>AP</math> be <math>E</math>. Because <math>BC</math> is perpendicular to <math>OC</math> which is perpendicular to <math>OE</math>, <math>BC\parallel OE</math>. By the same logic, <math>AP\parallel OC</math>. This means <math>OCZE</math> is a parallelogram (specifically a rectangle). Therefore <math>EZ=OC</math>. <math>EP=EZ+PZ</math> and by substituting, we get <math>EP=OC+PZ</math>, and because <math>AP=2OC+2PZ</math>, that means <math>2EP=AP</math>, so <math>E</math> is a midpoint of <math>AP</math>. This means <math>OE</math> is the perpendicular bisector of <math>AP</math>, and because <math>AP</math> is a chord of the circumcircle of <math>\triangle{FAP}</math>, <math>OE</math> goes through the center of the circle. By the same logic, <math>n</math> also goes through the center of the circle, since it is the perpendicular bisector of <math>AF</math>. This means the center of the circle is <math>O</math>, because it is the only point on both <math>OE</math> and <math>n</math>. Because <math>O</math> is on line <math>OC</math> and line <math>OC</math> is perpendicular to line <math>BC</math>, line <math>OC</math> must perpendicularly bisect the chord of circle <math>O</math> containing <math>C</math> that lies on line <math>BC</math> (basically <math>OC</math> must perpendicularly bisect <math>XY</math>). This means <math>C</math> is the midpoint of <math>XY</math>. | ||
| + | |||
| + | -Nolan Lin | ||
| + | [[File:USAMO4diagram.png|thumb|center|600px]] | ||
Latest revision as of 20:32, 7 August 2025
- The following problem is from both the 2025 USAMO #4 and 2025 USAJMO #5, so both problems redirect to this page.
Contents
Problem
Let ![]() be the orthocenter of acute triangle
be the orthocenter of acute triangle ![]() , let
, let ![]() be the foot of the altitude from
be the foot of the altitude from ![]() to
to ![]() , and let
, and let ![]() be the reflection of
be the reflection of ![]() across
across ![]() . Suppose that the circumcircle of triangle
. Suppose that the circumcircle of triangle ![]() intersects line
intersects line ![]() at two distinct points
at two distinct points ![]() and
and ![]() . Prove that
. Prove that ![]() is the midpoint of
is the midpoint of ![]() .
.
Solution 1
Let AP intersects BC at D. Extend FC to the point E on the circumcircle ![]() of
of ![]() . Since
. Since ![]() is the orthocenter of
is the orthocenter of ![]() , we know that
, we know that ![]() or
or ![]() , and
, and ![]() . Next we use the power of H in
. Next we use the power of H in ![]() :
: ![]() . These relations imply that
. These relations imply that ![]() .
.
Hence ![]() are midpoints of
are midpoints of ![]() respectively. By midline theorem,
respectively. By midline theorem, ![]() . Since
. Since ![]() , we have
, we have ![]() . This implies that
. This implies that ![]() . Consequently,
. Consequently, ![]() is the diameter of
is the diameter of ![]() . Let
. Let ![]() be the midpoint of
be the midpoint of ![]() which is also the center of
which is also the center of ![]() .
. ![]() are midpoints of
are midpoints of ![]() respectively. By the midline theorem again, we have
respectively. By the midline theorem again, we have ![]() , consequently,
, consequently, ![]() . This implies that
. This implies that ![]() is the perpendicular bisector of the chord
is the perpendicular bisector of the chord ![]() hence
hence ![]() is the midpoint of
is the midpoint of ![]() . ~ Dr. Shi davincimath.com
. ~ Dr. Shi davincimath.com
Solution 2
Denote ![]() as the center of
as the center of ![]() ,
, ![]() as the center of
as the center of ![]() ,
, ![]() as the midpoint of
as the midpoint of ![]() ,
, ![]() as the midpoint of
as the midpoint of ![]() , and
, and ![]() as the midpoint of
as the midpoint of ![]() . It suffices to show that
. It suffices to show that ![]() .
.
Claim: ![]() is cyclic.
is cyclic.
Proof: Since ![]() and
and ![]() , KM is a midline of
, KM is a midline of ![]() and
and ![]() .
. ![]() as well since
as well since ![]() , so
, so ![]() lies on
lies on ![]() .
Next, note that
.
Next, note that ![]() lies on
lies on ![]() , so the perpendicular bisector of
, so the perpendicular bisector of ![]() through
through ![]() passes through
passes through ![]() . In other words,
. In other words, ![]() , and
, and ![]() are collinear. Since
are collinear. Since ![]() and
and ![]() are both perpendicular to
are both perpendicular to ![]() , it follows that they are parallel.
Since
, it follows that they are parallel.
Since ![]() and
and ![]() , then
, then ![]() .
Finally, we have that
.
Finally, we have that ![]() and thus
and thus ![]() is cyclic. It follows that
is cyclic. It follows that ![]() , so
, so ![]() , as desired.
, as desired.
-mop
Solution 3
Connect ![]() and have
and have ![]() intersect
intersect ![]() at
at ![]() . Also extend
. Also extend ![]() past point
past point ![]() and have it intersect with the circle at point
and have it intersect with the circle at point ![]() .
.
Since ![]() is the reflection of
is the reflection of ![]() over
over ![]() , we know that
, we know that ![]() . Since
. Since ![]() is the orthocenter, we can draw the altitude and tell that
is the orthocenter, we can draw the altitude and tell that ![]() ,
, ![]() , and
, and ![]() are collinear.
We know
are collinear.
We know ![]() and
and ![]() , so
, so ![]() by AA, so
by AA, so ![]() .
.
![]() and
and ![]() . From this, we can tell that
. From this, we can tell that ![]() . Therefore,
. Therefore, ![]() and
and ![]() .
.
If we connect ![]() , we can tell that that
, we can tell that that ![]() due to
due to ![]() being the reflection of
being the reflection of ![]() and
and ![]() being perpendicular to
being perpendicular to ![]() , so
, so ![]() . In addition,
. In addition, ![]() . Also,
. Also, ![]() because they are vertical angles.
because they are vertical angles.
So, ![]() because of SAA. From this we can conclude that
because of SAA. From this we can conclude that ![]() , so
, so ![]() is the midpoint of
is the midpoint of ![]() .
.
Solution 4
Let ![]() be the foot of the altitude from
be the foot of the altitude from ![]() to
to ![]() By Power of a Point, we have
By Power of a Point, we have
![]() and
and
![]() Adding, we get
Adding, we get
![]() It is well known that the reflection of
It is well known that the reflection of ![]() over
over ![]() which we denote by
which we denote by ![]() lies on
lies on ![]() Then, let
Then, let ![]() We have
We have
![]() Thus,
Thus, ![]() and since
and since ![]() we have
we have ![]() Hence,
Hence, ![]() is the midpoint of
is the midpoint of ![]() ~TThB0501
~TThB0501
Solution 5
Let Q be the antipode of B. Claim — AHQC is a parallelogram, and AP CQ is an isosceles trapezoid.
Proof. As AH ⊥ BC ⊥ CQ and CF ⊥ AB ⊥ AQ. Let M be the midpoint of QC.
Claim — Point M is the circumcenter of triangle AFP.
Proof. It’s clear that MA = MP from the isosceles trapezoid.
As for MA = MF, let N denote the midpoint of AF; then MN is a midline of the parallelogram, so MN ⊥ AF. Since CM ⊥ BC and M is the center of (AF P), it follows CX = CY .
Video Solution - A 2-minute proof
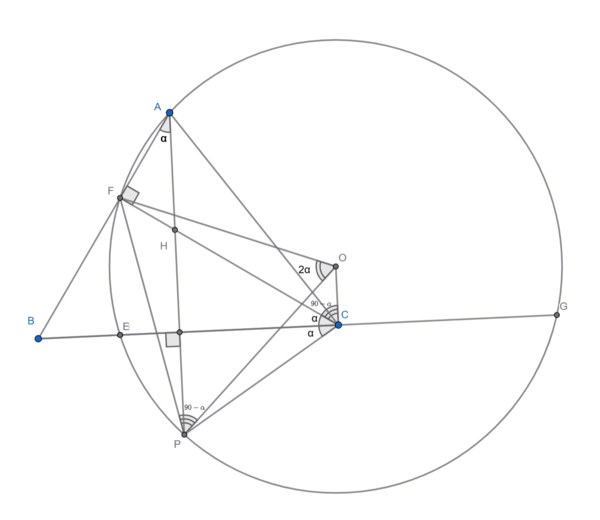
Solution 6
Quick angle chasing gives ![]() .
Let
.
Let ![]() be the circumcenter of
be the circumcenter of ![]() .
.
Thus ![]() (because O and A lie on the same side of segment
(because O and A lie on the same side of segment ![]() ).
).
As ![]() , the quadrilateral FOCP is cyclic.
, the quadrilateral FOCP is cyclic.
Observe that ![]() , so
, so ![]() .
.
From the properties of cyclic quadrilaterals, ![]()
Thus ![]() .
Therefore
.
Therefore ![]() is perpendicular to chord
is perpendicular to chord ![]() ,
, ![]() .
.
Solution 7
Let the line perpendicular to ![]() and going through
and going through ![]() be line
be line ![]() . Let the midpoint of
. Let the midpoint of ![]() be
be ![]() , and let the line perpendicular to
, and let the line perpendicular to ![]() and going through
and going through ![]() be line
be line ![]() . Let
. Let ![]() be the intersection of
be the intersection of ![]() and
and ![]() , and let
, and let ![]() be the intersections of
be the intersections of ![]() and
and ![]() .
.
Because ![]() and
and ![]() ,
, ![]() is a parallelogram. From this, we get
is a parallelogram. From this, we get ![]() . Looking at triangle
. Looking at triangle ![]() , because
, because ![]() , and
, and ![]() is the midpoint of
is the midpoint of ![]() , it is clear that
, it is clear that ![]() is the midpoint of
is the midpoint of ![]() .
.
Let the intersection of ![]() and
and ![]() be
be ![]() .
. ![]() because
because ![]() is a reflection of
is a reflection of ![]() across
across ![]() .
.
![]()
Substituting the equation from earlier, we get
![]()
Draw a line perpendicular to ![]() starting from
starting from ![]() . Let the intersection of that line and
. Let the intersection of that line and ![]() be
be ![]() . Because
. Because ![]() is perpendicular to
is perpendicular to ![]() which is perpendicular to
which is perpendicular to ![]() ,
, ![]() . By the same logic,
. By the same logic, ![]() . This means
. This means ![]() is a parallelogram (specifically a rectangle). Therefore
is a parallelogram (specifically a rectangle). Therefore ![]() .
. ![]() and by substituting, we get
and by substituting, we get ![]() , and because
, and because ![]() , that means
, that means ![]() , so
, so ![]() is a midpoint of
is a midpoint of ![]() . This means
. This means ![]() is the perpendicular bisector of
is the perpendicular bisector of ![]() , and because
, and because ![]() is a chord of the circumcircle of
is a chord of the circumcircle of ![]() ,
, ![]() goes through the center of the circle. By the same logic,
goes through the center of the circle. By the same logic, ![]() also goes through the center of the circle, since it is the perpendicular bisector of
also goes through the center of the circle, since it is the perpendicular bisector of ![]() . This means the center of the circle is
. This means the center of the circle is ![]() , because it is the only point on both
, because it is the only point on both ![]() and
and ![]() . Because
. Because ![]() is on line
is on line ![]() and line
and line ![]() is perpendicular to line
is perpendicular to line ![]() , line
, line ![]() must perpendicularly bisect the chord of circle
must perpendicularly bisect the chord of circle ![]() containing
containing ![]() that lies on line
that lies on line ![]() (basically
(basically ![]() must perpendicularly bisect
must perpendicularly bisect ![]() ). This means
). This means ![]() is the midpoint of
is the midpoint of ![]() .
.
-Nolan Lin