Difference between revisions of "2024 AMC 12A Problems/Problem 18"

Latest revision as of 07:17, 13 August 2025

Problem

On top of a rectangular card with sides of length $1$ and $2+\sqrt{3}$ , an identical card is placed so that two of their diagonals line up, as shown ( $\overline{AC}$ , in this case).

$[asy] defaultpen(fontsize(12)+0.85); size(150); real h=2.25; pair C=origin,B=(0,h),A=(1,h),D=(1,0),Dp=reflect(A,C)*D,Bp=reflect(A,C)*B; pair L=extension(A,Dp,B,C),R=extension(Bp,C,A,D); draw(L--B--A--Dp--C--Bp--A); draw(C--D--R); draw(L--C^^R--A,dashed+0.6); draw(A--C,black+0.6); dot("$C$",C,2*dir(C-R)); dot("$A$",A,1.5*dir(A-L)); dot("$B$",B,dir(B-R)); [/asy]$

Continue the process, adding a third card to the second, and so on, lining up successive diagonals after rotating clockwise. In total, how many cards must be used until a vertex of a new card lands exactly on the vertex labeled $B$ in the figure?

$\textbf{(A) }6\qquad\textbf{(B) }8\qquad\textbf{(C) }10\qquad\textbf{(D) }12\qquad\textbf{(E) }\text{No new vertex will land on }B.$

Solution 1

Let the midpoint of $AC$ be $P$ .

We see that no matter how many moves we do, $P$ stays where it is.

Now we can find the angle of rotation ( $\angle APB$ ) per move with the following steps:

$AP^2=(\frac{1}{2})^2+(1+\frac{\sqrt{3}}{2})^2=2+\sqrt{3}$ $1^2=AP^2+AP^2-2(AP)(AP)\cos\angle APB$ $1=2(2+\sqrt{3})(1-\cos\angle APB)$ $\cos\angle APB=\frac{3+2\sqrt{3}}{4+2\sqrt{3}}$ $\cos\angle APB=\frac{3+2\sqrt{3}}{4+2\sqrt{3}}\cdot\frac{4-2\sqrt{3}}{4-2\sqrt{3}}$ $\cos\angle APB=\frac{2\sqrt{3}}{4}=\frac{\sqrt{3}}{2}$ $\angle APB=30^\circ$ Since Vertex $C$ is the closest one and $\angle BPC=360-180-30=150$

Vertex C will land on Vertex B when $\frac{150}{30}+1=\fbox{(A) 6}$ cards are placed.

(someone insert diagram maybe)

~lptoggled, minor Latex edits by eevee9406

Solution 2

Let AC intersect BD at O,

We want to find $\angle AOB$

Since $tan(75^\circ) = 2+ \sqrt{3} =\frac{AD}{AB}$ , $\angle CBD = \angle BCA = 15^\circ$ $\angle AOB = \angle CBD + \angle BCA =30^\circ$ So each time we rotate BD to AC for $30^\circ$ , and we need to rotate $180^\circ / 30^\circ = 6$ times to overlap a point with B

Therefore, the answer is $\fbox{\textbf{(A) } 6}$

Note: If you don't remember $tan(75^\circ)$

$tan(75^\circ) = \frac{tan(45^\circ) + tan(30^\circ)}{ 1 - tan(45^\circ)\cdot tan(30^\circ)}$

$= \frac{1 + \frac{1}{\sqrt{3}}}{1 - 1 \cdot \frac{1}{\sqrt{3}}}$

$= \frac{(\sqrt{3}+1)^2 }{ (\sqrt{3})^2-1} = 2+ \sqrt{3}$

~luckuso

Solution 3 (Inscribing in Circle)

By the Pythagorean Theorem, $AC = \sqrt{(2 + \sqrt{3})^2 + 1} = \sqrt{8 + 4\sqrt{3}}$ . So we have $\arcsin \angle BCA = \frac{1}{\sqrt{8 + 4\sqrt{3}}} = \frac{1}{\sqrt{(\sqrt{6} + \sqrt{2})^2}} = \frac{\sqrt{6} - \sqrt{2}}{4}.$

We note that $\sin 15^\circ = \cos 75^\circ = \cos(30^\circ + 45^\circ) = \cos30^\circ \cos45^\circ - \sin45^\circ \sin30^\circ = \frac{\sqrt{6} - \sqrt{2}}{4}.$

Therefore, $\angle BCA = 15^\circ.$

Call the rotated rectangle given in the problem's diagram $AB'CD.$ Since $\angle ACB' = \angle BCA = 15^\circ,$ we have $\angle BCB' = 30^\circ.$ So the angle formed between $B$ and $B'$ is $30^\circ \cdot 2 = 60^\circ$ .

In general, when the rectangle is rotated, the angle formed between the left vertex of the original rectangle and the right vertex of the new rectangle is $60^\circ.$ So we can inscribe the rectangles in a circle with $2 \cdot 360/60 = 12$ equally spaced points, and the rotated rectangles will have vertices on these points. $[asy] size(150); defaultpen(fontsize(10pt)); pair O = (0,0); pair[] pts; for (int i = 0; i < 12; ++i) { pts[i] = dir(30 * i); } fill(pts[9]--pts[10]--pts[3]--pts[4]--cycle, paleblue); fill(pts[8]--pts[9]--pts[2]--pts[3]--cycle, palegreen); fill(pts[7]--pts[8]--pts[1]--pts[2]--cycle, palered); draw(Circle(O,1)); draw(O--pts[4], blue+1.5); draw(O--pts[2], blue+1.5); for (int i = 0; i < 12; ++i) { dot(pts[i], black + 3); } dot(O, black + 3); label("$O$", O, SW); label("$B$", pts[4], dir(30 * 4)); label("$A$", pts[3], dir(30 * 3)); label("$B'$", pts[2], dir(30 * 2)); label("$C$", pts[9], dir(30 * 9)); label("$D$", pts[8], dir(30 * 8)); real r = 0.2; draw(arc(O, r, 120, 60), red+1.5); label("$60^\circ$", O + r*dir(90) + (0,0.05), red); [/asy]$

We get the equation $P = 2(R + 1),$ where $R$ is the number of rectangles used and $P$ is the number of points used on the circle for those rectangles (for example, 1 rectangle uses $4$ points, $2$ rectangles use $6$ , etc). The vertex will land on $B$ after we have used all $12$ points on the circle plus the additional $2$ points we get from creating a new rotated rectangle, so $P = 12 + 2 = 14.$ Then $R = \boxed{\textbf{(A) }6}$ .

~grogg007

Solution 4(In case you have no time and that's what I did)

$\tan{15}=\frac{\sin{15}}{\cos{15}}=\frac{1}{2+\sqrt3}$ and it eliminates all options except $6$ and $12$ . After one rotation it has turned $30^{\circ}$ , so to satisfy the problem, divide $\frac{180}{30}$ and get $\boxed{\textbf{A. }6}$ .

Solution 4.5

Memorize that in a 15-75-90 right triangle, the ratios of the side lengths are $1$ , $2+\sqrt3$ , and $\sqrt2+\sqrt6$ . So, we have that the diagonal of the rectangle forms a 15 degree angle. Drawing it out we see the answer is $\boxed{\textbf{(A) }6}$ , and this makes sense because 15 times 6 is 90, thus rotating a vertex back to B.

Solution 5 (the simplest solution ever)

Look at the picture and draw the next one and continue draw down the line and then when you first hit B, count how many rectangles you’ve drawn (excluding the first which hasn’t been rotated), and you should get $\boxed{\textbf{(A) or 6}}$ as the answer.

~EaZ_Shadow

Solution 6

Process is the rotation around the center of the card point $O$ at the angle $\alpha = \angle AOB.$ $AO = BO = R, BD^2 = 4R^2 = AB^2 + AD^2 = 4 \cdot (2+\sqrt{3}).$ By applying the Law of Cosines, we get $2R^2 (1-\cos \alpha) = AB^2 \implies \cos \alpha = \frac {\sqrt{3}}{2} \implies$ $\alpha = 30^\circ \implies \boxed{\textbf{(A) or 6}}.$ vladimir.shelomovskii@gmail.com, vvsss

Solution 7 (No Trig needed)

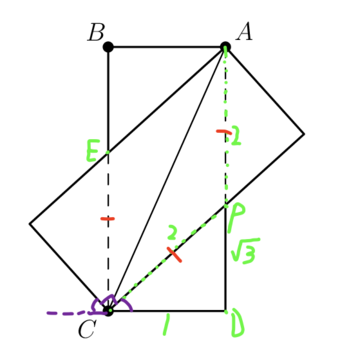
Let E and P be the intersection points, by symmetry axis of $AC$ (since two rectangles are identical), we get:

$CP = CE = CA$

Now assume there exists a point $F$ on $AD$ , where $FD = \sqrt{3}$

Thus:

$AF = (2 + \sqrt{3}) - \sqrt{3} = 2$

Connecting $CF$ , we see that:

$CF = 2$

So F must collide with P, and triangle $PCD$ is a $30^\circ$ - $60^\circ$ - $90^\circ$ triangle, so:

$\angle PCD = 60^\circ$ and external angle would be $30^\circ$ $\implies \boxed{\textbf{(A) or 6}}.$

~D3rrr

Solution 8 (Similar to Solution 1)

Let the vertex of the second rectangular card closest to $C$ be $E$ and the unnamed vertex of the first card be $F$ .

First, notice how the second rectangular card is a reflection of the first rectangular card about $BC$ rotated about $C$ . This means that the diagonal $AC$ from the second rectangular card would have been rotated an angle $2\angle BCA$ clockwise. This also means that side $EC$ would have also been rotated an angle $2\angle BCA$ clockwise, so the angle external to $\angle FCE$ would equal $2\angle BCA$ . When this process is repeated, a regular polygon is formed with half the number of sides of the polygon being the answer.

To find $2\angle BCA$ , we can reflect triangle $ABC$ about $BC$ to form an isosceles triangle. Then

$CA^2=1+(2+\sqrt{3})^2=8+4\sqrt{3}$

By law of cosine:

$(2(1))^2=CA+CA-2(CA)(CA)(\cos (2\angle BCA))$ $4=(2CA^2)(1-\cos (2\angle BCA))$ $4=(2(8+4\sqrt{3})(1-\cos (2\angle BCA))$ $\frac{1}{4+2\sqrt{3}}=1-\cos (2\angle BCA)$ $\frac{3+2\sqrt{3}}{4+2\sqrt{3}}=\cos (2\angle BCA)$

Simplifying:

$\frac{3+2\sqrt{3}}{4+2\sqrt{3}}*\frac{4-2\sqrt{3}}{4-2\sqrt{3}}=\cos (2\angle BCA)$ $\frac{2\sqrt{3}}{4}=\cos (2\angle BCA)$ $\cos (2\angle BCA)=\frac{\sqrt{3}}{2}$ $2\angle BCA = 30^\circ$

The resulting polygon from repeating the process would have $\frac{360}{30}=12$ sides and $\frac{12}{2}=\fbox{(A) 6}$ cards would have to have been placed.

~SandCanyon

2024 AMC 12A (Problems • Answer Key • Resources)
Preceded by Problem 17	Followed by Problem 19
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

Page

Toolbox

Search