Difference between revisions of "2018 AIME I Problems/Problem 8"
(→Solution 1) |
(Undo revision 257526 by Starblaster124 (talk)) (Tag: Undo) |
||
| (10 intermediate revisions by 2 users not shown) | |||
| Line 7: | Line 7: | ||
==Video Solution by Walt S== | ==Video Solution by Walt S== | ||
https://www.youtube.com/watch?v=wGP9bjkdh1M | https://www.youtube.com/watch?v=wGP9bjkdh1M | ||
| + | |||
| + | ==Solution 1== | ||
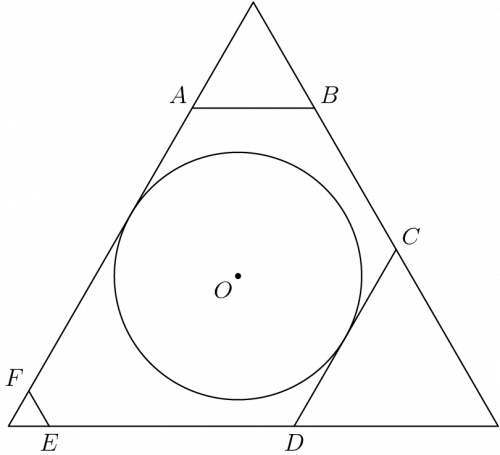
| + | [[image:2018_AIME_I-8.png|center|500px]] | ||
| + | |||
| + | First of all, draw a good diagram! This is always the key to solving any geometry problem. Once you draw it, realize that <math>EF=2, FA=16</math>. Why? Because since the hexagon is equiangular, we can put an equilateral triangle around it, with side length <math>6+8+10=24</math>. Then, if you drew it to scale, notice that the "widest" this circle can be according to <math>AF, CD</math> is <math>7\sqrt{3}</math>. And it will be obvious that the sides won't be inside the circle, so our answer is <math>\boxed{147}</math>. | ||
| + | |||
| + | -expiLnCalc | ||
==Solution 2== | ==Solution 2== | ||
Latest revision as of 20:59, 30 October 2025
Contents
Problem
Let ![]() be an equiangular hexagon such that
be an equiangular hexagon such that ![]() , and
, and ![]() . Denote by
. Denote by ![]() the diameter of the largest circle that fits inside the hexagon. Find
the diameter of the largest circle that fits inside the hexagon. Find ![]() .
.
Video Solution by Punxsutawney Phil
https://www.youtube.com/watch?v=oc-cDRIEzoo
Video Solution by Walt S
https://www.youtube.com/watch?v=wGP9bjkdh1M
Solution 1
First of all, draw a good diagram! This is always the key to solving any geometry problem. Once you draw it, realize that ![]() . Why? Because since the hexagon is equiangular, we can put an equilateral triangle around it, with side length
. Why? Because since the hexagon is equiangular, we can put an equilateral triangle around it, with side length ![]() . Then, if you drew it to scale, notice that the "widest" this circle can be according to
. Then, if you drew it to scale, notice that the "widest" this circle can be according to ![]() is
is ![]() . And it will be obvious that the sides won't be inside the circle, so our answer is
. And it will be obvious that the sides won't be inside the circle, so our answer is ![]() .
.
-expiLnCalc
Solution 2
Like solution 1, draw out the large equilateral triangle with side length ![]() . Let the tangent point of the circle at
. Let the tangent point of the circle at ![]() be G and the tangent point of the circle at
be G and the tangent point of the circle at ![]() be H. Clearly, GH is the diameter of our circle, and is also perpendicular to
be H. Clearly, GH is the diameter of our circle, and is also perpendicular to ![]() and
and ![]() .
.
The equilateral triangle of side length ![]() is similar to our large equilateral triangle of
is similar to our large equilateral triangle of ![]() . And the height of the former equilateral triangle is
. And the height of the former equilateral triangle is ![]() . By our similarity condition,
. By our similarity condition,
![]()
Solving this equation gives ![]() , and
, and ![]()
~novus677
See Also
| 2018 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 7 |
Followed by Problem 9 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. ![]()