Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2002 AMC 12A Problems/Problem 11"

(New page: {{duplicate|2002 AMC 12A #11 and 2002 AMC 10A #12}} == Problem == Mr. Earl E. Bird gets up every day at 8:00 AM to go to work. If he d...)
 
(→‎Solution 4)
 
(23 intermediate revisions by 13 users not shown)
Line 5: Line 5:
 
Mr. Earl E. Bird gets up every day at 8:00 AM to go to work. If he drives at an average speed of 40 miles per hour, he will be late by 3 minutes. If he drives at an average speed of 60 miles per hour, he will be early by 3 minutes. How many miles per hour does Mr. Bird need to drive to get to work exactly on time?
 
Mr. Earl E. Bird gets up every day at 8:00 AM to go to work. If he drives at an average speed of 40 miles per hour, he will be late by 3 minutes. If he drives at an average speed of 60 miles per hour, he will be early by 3 minutes. How many miles per hour does Mr. Bird need to drive to get to work exactly on time?
  
−
<math>\text{(A)}\ 45 \qquad \text{(B)}\ 48 \qquad \text{(C)}\ 50 \qquad \text{(D)}\ 55 \qquad \text{(E)} 58</math>
+
<math>\textbf{(A)}\ 45 \qquad \textbf{(B)}\ 48 \qquad \textbf{(C)}\ 50 \qquad \textbf{(D)}\ 55 \qquad \textbf{(E)}\ 58</math>
  
 
==Solution==
 
==Solution==
 
===Solution 1===
 
===Solution 1===
−
Let the time he needs to get there in be t and the distance he travels be d. From the given equations, we know that <math>d=\left(t+\frac{1}{20}\right)40</math> and <math>d=\left(t-\frac{1}{20}\right)60</math>. Setting the two equal, we have <math>40t+2=60t-2</math> and we find <math>t=\frac{1}{4}</math> of an hour. Substituting t back in, we find <math>d=12</math>. From <math>d=rt</math>, we find that r, and our answer, is <math>\boxed{\text{(B)}\ 48 }</math>.  
+
Let the time he needs to get there in be <math>t</math> and the distance he travels be <math>d</math>. From the given equations, we know that <math>d=\left(t+\frac{1}{20}\right)40</math> and <math>d=\left(t-\frac{1}{20}\right)60</math>. Setting the two equal, we have <math>40t+2=60t-3</math> and we find <math>t=\frac{1}{4}</math> of an hour. Substituting t back in, we find <math>d=12</math>. From <math>d=rt</math>, we find that <math>r</math>, our answer, is <math>\boxed{\textbf{(B) }48 }</math>.
  
 
===Solution 2===
 
===Solution 2===
−
Since either time he arrives at is 3 minutes from the desired time, the answer is merely the [[harmonic mean]] of 40 and 60. The harmonic mean of a and b is <math>\frac{2}{\frac{1}{a}+\frac{1}{b}}=\frac{2ab}{a+b}</math>. In this case, a and b are 40 and 60, so our answer is <math>\frac{4800}{100}=48</math>, so <math>\boxed{\text{(B)}\ 48}</math>.
+
Since either time he arrives at is <math>3</math> minutes from the desired time, the answer is merely the [[harmonic mean]] of 40 and 60.  
 +
Substituting <math>t=\frac ds</math> and dividing both sides by <math>d</math>, we get <math>\frac 2s = \frac 1{40} + \frac 1{60}</math> hence <math>s=\boxed{\textbf{(B) }48}</math>.
 +
 
 +
(Note that this approach would work even if the time by which he is late was different from the time by which he is early in the other case - we would simply take a weighted sum in step two, and hence obtain a weighted harmonic mean in step three.)
  
 
===Solution 3===
 
===Solution 3===
 +
Let x be equal to the total amount of distance he needs to cover. Let y be equal to the amount of time he would travel correctly.
 +
Setting up a system of equations, <math>\frac x{40} -3 = y</math> and <math>\frac x{60} +3 = y</math>
 +
 +
Solving, we get x = 720 and y = 15.
 +
 +
We divide x by y to get the average speed, <math>\frac {720}{15} = 48</math>. Therefore, the answer is <math>\boxed{\textbf{(B) }48}</math>.
 +
 +
~MathKatana
 +
 +
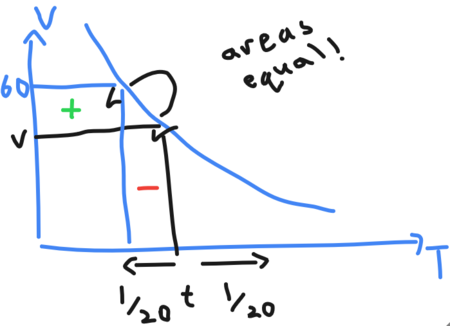
===Solution 4===
 +
Let <math>v</math> be Mr Bird's speed in miles per hour and <math>t</math> be the desired time in hours. No matter what, the product of Mr Bird's speed and time must always be constant.
 +
 +
[[File:Vtequalsconstant.png|450px]]
  
−
A more general form of the argument in Solution 2, with proof:
+
From the diagram above, <math>(60 - v) \left(t - \frac{1}{20} \right) = \frac{v}{20}</math> and similarly, <math>(v - 40)t = \frac{40}{20} = 2</math>. Expanding, <math>60t - 3 - vt + \frac{v}{20} = \frac{v}{20}</math> and so <math>60t - 3 - (2 + 40t) = 0, t = \frac{1}{4}</math>. Hence <math>v = \frac{2}{1/4} + 40 = 48</math>.
  
−
Let <math>d</math> be the distance to work, and let <math>s</math> be the correct average speed. Then the time needed to get to work is <math>t=\frac ds</math>.
+
== Video Solution ==
 +
https://youtu.be/ZpYOnfqm5Bc
  
−
We know that <math>t+\frac 3{60} = \fracd{40}</math> and <math>t-\frac 3{60} = \frac d{60}</math>. Summing these two equations, we get: <math>2t = \frac d{40} + \frac d{60}</math>.
+
==Video Solution by Daily Dose of Math==
  
−
Substituting <math>t=\frac ds</math> and dividing both sides by <math>d</math>, we get <math>\frac 2s = \frac 1{40} + \frac 1{60}</math>, hence <math>s=\boxed{48}</math>.
+
https://youtu.be/S17zidbQYWo
  
−
(Note that this approach would work even if the time by which he is late was different from the time by which he is early in the other case - we would simply take a weighed sum in step two, and hence obtain a weighed harmonic mean in step three.)
+
~Thesmartgreekmathdude
  
 
==See Also==
 
==See Also==
  
−
{{AMC10 box|year=2002|ab=A|num-b=10|num-a=12}}
+
{{AMC12 box|year=2002|ab=A|num-b=10|num-a=12}}
 
{{AMC10 box|year=2002|ab=A|num-b=11|num-a=13}}
 
{{AMC10 box|year=2002|ab=A|num-b=11|num-a=13}}
  
 
[[Category:Introductory Algebra Problems]]
 
[[Category:Introductory Algebra Problems]]
 +
{{MAA Notice}}

Latest revision as of 02:11, 25 March 2025

The following problem is from both the 2002 AMC 12A #11 and 2002 AMC 10A #12, so both problems redirect to this page.

Problem

Mr. Earl E. Bird gets up every day at 8:00 AM to go to work. If he drives at an average speed of 40 miles per hour, he will be late by 3 minutes. If he drives at an average speed of 60 miles per hour, he will be early by 3 minutes. How many miles per hour does Mr. Bird need to drive to get to work exactly on time?

$\textbf{(A)}\ 45 \qquad \textbf{(B)}\ 48 \qquad \textbf{(C)}\ 50 \qquad \textbf{(D)}\ 55 \qquad \textbf{(E)}\ 58$

Solution

Solution 1

Let the time he needs to get there in be $t$ and the distance he travels be $d$. From the given equations, we know that $d=\left(t+\frac{1}{20}\right)40$ and $d=\left(t-\frac{1}{20}\right)60$. Setting the two equal, we have $40t+2=60t-3$ and we find $t=\frac{1}{4}$ of an hour. Substituting t back in, we find $d=12$. From $d=rt$, we find that $r$, our answer, is $\boxed{\textbf{(B) }48 }$.

Solution 2

Since either time he arrives at is $3$ minutes from the desired time, the answer is merely the harmonic mean of 40 and 60. Substituting $t=\frac ds$ and dividing both sides by $d$, we get $\frac 2s = \frac 1{40} + \frac 1{60}$ hence $s=\boxed{\textbf{(B) }48}$.

(Note that this approach would work even if the time by which he is late was different from the time by which he is early in the other case - we would simply take a weighted sum in step two, and hence obtain a weighted harmonic mean in step three.)

Solution 3

Let x be equal to the total amount of distance he needs to cover. Let y be equal to the amount of time he would travel correctly. Setting up a system of equations, $\frac x{40} -3 = y$ and $\frac x{60} +3 = y$

Solving, we get x = 720 and y = 15.

We divide x by y to get the average speed, $\frac {720}{15} = 48$. Therefore, the answer is $\boxed{\textbf{(B) }48}$.

~MathKatana

Solution 4

Let $v$ be Mr Bird's speed in miles per hour and $t$ be the desired time in hours. No matter what, the product of Mr Bird's speed and time must always be constant.

Vtequalsconstant.png

From the diagram above, $(60 - v) \left(t - \frac{1}{20} \right) = \frac{v}{20}$ and similarly, $(v - 40)t = \frac{40}{20} = 2$. Expanding, $60t - 3 - vt + \frac{v}{20} = \frac{v}{20}$ and so $60t - 3 - (2 + 40t) = 0, t = \frac{1}{4}$. Hence $v = \frac{2}{1/4} + 40 = 48$.

Video Solution

https://youtu.be/ZpYOnfqm5Bc

Video Solution by Daily Dose of Math

https://youtu.be/S17zidbQYWo

~Thesmartgreekmathdude

See Also

2002 AMC 12A (Problems • Answer Key • Resources)
Preceded by
Problem 10 		Followed by
Problem 12
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions
2002 AMC 10A (Problems • Answer Key • Resources)
Preceded by
Problem 11 		Followed by
Problem 13
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. AMC Logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2002_AMC_12A_Problems/Problem_11&oldid=246048"