Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2007 AIME I Problems/Problem 13"

(→‎Solution: add solution)
Line 9: Line 9:
 
|}
 
|}
  
−
== Solution ==
+
== Solution 1==
 
Note first that the intersection is a [[pentagon]].
 
Note first that the intersection is a [[pentagon]].
  
Line 15: Line 15:
  
 
Write the equation of the lines and substitute to find that the other two points of intersection on <math>\overline{BE}</math>, <math>\overline{DE}</math> are <math>(\frac{\pm 3}{2},\frac{\pm 3}{2},\frac{\sqrt{2}}{2})</math>. To find the area of the pentagon, break it up into pieces (an [[isosceles triangle]] on the top, an [[isosceles trapezoid]] on the bottom). Using the [[distance formula]] (<math>\sqrt{a^2 + b^2 + c^2}</math>), it is possible to find that the area of the triangle is <math>\frac{1}{2}bh \Longrightarrow \frac{1}{2} 3\sqrt{2} \cdot \sqrt{\frac 52} = \frac{3\sqrt{5}}{2}</math>. The trapezoid has area <math>\frac{1}{2}h(b_1 + b_2) \Longrightarrow \frac 12\sqrt{\frac 52}(2\sqrt{2} + 3\sqrt{2}) = \frac{5\sqrt{5}}{2}</math>. In total, the area is <math>4\sqrt{5} = \sqrt{80}</math>, and the solution is <math>080</math>.
 
Write the equation of the lines and substitute to find that the other two points of intersection on <math>\overline{BE}</math>, <math>\overline{DE}</math> are <math>(\frac{\pm 3}{2},\frac{\pm 3}{2},\frac{\sqrt{2}}{2})</math>. To find the area of the pentagon, break it up into pieces (an [[isosceles triangle]] on the top, an [[isosceles trapezoid]] on the bottom). Using the [[distance formula]] (<math>\sqrt{a^2 + b^2 + c^2}</math>), it is possible to find that the area of the triangle is <math>\frac{1}{2}bh \Longrightarrow \frac{1}{2} 3\sqrt{2} \cdot \sqrt{\frac 52} = \frac{3\sqrt{5}}{2}</math>. The trapezoid has area <math>\frac{1}{2}h(b_1 + b_2) \Longrightarrow \frac 12\sqrt{\frac 52}(2\sqrt{2} + 3\sqrt{2}) = \frac{5\sqrt{5}}{2}</math>. In total, the area is <math>4\sqrt{5} = \sqrt{80}</math>, and the solution is <math>080</math>.
 +
 +
== Solution 2==
 +
Use the same coordinate system as above, and let the plane determined by <math>\triangle PQR</math> intersect <math>\overline{BE}</math> at <math>X</math> and <math>\overline{DE}</math> at <math>Y</math>. Then the line <math>\overline{XY}</math> is the intersection of the planes determined by <math>\triangle PQR</math> and <math>\triangle BDE</math>.
 +
 +
Note that the plane determined by <math>\triangle BDE</math> has the equation <math>x=y</math>, and <math>\overline{PQ}</math> can be described by <math>x=2(1-t)-t,\ y=t,\ z=t\sqrt{2}</math>. It intersects the plane when <math>2(1-t)-t=t</math>, or <math>t=\frac{1}{2}</math>. This intersection point has <math>z=\frac{\sqrt{2}}{2}</math>. Similarly, the intersection between <math>\overline{PR}</math> and <math>\triangle BDE</math> has <math>z=\frac{\sqrt{2}}{2}</math>. So <math>\overline{XY}</math> lies on the plane <math>z=\frac{\sqrt{2}}{2}</math>, from which we obtain <math>X=\left( \frac{3}{2},\frac{3}{2},\frac{\sqrt{2}}{2}\right)</math> and <math>Y=\left( -\frac{3}{2},-\frac{3}{2},\frac{\sqrt{2}}{2}\right)</math>. The area of the pentagon <math>EXQRY</math> can be computed in the same way as above.
  
 
== See also ==
 
== See also ==

Revision as of 15:19, 24 March 2007

Problem

A square pyramid with base $ABCD$ and vertex $E$ has eight edges of length 4. A plane passes through the midpoints of $AE$, $BC$, and $CD$. The plane's intersection with the pyramid has an area that can be expressed as $\sqrt{p}$. Find $p$.

           AIME I 2007-13.png

Solution 1

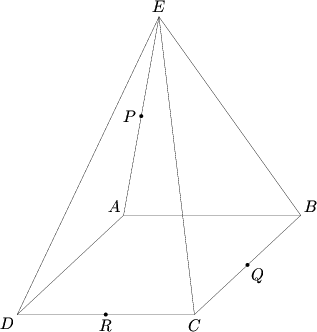
Note first that the intersection is a pentagon.

Use 3D analytical geometry, setting the origin as the center of the square base and the pyramid’s points oriented as shown above. $A(-2,2,0),\ B(2,2,0),\ C(2,-2,0),\ D(-2,-2,0),\ E(0,0,2\sqrt{2})$. Using the coordinates of the three points of intersection ($(-1,1,\sqrt{2}),\ (2,0,0),\ (0,-2,0)$), it is possible to determine the equation of the plane. The equation of a plane resembles $ax + by + cz = d$, and using the points we find that $2a = d \Longrightarrow d = \frac{a}{2}$, $-2b = d \Longrightarrow d = \frac{-b}{2}$, and $-a + b + \sqrt{2}c = d \Longrightarrow -\frac{d}{2} - \frac{d}{2} + \sqrt{2}c = d \Longrightarrow c = d\sqrt{2}$. It is then $x - y + 2\sqrt{2}z = 2$.

Write the equation of the lines and substitute to find that the other two points of intersection on $\overline{BE}$, $\overline{DE}$ are $(\frac{\pm 3}{2},\frac{\pm 3}{2},\frac{\sqrt{2}}{2})$. To find the area of the pentagon, break it up into pieces (an isosceles triangle on the top, an isosceles trapezoid on the bottom). Using the distance formula ($\sqrt{a^2 + b^2 + c^2}$), it is possible to find that the area of the triangle is $\frac{1}{2}bh \Longrightarrow \frac{1}{2} 3\sqrt{2} \cdot \sqrt{\frac 52} = \frac{3\sqrt{5}}{2}$. The trapezoid has area $\frac{1}{2}h(b_1 + b_2) \Longrightarrow \frac 12\sqrt{\frac 52}(2\sqrt{2} + 3\sqrt{2}) = \frac{5\sqrt{5}}{2}$. In total, the area is $4\sqrt{5} = \sqrt{80}$, and the solution is $080$.

Solution 2

Use the same coordinate system as above, and let the plane determined by $\triangle PQR$ intersect $\overline{BE}$ at $X$ and $\overline{DE}$ at $Y$. Then the line $\overline{XY}$ is the intersection of the planes determined by $\triangle PQR$ and $\triangle BDE$.

Note that the plane determined by $\triangle BDE$ has the equation $x=y$, and $\overline{PQ}$ can be described by $x=2(1-t)-t,\ y=t,\ z=t\sqrt{2}$. It intersects the plane when $2(1-t)-t=t$, or $t=\frac{1}{2}$. This intersection point has $z=\frac{\sqrt{2}}{2}$. Similarly, the intersection between $\overline{PR}$ and $\triangle BDE$ has $z=\frac{\sqrt{2}}{2}$. So $\overline{XY}$ lies on the plane $z=\frac{\sqrt{2}}{2}$, from which we obtain $X=\left( \frac{3}{2},\frac{3}{2},\frac{\sqrt{2}}{2}\right)$ and $Y=\left( -\frac{3}{2},-\frac{3}{2},\frac{\sqrt{2}}{2}\right)$. The area of the pentagon $EXQRY$ can be computed in the same way as above.

See also

2007 AIME I (Problems • Answer Key • Resources)
Preceded by
Problem 12 		Followed by
Problem 14
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions
Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2007_AIME_I_Problems/Problem_13&oldid=14168"