Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2009 IMO Problems/Problem 4"

(→‎Problem)
(Added two solutions)
 
Line 5: Line 5:
 
''Authors: Jan Vonk and Peter Vandendriessche, Belgium, and Hojoo Lee, South Korea''
 
''Authors: Jan Vonk and Peter Vandendriessche, Belgium, and Hojoo Lee, South Korea''
  
−
==Solution==
+
==Solution 1==
−
{{solution}}
+
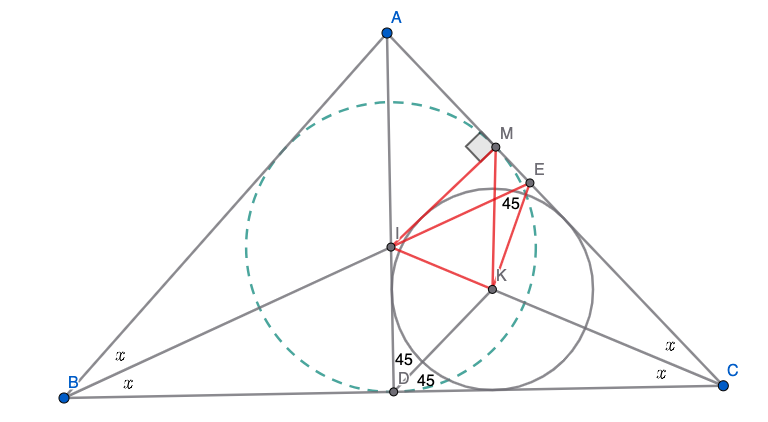
Extend <math>CK</math> to meet <math>BE</math> at <math>I</math>. Then, we can see that <math>I</math> is the incenter of <math>\triangle ABC</math>, so <math>IM=ID</math>, where <math>M</math> is the intersection of the incircle with <math>\overline{AC}</math>.
 +
 
 +
Since <math>CI</math> bisects <math>\angle ACB</math>, we have <math>\triangle IDC \cong \triangle IMC</math>, so <math>\angle IMK = \angle IDK = 45^\circ</math>.
 +
 
 +
From here, there are two possibilities: either <math>M</math> and <math>E</math> coincide or they don't. If <math>M</math> and <math>E</math> coincide, then <math>BM</math> is the median and the altitude from <math>B</math>, so <math>BC = AB</math>, and therefore <math>\triangle ABC</math> is equilateral, so <math>\angle BAC = 60^\circ</math>.
 +
 
 +
Otherwise, we have <math>MIKE</math> is cyclic, and <math>\angle IME = 90^\circ</math>, so <math>IE</math> is the diameter of <math>(MIKE)</math>, so <math>\angle IKE = 90^\circ</math> and <math>\angle KIE = 45^\circ</math>. Also, <math>\angle BIC = 180^\circ - \angle KIE = 135^\circ</math>, so <math>2x = 45^\circ</math>, so <math>\angle CAB = 180^\circ = 4x = 90^\circ</math>, which is the second possible value of <math>\angle CAB</math>.
 +
 
 +
[[File:2009_IMO_P4_(1).png]]
 +
 
 +
==Solution 2==
 +
 
 +
We will be using the trig bash solution given in EGMO.
 +
 
 +
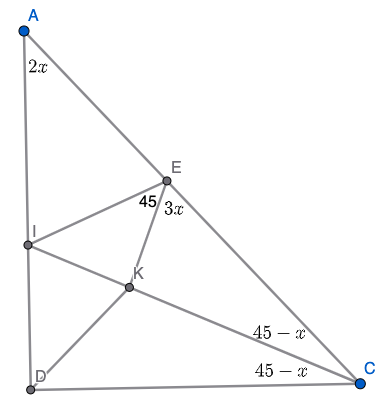
Let <math>I</math> be the incenter, and set <math>\angle DAC = 2x</math> with <math>0 < x < 45</math>. From <math>\angle AIE = \angle DIC</math>, it is easy to compute <cmath>\angle KIE = 90^\circ - 2x, \quad \angle ECI = 45^\circ - x, \quad \angle IEK = 45^\circ, \quad \angle KEC = 3x.</cmath>
 +
 
 +
Then, by LoS, we have <cmath>\dfrac{IK}{KC} = \dfrac{\sin 45^\circ \cdot \frac{EK}{\sin(90^\circ - 2x)}}{\sin(3x) \cdot \frac{EK}{\sin(45^\circ-x)}} = \frac{\sin 45^\circ \sin(45^\circ - x)}{\sin(3x) \sin(90^\circ-2x)}.</cmath>
 +
 
 +
Also, by the angle bisector theorem on <math>\triangle IDC</math>, we get <cmath>\dfrac{IK}{KC} = \dfrac{ID}{DC} = \frac{\sin(45^\circ-x)}{\sin(45^\circ+x)}.</cmath>
 +
 
 +
Equating the above two equations and cancelling <math>\sin(45^\circ-x)</math>, we get <cmath>\sin 45^\circ \sin(45^\circ+x)=\sin 3x \sin(90^\circ - 2x).</cmath>
 +
 
 +
Applying product to sum, we get <cmath>\cos(x)-\cos(90^\circ+x) = \cos(5x-90^\circ)-\cos(90^\circ+x),</cmath>
 +
or simply <math>\cos x = \cos(5x-90^\circ)</math>. Then, applying difference to product, we get <cmath>0 = \cos(5x-90^\circ)-\cos x = 2 \sin(3x-45^\circ) \sin(2x-45^\circ).</cmath>
 +
 
 +
Then, we get two cases: <math>\sin(3x-45^\circ) = 0</math> or <math>\sin(2x-45^\circ) = 0</math>. Note that these hold iff the expressions inside the sines are multiples of <math>180^\circ</math>. Using the bound <math>0 < x < 45</math>, we can easily get that the only possible values are <math>x = 15^\circ</math> and <math>x = \frac{45}{2}^\circ</math>, so <math>\angle A = 60^\circ, 90^\circ</math>.
 +
 
 +
[[File:2009_IMO_P4_(2).png]]
  
 
==See Also==
 
==See Also==
  
 
{{IMO box|year=2009|num-b=3|num-a=5}}
 
{{IMO box|year=2009|num-b=3|num-a=5}}

Latest revision as of 02:29, 22 July 2025

Problem

Let $ABC$ be a triangle with $AB=AC$. The angle bisectors of $\angle CAB$ and $\angle ABC$ meet the sides $BC$ and $CA$ at $D$ and $E$, respectively. Let $K$ be the incenter of triangle $ADC$. Suppose that $\angle BEK=45^\circ$. Find all possible values of $\angle CAB$.

Authors: Jan Vonk and Peter Vandendriessche, Belgium, and Hojoo Lee, South Korea

Solution 1

Extend $CK$ to meet $BE$ at $I$. Then, we can see that $I$ is the incenter of $\triangle ABC$, so $IM=ID$, where $M$ is the intersection of the incircle with $\overline{AC}$.

Since $CI$ bisects $\angle ACB$, we have $\triangle IDC \cong \triangle IMC$, so $\angle IMK = \angle IDK = 45^\circ$.

From here, there are two possibilities: either $M$ and $E$ coincide or they don't. If $M$ and $E$ coincide, then $BM$ is the median and the altitude from $B$, so $BC = AB$, and therefore $\triangle ABC$ is equilateral, so $\angle BAC = 60^\circ$.

Otherwise, we have $MIKE$ is cyclic, and $\angle IME = 90^\circ$, so $IE$ is the diameter of $(MIKE)$, so $\angle IKE = 90^\circ$ and $\angle KIE = 45^\circ$. Also, $\angle BIC = 180^\circ - \angle KIE = 135^\circ$, so $2x = 45^\circ$, so $\angle CAB = 180^\circ = 4x = 90^\circ$, which is the second possible value of $\angle CAB$.

2009 IMO P4 (1).png

Solution 2

We will be using the trig bash solution given in EGMO.

Let $I$ be the incenter, and set $\angle DAC = 2x$ with $0 < x < 45$. From $\angle AIE = \angle DIC$, it is easy to compute \[\angle KIE = 90^\circ - 2x, \quad \angle ECI = 45^\circ - x, \quad \angle IEK = 45^\circ, \quad \angle KEC = 3x.\]

Then, by LoS, we have \[\dfrac{IK}{KC} = \dfrac{\sin 45^\circ \cdot \frac{EK}{\sin(90^\circ - 2x)}}{\sin(3x) \cdot \frac{EK}{\sin(45^\circ-x)}} = \frac{\sin 45^\circ \sin(45^\circ - x)}{\sin(3x) \sin(90^\circ-2x)}.\]

Also, by the angle bisector theorem on $\triangle IDC$, we get \[\dfrac{IK}{KC} = \dfrac{ID}{DC} = \frac{\sin(45^\circ-x)}{\sin(45^\circ+x)}.\]

Equating the above two equations and cancelling $\sin(45^\circ-x)$, we get \[\sin 45^\circ \sin(45^\circ+x)=\sin 3x \sin(90^\circ - 2x).\]

Applying product to sum, we get \[\cos(x)-\cos(90^\circ+x) = \cos(5x-90^\circ)-\cos(90^\circ+x),\] or simply $\cos x = \cos(5x-90^\circ)$. Then, applying difference to product, we get \[0 = \cos(5x-90^\circ)-\cos x = 2 \sin(3x-45^\circ) \sin(2x-45^\circ).\]

Then, we get two cases: $\sin(3x-45^\circ) = 0$ or $\sin(2x-45^\circ) = 0$. Note that these hold iff the expressions inside the sines are multiples of $180^\circ$. Using the bound $0 < x < 45$, we can easily get that the only possible values are $x = 15^\circ$ and $x = \frac{45}{2}^\circ$, so $\angle A = 60^\circ, 90^\circ$.

2009 IMO P4 (2).png

See Also

2009 IMO (Problems) • Resources
Preceded by
Problem 3 		1 • 2 • 3 • 4 • 5 • 6 Followed by
Problem 5
All IMO Problems and Solutions
Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2009_IMO_Problems/Problem_4&oldid=254996"