Difference between revisions of "Power of a Point Theorem"
(Formatting) (Tag: Undo) |
(Merge with Power of a point theorem) |
||
| Line 2: | Line 2: | ||
== Statement == | == Statement == | ||
| + | There are three unique cases for this theorem. Each case expresses the relationship between the length of line segments that pass through a common point and touch a circle in at least one point. Can be useful with [[cyclic quadrilaterals]] as well however with a slightly different application. | ||
| − | + | ===Case 1 (Inside the Circle):=== | |
| − | |||
| − | |||
| − | |||
| − | [[ | + | If two chords <math> AB </math> and <math> CD </math> intersect at a point <math> P </math> within a circle, then <math> AP\cdot BP=CP\cdot DP </math> |
| + | |||
| + | <asy> draw(circle((0,0),3)); | ||
| + | dot((-2.82,1)); | ||
| + | label("A",(-3.05,1.25)); | ||
| + | dot((1,2.828)); | ||
| + | label("B",(1.25,3.05)); | ||
| + | draw((-2.82,1)---(1,2.828)); | ||
| + | dot((2.3,-1.926)); | ||
| + | label("C",(2.55,-2.346)); | ||
| + | dot((-2.12,2.123)); | ||
| + | label("D",(-2.37,2.507)); | ||
| + | draw((2.3,-1.926)---(-2.12,2.123)); | ||
| + | dot((-1.556,1.602)); | ||
| + | label("P",(-1.656,1.202)); | ||
| + | </asy> | ||
| + | |||
| + | ===Case 2 (Outside the Circle):=== | ||
| + | |||
| + | =====Classic Configuration===== | ||
| + | |||
| + | Given lines <math> BP </math> and <math> CP </math> originate from two unique points on the [[circumference]] of a circle (<math> B </math> and <math> C </math>), intersect each other at point <math> P </math>, outside the circle, and re-intersect the circle at points <math> A </math> and <math> D </math> respectively, then <math> PA\cdot PB=PD\cdot PC </math> | ||
| + | |||
| + | <asy> draw(circle((0,0),3)); | ||
| + | dot((1.5,2.598)); | ||
| + | label("B",(2,3)); | ||
| + | label("P",(-6,1.6)); | ||
| + | dot((-6,1)); | ||
| + | label("C",(2.55,-2.5)); | ||
| + | dot((2.12,-2.123)); | ||
| + | dot((-2.996,-0.155)); | ||
| + | label("D",(-3.350, -0.6)); | ||
| + | dot((-2.429,1.761)); | ||
| + | label("A",(-2.729,2.061)); | ||
| + | draw((1.5,2.598)---(-6,1)); | ||
| + | draw((2.12,-2.123)---(-6,1)); | ||
| + | </asy> | ||
| + | |||
| + | =====Tangent Line===== | ||
| + | |||
| + | Given Lines <math> AB </math> and <math> AC </math> with <math> AC </math> [[tangent line|tangent]] to the related circle at <math> C </math>, <math> A </math> lies outside the circle, and Line <math> AB </math> intersects the circle between <math> A </math> and <math> B </math> at <math> D </math>, <math> AD\cdot AB=AC^{2} </math> | ||
| + | |||
| + | <asy> draw(circle((0,0),3)); | ||
| + | dot((0,3)); | ||
| + | label("C",(0,3.5)); | ||
| + | dot((-8,3)); | ||
| + | label("A",(-8,3.5)); | ||
| + | dot((2.5,-1.658)); | ||
| + | label("B",(2.8,-1.958)); | ||
| + | draw((0,3)---(-8,3)); | ||
| + | draw((2.5,-1.658)---(-8,3)); | ||
| + | dot((-2.907,0.741)); | ||
| + | label("D",(-3.357,0.421)); | ||
| + | </asy> | ||
| + | |||
| + | ===Case 3 (On the Border/Useless Case):=== | ||
| + | |||
| + | If two chords, <math> AB </math> and <math> AC </math>, have <math> A </math> on the border of the circle, then the same property such that if two lines that intersect and touch a circle, then the product of each of the lines segments is the same. However since the intersection points lies on the border of the circle, one segment of each line is <math> 0 </math> so no matter what, the constant product is <math> 0 </math>. | ||
| + | |||
| + | <asy> draw(circle((0,0),3)); | ||
| + | dot((1,2.828)); | ||
| + | label("A",(1.4,3.028)); | ||
| + | dot((-2.5,-1.658)); | ||
| + | label("B",(-2.8,-1.958)); | ||
| + | dot((2.04,-2.2)); | ||
| + | label("C",(2.34,-2.5)); | ||
| + | draw((1,2.828)---(-2.5,-1.658)); | ||
| + | draw((1,2.828)---(2.04,-2.2)); | ||
| + | </asy> | ||
=== Alternate Formulation === | === Alternate Formulation === | ||
| Line 34: | Line 100: | ||
''Proof.'' We have already proven the theorem for a <math>1</math>-sphere (a circle), so it only remains to prove the theorem for more dimensions. Consider the [[plane]] <math>p</math> containing both of the lines passing through <math>P</math>. The intersection of <math>P</math> and <math>S</math> must be a circle. If we consider the lines and <math>P</math> with respect simply to that circle, then we have reduced our claim to the case of two dimensions, in which we know the theorem holds. | ''Proof.'' We have already proven the theorem for a <math>1</math>-sphere (a circle), so it only remains to prove the theorem for more dimensions. Consider the [[plane]] <math>p</math> containing both of the lines passing through <math>P</math>. The intersection of <math>P</math> and <math>S</math> must be a circle. If we consider the lines and <math>P</math> with respect simply to that circle, then we have reduced our claim to the case of two dimensions, in which we know the theorem holds. | ||
| + | |||
| + | ==Proof== | ||
| + | |||
| + | ===Case 1 (Inside the Circle)=== | ||
| + | |||
| + | Join <math>AD</math> and <math>BC</math>. | ||
| + | |||
| + | In <math>\triangle ADP \; \text{and} \; \triangle CBP</math> | ||
| + | |||
| + | <math>\angle ADC = \angle CBA \hspace{1cm}</math> (Angles subtended by the same segment are equal) | ||
| + | |||
| + | <math>\angle DPA = \angle BPC \hspace{1cm}</math> (Vertically opposite angles) | ||
| + | |||
| + | <math>\therefore \; \triangle ADP \sim \triangle CBP</math> | ||
| + | |||
| + | <math>\implies \frac{AP}{CP} = \frac{DP}{BP} \hspace{1cm}</math> (Corresponding sides of similar triangles are in the same ratio) | ||
| + | |||
| + | <math>\implies AP \cdot BP = DP \cdot CP</math> | ||
| + | |||
| + | <math>\blacksquare</math> | ||
| + | |||
| + | ===Case 2 (Outside the Circle)=== | ||
| + | |||
| + | Join <math>AD</math> and <math>BC</math> | ||
| + | |||
| + | <math>\angle DAB + \angle DCB = 180^{\circ} = \angle PAD + \angle DAB \hspace{1cm}</math> (Why?) | ||
| + | |||
| + | <math>\implies \angle PCB = \angle DCB = \angle PAD</math> | ||
| + | |||
| + | Now, In <math>\triangle PAD \; \text{and} \; \triangle PCB</math> | ||
| + | |||
| + | <math>\angle PAD = \angle PCB \hspace{1cm}</math> (shown above) | ||
| + | |||
| + | <math>\angle APD = \angle CPB \hspace{1cm}</math> (common angle) | ||
| + | |||
| + | <math>\therefore \; \triangle PAD \sim \triangle PCB</math> | ||
| + | |||
| + | <math>\implies \frac{PA}{PC} = \frac{PD}{PB} \hspace{1cm}</math> (Corresponding sides of similar triangles are in the same ratio) | ||
| + | |||
| + | <math>\implies PA \cdot PB = PD \cdot PC</math> | ||
| + | |||
| + | <math>\blacksquare</math> | ||
| + | |||
| + | ===Case 3 (On the Circle Border)=== | ||
| + | |||
| + | Length of a point is zero so no proof needed :) | ||
== Problems == | == Problems == | ||
| Line 51: | Line 163: | ||
* ([[ARML]]) Chords <math>AB</math> and <math>CD</math> of a given circle are [[perpendicular]] to each other and intersect at a right angle at point <math>E</math>. Given that <math>BE=16</math>, <math>DE=4</math>, and <math>AD=5</math>, find <math>CE</math>. | * ([[ARML]]) Chords <math>AB</math> and <math>CD</math> of a given circle are [[perpendicular]] to each other and intersect at a right angle at point <math>E</math>. Given that <math>BE=16</math>, <math>DE=4</math>, and <math>AD=5</math>, find <math>CE</math>. | ||
:[[Power of a Point Theorem/Introductory_Problem_4|Solution]] | :[[Power of a Point Theorem/Introductory_Problem_4|Solution]] | ||
| + | |||
| + | * Let <math>\overline{AB}</math> be a diameter in a circle of radius <math>5\sqrt2.</math> Let <math>\overline{CD}</math> be a chord in the circle that intersects <math>\overline{AB}</math> at a point <math>E</math> such that <math>BE=2\sqrt5</math> and <math>\angle AEC = 45^{\circ}.</math> What is <math>CE^2+DE^2?</math> ([[2020 AMC 12B Problems/Problem 12|Source]]) | ||
=== Intermediate === | === Intermediate === | ||
| Line 62: | Line 176: | ||
* Triangle <math>ABC</math> has <math>BC=20.</math> The incircle of the triangle evenly trisects the median <math>AD.</math> If the area of the triangle is <math>m \sqrt{n}</math> where <math>m</math> and <math>n</math> are integers and <math>n</math> is not divisible by the square of a prime, find <math>m+n.</math> ([[2005 AIME I Problems/Problem 15|Source]]) | * Triangle <math>ABC</math> has <math>BC=20.</math> The incircle of the triangle evenly trisects the median <math>AD.</math> If the area of the triangle is <math>m \sqrt{n}</math> where <math>m</math> and <math>n</math> are integers and <math>n</math> is not divisible by the square of a prime, find <math>m+n.</math> ([[2005 AIME I Problems/Problem 15|Source]]) | ||
| + | |||
| + | * Let <math>ABC</math> be a triangle inscribed in circle <math>\omega</math>. Let the tangents to <math>\omega</math> at <math>B</math> and <math>C</math> intersect at point <math>D</math>, and let <math>\overline{AD}</math> intersect <math>\omega</math> at <math>P</math>. If <math>AB=5</math>, <math>BC=9</math>, and <math>AC=10</math>, <math>AP</math> can be written as the form <math>\frac{m}{n}</math>, where <math>m</math> and <math>n</math> are relatively prime integers. Find <math>m + n</math>. ([[2024 AIME I Problems/Problem 10|Source]]) | ||
=== Olympiad === | === Olympiad === | ||
| − | * | + | * Given circles <math>\omega_1</math> and <math>\omega_2</math> intersecting at points <math>X</math> and <math>Y</math>, let <math>\ell_1</math> be a line through the center of <math>\omega_1</math> intersecting <math>\omega_2</math> at points <math>P</math> and <math>Q</math> and let <math>\ell_2</math> be a line through the center of <math>\omega_2</math> intersecting <math>\omega_1</math> at points <math>R</math> and <math>S</math>. Prove that if <math>P, Q, R</math> and <math>S</math> lie on a circle then the center of this circle lies on line <math>XY</math>. |
| + | |||
| + | ([[2009 USAMO Problems/Problem 1|Source]]) | ||
| + | |||
| + | Let <math>P</math> be a point interior to triangle <math>ABC</math> (with <math>CA \neq CB</math>). The lines <math>AP</math>, <math>BP</math> and <math>CP</math> meet again its circumcircle <math>\Gamma</math> at <math>K</math>, <math>L</math>, respectively <math>M</math>. The tangent line at <math>C</math> to <math>\Gamma</math> meets the line <math>AB</math> at <math>S</math>. Show that from <math>SC = SP</math> follows <math>MK = ML</math>. | ||
| + | |||
| + | ([[2010 IMO Problems/Problem 4|Source]]) | ||
== See Also == | == See Also == | ||
| Line 71: | Line 193: | ||
* [[Geometry]] | * [[Geometry]] | ||
* [[Planar figures]] | * [[Planar figures]] | ||
| − | * [{{SERVER}}/community/c6h2513977 | + | |
| + | === External Links === | ||
| + | * [{{SERVER}}/community/c6h2513977 Handout on AoPS Forums] | ||
[[Category:Geometry]] | [[Category:Geometry]] | ||
[[Category:Theorems]] | [[Category:Theorems]] | ||
{{stub}} | {{stub}} | ||
Latest revision as of 22:56, 22 March 2025
The Power of a Point Theorem is a relationship that holds between the lengths of the line segments formed when two lines intersect a circle and each other.
Contents
Statement
There are three unique cases for this theorem. Each case expresses the relationship between the length of line segments that pass through a common point and touch a circle in at least one point. Can be useful with cyclic quadrilaterals as well however with a slightly different application.
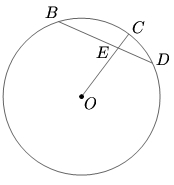
Case 1 (Inside the Circle):
If two chords ![]() and
and ![]() intersect at a point
intersect at a point ![]() within a circle, then
within a circle, then ![]()
![[asy] draw(circle((0,0),3)); dot((-2.82,1)); label("A",(-3.05,1.25)); dot((1,2.828)); label("B",(1.25,3.05)); draw((-2.82,1)---(1,2.828)); dot((2.3,-1.926)); label("C",(2.55,-2.346)); dot((-2.12,2.123)); label("D",(-2.37,2.507)); draw((2.3,-1.926)---(-2.12,2.123)); dot((-1.556,1.602)); label("P",(-1.656,1.202)); [/asy]](http://latex.artofproblemsolving.com/4/3/e/43ea0defa651cb6ea1bff713078ff1db02e4bbd2.png)
Case 2 (Outside the Circle):
Classic Configuration
Given lines ![]() and
and ![]() originate from two unique points on the circumference of a circle (
originate from two unique points on the circumference of a circle (![]() and
and ![]() ), intersect each other at point
), intersect each other at point ![]() , outside the circle, and re-intersect the circle at points
, outside the circle, and re-intersect the circle at points ![]() and
and ![]() respectively, then
respectively, then ![]()
![[asy] draw(circle((0,0),3)); dot((1.5,2.598)); label("B",(2,3)); label("P",(-6,1.6)); dot((-6,1)); label("C",(2.55,-2.5)); dot((2.12,-2.123)); dot((-2.996,-0.155)); label("D",(-3.350, -0.6)); dot((-2.429,1.761)); label("A",(-2.729,2.061)); draw((1.5,2.598)---(-6,1)); draw((2.12,-2.123)---(-6,1)); [/asy]](http://latex.artofproblemsolving.com/a/2/f/a2fef94f077027ff64b91d68eb22d519e074b465.png)
Tangent Line
Given Lines ![]() and
and ![]() with
with ![]() tangent to the related circle at
tangent to the related circle at ![]() ,
, ![]() lies outside the circle, and Line
lies outside the circle, and Line ![]() intersects the circle between
intersects the circle between ![]() and
and ![]() at
at ![]() ,
, ![]()
![[asy] draw(circle((0,0),3)); dot((0,3)); label("C",(0,3.5)); dot((-8,3)); label("A",(-8,3.5)); dot((2.5,-1.658)); label("B",(2.8,-1.958)); draw((0,3)---(-8,3)); draw((2.5,-1.658)---(-8,3)); dot((-2.907,0.741)); label("D",(-3.357,0.421)); [/asy]](http://latex.artofproblemsolving.com/e/f/7/ef75f84250744d84969c0011b8851dd821f71913.png)
Case 3 (On the Border/Useless Case):
If two chords, ![]() and
and ![]() , have
, have ![]() on the border of the circle, then the same property such that if two lines that intersect and touch a circle, then the product of each of the lines segments is the same. However since the intersection points lies on the border of the circle, one segment of each line is
on the border of the circle, then the same property such that if two lines that intersect and touch a circle, then the product of each of the lines segments is the same. However since the intersection points lies on the border of the circle, one segment of each line is ![]() so no matter what, the constant product is
so no matter what, the constant product is ![]() .
.
![[asy] draw(circle((0,0),3)); dot((1,2.828)); label("A",(1.4,3.028)); dot((-2.5,-1.658)); label("B",(-2.8,-1.958)); dot((2.04,-2.2)); label("C",(2.34,-2.5)); draw((1,2.828)---(-2.5,-1.658)); draw((1,2.828)---(2.04,-2.2)); [/asy]](http://latex.artofproblemsolving.com/e/6/c/e6c7739952d55c0acfc3d481d0515b21a6cb9ca9.png)
Alternate Formulation
This alternate formulation is much more compact, convenient, and general.
Consider a circle ![]() and a point
and a point ![]() in the plane where
in the plane where ![]() is not on the circle. Now draw a line through
is not on the circle. Now draw a line through ![]() that intersects the circle in two places. The power of a point theorem says that the product of the length from
that intersects the circle in two places. The power of a point theorem says that the product of the length from ![]() to the first point of intersection and the length from
to the first point of intersection and the length from ![]() to the second point of intersection is constant for any choice of a line through
to the second point of intersection is constant for any choice of a line through ![]() that intersects the circle. This constant is called the power of point
that intersects the circle. This constant is called the power of point ![]() . For example, in the figure below
. For example, in the figure below
![]()
Hint for Proof
Draw extra lines to create similar triangles (Draw ![]() on all three figures. Draw another line as well.)
on all three figures. Draw another line as well.)
Notice how this definition still works if ![]() and
and ![]() coincide (as is the case with
coincide (as is the case with ![]() ). Consider also when
). Consider also when ![]() is inside the circle. The definition still holds in this case.
is inside the circle. The definition still holds in this case.
Notes
One important result of this theorem is that both tangents from any point ![]() outside of a circle to that circle are equal in length.
outside of a circle to that circle are equal in length.
The theorem generalizes to higher dimensions, as follows.
Let ![]() be a point, and let
be a point, and let ![]() be an
be an ![]() -sphere. Let two arbitrary lines passing through
-sphere. Let two arbitrary lines passing through ![]() intersect
intersect ![]() at
at ![]() , respectively. Then
, respectively. Then
![]()
Proof. We have already proven the theorem for a ![]() -sphere (a circle), so it only remains to prove the theorem for more dimensions. Consider the plane
-sphere (a circle), so it only remains to prove the theorem for more dimensions. Consider the plane ![]() containing both of the lines passing through
containing both of the lines passing through ![]() . The intersection of
. The intersection of ![]() and
and ![]() must be a circle. If we consider the lines and
must be a circle. If we consider the lines and ![]() with respect simply to that circle, then we have reduced our claim to the case of two dimensions, in which we know the theorem holds.
with respect simply to that circle, then we have reduced our claim to the case of two dimensions, in which we know the theorem holds.
Proof
Case 1 (Inside the Circle)
Join ![]() and
and ![]() .
.
In ![]()
![]() (Angles subtended by the same segment are equal)
(Angles subtended by the same segment are equal)
![]() (Vertically opposite angles)
(Vertically opposite angles)
![]()
![]() (Corresponding sides of similar triangles are in the same ratio)
(Corresponding sides of similar triangles are in the same ratio)
![]()
![]()
Case 2 (Outside the Circle)
Join ![]() and
and ![]()
![]() (Why?)
(Why?)
![]()
Now, In ![]()
![]() (shown above)
(shown above)
![]() (common angle)
(common angle)
![]()
![]() (Corresponding sides of similar triangles are in the same ratio)
(Corresponding sides of similar triangles are in the same ratio)
![]()
![]()
Case 3 (On the Circle Border)
Length of a point is zero so no proof needed :)
Problems
Introductory
- Find the value of
 in the following diagram:
in the following diagram:
- Find the value of
 in the following diagram:
in the following diagram:
- (ARML) In a circle, chords
 and
and  intersect at
intersect at  . If
. If  and
and  , find the ratio
, find the ratio  .
.
- (ARML) Chords
 and
and  of a given circle are perpendicular to each other and intersect at a right angle at point
of a given circle are perpendicular to each other and intersect at a right angle at point  . Given that
. Given that  ,
,  , and
, and  , find
, find  .
.
- Let
 be a diameter in a circle of radius
be a diameter in a circle of radius  Let
Let  be a chord in the circle that intersects
be a chord in the circle that intersects  at a point
at a point  such that
such that  and
and  What is
What is  (Source)
(Source)
Intermediate
- Two tangents from an external point
 are drawn to a circle and intersect it at
are drawn to a circle and intersect it at  and
and  . A third tangent meets the circle at
. A third tangent meets the circle at  , and the tangents
, and the tangents  and
and  at points
at points  and
and  , respectively (this means that T is on the minor arc
, respectively (this means that T is on the minor arc  ). If
). If  , find the perimeter of
, find the perimeter of  . (Source)
. (Source)
- Square
 of side length
of side length  has a circle inscribed in it. Let
has a circle inscribed in it. Let  be the midpoint of
be the midpoint of  . Find the length of that portion of the segment
. Find the length of that portion of the segment  that lies outside of the circle. (Source)
that lies outside of the circle. (Source)
 is a chord of a circle such that
is a chord of a circle such that  and
and  Let
Let  be the center of the circle. Join
be the center of the circle. Join  and extend
and extend  to cut the circle at
to cut the circle at  Given
Given  find the radius of the circle. (Source)
find the radius of the circle. (Source)
- Triangle
 has
has  The incircle of the triangle evenly trisects the median
The incircle of the triangle evenly trisects the median  If the area of the triangle is
If the area of the triangle is  where
where  and
and  are integers and
are integers and  is not divisible by the square of a prime, find
is not divisible by the square of a prime, find  (Source)
(Source)
- Let
 be a triangle inscribed in circle
be a triangle inscribed in circle  . Let the tangents to
. Let the tangents to  at
at  and
and  intersect at point
intersect at point  , and let
, and let  intersect
intersect  at
at  . If
. If  ,
,  , and
, and  ,
,  can be written as the form
can be written as the form  , where
, where  and
and  are relatively prime integers. Find
are relatively prime integers. Find  . (Source)
. (Source)
Olympiad
- Given circles
 and
and  intersecting at points
intersecting at points  and
and  , let
, let  be a line through the center of
be a line through the center of  intersecting
intersecting  at points
at points  and
and  and let
and let  be a line through the center of
be a line through the center of  intersecting
intersecting  at points
at points  and
and  . Prove that if
. Prove that if  and
and  lie on a circle then the center of this circle lies on line
lie on a circle then the center of this circle lies on line  .
.
(Source)
Let ![]() be a point interior to triangle
be a point interior to triangle ![]() (with
(with ![]() ). The lines
). The lines ![]() ,
, ![]() and
and ![]() meet again its circumcircle
meet again its circumcircle ![]() at
at ![]() ,
, ![]() , respectively
, respectively ![]() . The tangent line at
. The tangent line at ![]() to
to ![]() meets the line
meets the line ![]() at
at ![]() . Show that from
. Show that from ![]() follows
follows ![]() .
.
(Source)
See Also
External Links
This article is a stub. Help us out by expanding it.