Difference between revisions of "2013 CEMC Gauss (Grade 8) Problems/Problem 17"
m |
|||
| Line 1: | Line 1: | ||
== Problem == | == Problem == | ||
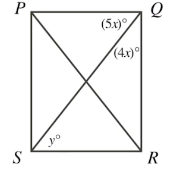
<math>PQRS</math> is a rectangle with diagonals <math>PR</math> and <math>QS</math>, as shown. | <math>PQRS</math> is a rectangle with diagonals <math>PR</math> and <math>QS</math>, as shown. | ||
| − | |||
The value of y is | The value of y is | ||
| Line 15: | Line 14: | ||
\textbf{(E)}\ 60 | \textbf{(E)}\ 60 | ||
</math> | </math> | ||
| + | |||
| + | |||
| + | |||
| + | [[File:2013CEMCGauss8P17diagram.png]] | ||
| + | |||
| + | ~diagram uploaded by [[sharmaguy]] | ||
| + | |||
== Solution 1== | == Solution 1== | ||
The interior angles of a [[rectangle]] are all [[right angle]]s, and the [[acute angle]]s of a [[right triangle]] sum up to <math>90^{\circ}</math>. Thus, we have the following equations: | The interior angles of a [[rectangle]] are all [[right angle]]s, and the [[acute angle]]s of a [[right triangle]] sum up to <math>90^{\circ}</math>. Thus, we have the following equations: | ||
Revision as of 18:29, 17 June 2025
Contents
Problem
![]() is a rectangle with diagonals
is a rectangle with diagonals ![]() and
and ![]() , as shown.
The value of y is
, as shown.
The value of y is
![]()
~diagram uploaded by sharmaguy
Solution 1
The interior angles of a rectangle are all right angles, and the acute angles of a right triangle sum up to ![]() . Thus, we have the following equations:
. Thus, we have the following equations:
![]()
![]()
Solving the first equation for ![]() , we get:
, we get:
![]()
![]()
Plugging ![]() into the second equation, we have:
into the second equation, we have:
![]()
![]()
![]()
~anabel.disher
Solution 2
We can use the above process to find ![]() , and then notice
, and then notice ![]() and
and ![]() would be alternate interior angles. Thus,
would be alternate interior angles. Thus,
![]()
~anabel.disher
Solution 2.5
We can also get to the conclusion that ![]() by using the equations:
by using the equations:
![]()
![]()
![]()
~anabel.disher