Difference between revisions of "Squeeze Theorem"
| Line 5: | Line 5: | ||
==Theorem== | ==Theorem== | ||
| − | Suppose f(x) is between g(x) and h(x) for all x in the neighborhood of S. If g and h approach some common limit L as x approaches S, then \lim_{x\to S}f(x)=L. | + | Suppose <math>f(x)</math> is between <math>g(x)</math> and <math>h(x)</math> for all <math>x</math> in the neighborhood of <math>S</math>. If <math>g</math> and <math>h</math> approach some common limit L as <math>x</math> approaches <math>S</math>, then <math>\lim_{x\to S}f(x)=L</math>. |
==Proof== | ==Proof== | ||
Revision as of 12:09, 7 May 2008
| This is an AoPSWiki Word of the Week for May 4-11 |
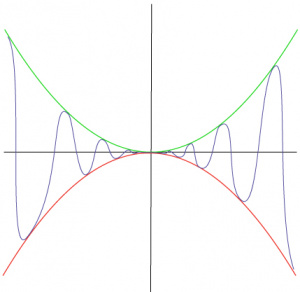
The Squeeze Theorem (also called the Sandwich Theorem or the Squeeze Play Theorem) is a relatively simple theorem that deals with calculus, specifically limits.
Theorem
Suppose 
is between 
and 
for all 
in the neighborhood of 
. If 
and 
approach some common limit L as approaches , then 
.
Proof
If is between and for all in the neighborhood of , then either 
or 
for all in the neighborhood of . Since the second case is basically the first case, we just need to prove the first case.
For all 
, we must prove that there is some 
for which 
.
Now since, 
, there must exist 
such that,
and,
Now let 
. If 
, then
So 
. Now by the definition of a limit, we get .
