Difference between revisions of "2024 AMC 10A Problems/Problem 22"
Cheappotatox (talk | contribs) |
(→Solution 2) |
||
| Line 22: | Line 22: | ||
==Solution 2== | ==Solution 2== | ||
| − | + | Let's start by looking at kite <math>\mathcal K</math>. We can quickly deduce based off of the side lengths that the kite can be split into <math>2</math> <math>30</math>-<math>60</math>-<math>90</math> triangles. Going back to the triangle ABC, focus on side AB. There are <math>4</math> kites, they are all either reflected over the line AB or a line perpendicular to AB, meaning the length of AB can be split up into 4 equal parts. | |
| + | |||
| + | Pick out the bottom-left kite, and we can observe that the kite and the triangle formed by the intersection of the kite and <math>\Delta ABC</math> share a <math>60</math> degree angle. (this was deduced from the <math>30</math>-<math>60</math>-<math>90</math> triangles in the kite) The line AB and the right side of the kite are perpendicular, forming a <math>90</math> degree angle. Because that is also a <math>30</math>-<math>60</math>-<math>90</math> triangle with a hypotenuse of <math>\sqrt3</math>, so we find the length of AB to be <math>4*3/2</math>, which is <math>6</math>. | ||
| + | |||
| + | Then, we can drop an altitude from C to AB. We know that will be equivalent to the sum of the longer side of the kite and the shorter side of the triangle formed by the intersection of the kite and <math>\Delta ABC</math>. (Look at the line formed on the left of C that drops down to AB if you are confused) We already have those values from the <math>30</math>-<math>60</math>-<math>90</math> triangles, so we can just plug it into the triangle area formula, <math>bh/2</math>. We get <math>6*(\sqrt3+\sqrt3/2)/2</math> ==> <math>3*(\sqrt3+\sqrt3/2)</math> ==> <math>3*\sqrt3/2</math> ==> <math>\textbf{(B) }\dfrac92\sqrt3\qquad</math> | ||
| + | |||
| + | ~YTH (Need help with Latex and formatting) | ||
~WIP (Header) | ~WIP (Header) | ||
| − | |||
==See also== | ==See also== | ||
{{AMC10 box|year=2024|ab=A|num-b=21|num-a=23}} | {{AMC10 box|year=2024|ab=A|num-b=21|num-a=23}} | ||
{{MAA Notice}} | {{MAA Notice}} | ||
Revision as of 19:37, 8 November 2024
Contents
Problem
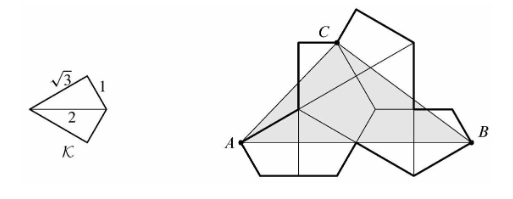
Let ![]() be the kite formed by joining two right triangles with legs
be the kite formed by joining two right triangles with legs ![]() and
and ![]() along a common hypotenuse. Eight copies of
along a common hypotenuse. Eight copies of ![]() are used to form the polygon shown below. What is the area of triangle
are used to form the polygon shown below. What is the area of triangle ![]() ?
?
![]()
Solution 1
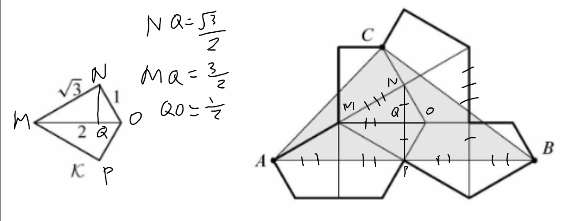
Let ![]() be quadrilateral MNOP. Drawing line MO splits the triangle into
be quadrilateral MNOP. Drawing line MO splits the triangle into ![]() .
Drawing the altitude from N to point Q on line MO, we know NQ is
.
Drawing the altitude from N to point Q on line MO, we know NQ is ![]() , MQ is
, MQ is ![]() , and QO is
, and QO is ![]() .
.
Due to the many similarities present, we can find that AB is ![]() , and the height of
, and the height of ![]() is
is ![]()
AB is ![]() and the height of
and the height of ![]() is
is ![]() .
.
Solving for the area of ![]() gives
gives ![]() which is
which is ![]()
~9897 (latex beginner here)
Solution 2
Let's start by looking at kite ![]() . We can quickly deduce based off of the side lengths that the kite can be split into
. We can quickly deduce based off of the side lengths that the kite can be split into ![]()
![]() -
-![]() -
-![]() triangles. Going back to the triangle ABC, focus on side AB. There are
triangles. Going back to the triangle ABC, focus on side AB. There are ![]() kites, they are all either reflected over the line AB or a line perpendicular to AB, meaning the length of AB can be split up into 4 equal parts.
kites, they are all either reflected over the line AB or a line perpendicular to AB, meaning the length of AB can be split up into 4 equal parts.
Pick out the bottom-left kite, and we can observe that the kite and the triangle formed by the intersection of the kite and ![]() share a
share a ![]() degree angle. (this was deduced from the
degree angle. (this was deduced from the ![]() -
-![]() -
-![]() triangles in the kite) The line AB and the right side of the kite are perpendicular, forming a
triangles in the kite) The line AB and the right side of the kite are perpendicular, forming a ![]() degree angle. Because that is also a
degree angle. Because that is also a ![]() -
-![]() -
-![]() triangle with a hypotenuse of
triangle with a hypotenuse of ![]() , so we find the length of AB to be
, so we find the length of AB to be ![]() , which is
, which is ![]() .
.
Then, we can drop an altitude from C to AB. We know that will be equivalent to the sum of the longer side of the kite and the shorter side of the triangle formed by the intersection of the kite and ![]() . (Look at the line formed on the left of C that drops down to AB if you are confused) We already have those values from the
. (Look at the line formed on the left of C that drops down to AB if you are confused) We already have those values from the ![]() -
-![]() -
-![]() triangles, so we can just plug it into the triangle area formula,
triangles, so we can just plug it into the triangle area formula, ![]() . We get
. We get ![]() ==>
==> ![]() ==>
==> ![]() ==>
==> ![]()
~YTH (Need help with Latex and formatting)
~WIP (Header)
See also
| 2024 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by Problem 21 |
Followed by Problem 23 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. ![]()