Difference between revisions of "Stereographic projection"
Duck master (talk | contribs) (replaced nonsense with content) |
|||
| Line 2: | Line 2: | ||
To stereographically project a point on a sphere to a plane tangent to its south pole, draw the line from the north pole of the sphere to the point in question. The stereographic projection of this point is then the intersection of this line with the plane. As such, the stereographic projection of the north pole will be undefined. | To stereographically project a point on a sphere to a plane tangent to its south pole, draw the line from the north pole of the sphere to the point in question. The stereographic projection of this point is then the intersection of this line with the plane. As such, the stereographic projection of the north pole will be undefined. | ||
| + | |||
| + | ==Moscow Math Olympiad, 1950== | ||
| + | [[File:MMO 1950.png|300px|right]] | ||
| + | A spatial quadrilateral is circumscribed about the sphere. | ||
| + | |||
| + | Prove that the four points of contact lie in one plane. | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
{{stub}}[[Category:Geometry]] | {{stub}}[[Category:Geometry]] | ||
Revision as of 16:48, 2 May 2025
A stereographic projection is a projection from a sphere to a tangent plane. Stereographic projections preserve angles.
To stereographically project a point on a sphere to a plane tangent to its south pole, draw the line from the north pole of the sphere to the point in question. The stereographic projection of this point is then the intersection of this line with the plane. As such, the stereographic projection of the north pole will be undefined.
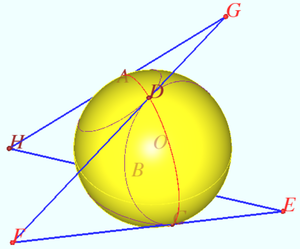
Moscow Math Olympiad, 1950
A spatial quadrilateral is circumscribed about the sphere.
Prove that the four points of contact lie in one plane.
Proof
This article is a stub. Help us out by expanding it.