Difference between revisions of "Sharygin Olympiads, the best"
(→2025 I Problem 1) |
(→2025 II Problem 10 2) |
||
| Line 356: | Line 356: | ||
'''vladimir.shelomovskii@gmail.com, vvsss''' | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | ==2025 II Problem 10 3== | ||
| + | [[File:Tur 2 2025 10 3.png|300px|right]] | ||
| + | Is it possible to take six points <math>A,B,C,D,E,F</math> in general position in space so that triangles <math>\triangle ABC</math> and <math>\triangle DEF</math> are “linked”, but two triangles corresponding to any other partition of these points into two triplets are not? Two triangles in space are “linked” if the contour of one intersects the interior of the other at a single point. (E. Alkin, A. Skopenkov) | ||
| + | |||
| + | Answer: Yes (see diagram) <math>\blacksquare</math> | ||
==2025 I Problem 1== | ==2025 I Problem 1== | ||
Revision as of 13:10, 3 August 2025
The Sharygin Olympiads are a prestigious series of geometry competitions named after Igor Fedorovich Sharygin (13/02/1937 – 12/03/2004), a renowned Soviet and Russian mathematician, teacher, and popularizer of science. Sharygin specialized in elementary geometry, authored numerous textbooks, and created many elegant problems. He also led the mathematics section of the Russian Soros Olympiads.
In his memory, Russia annually hosts the Geometry Olympiad for high school students, known as the Sharygin Olympiad. It consists of two stages: a correspondence round held from January to March, and a final round. The competition is open to Russian students in grades 8 to 11 and is also accessible to international high-school students.
Usually final round hosted near Dubna in Moscow region and in some other country (India,...) During the final round, participants present their solutions orally to a jury, using drafts and diagrams to support their reasoning.
Selected problems from these Olympiads are published, labeled by the year and serial number. The published solutions may differ from the original ones proposed during the contest.
Contents
- 1 2025 II Problem 8 1
- 2 2025 II Problem 8 2
- 3 2025 II Problem 8 3
- 4 2025 II Problem 8 4
- 5 2025 II Problem 8 5
- 6 2025 II Problem 8 6
- 7 2025 II Problem 8 7
- 8 2025 II Problem 8 8
- 9 2025 II Problem 9 1
- 10 2025 II Problem 9 2
- 11 2025 II Problem 9 3
- 12 2025 II Problem 9 4
- 13 2025 II Problem 9 5
- 14 2025 II Problem 9 6
- 15 2025 II Problem 9 7
- 16 2025 II Problem 9 8
- 17 2025 II Problem 10 1
- 18 2025 II Problem 10 2
- 19 2025 II Problem 10 3
- 20 2025 I Problem 1
- 21 2025 I Problem 2
- 22 2025 I Problem 3
- 23 2025 I Problem 4
- 24 2025 I Problem 5
- 25 2025 I Problem 6
- 26 2025 I Problem 7
- 27 2025 I Problem 8
- 28 2025 I Problem 9
- 29 2025 I Problem 10
- 30 2025 I Problem 11
- 31 2025 I Problem 12
- 32 2025 I Problem 13
- 33 2025 I Problem 14
- 34 2025 I Problem 15
- 35 2025 I Problem 16
- 36 2025 I Problem 17
- 37 2025 I Problem 18
- 38 2025 I Problem 19
- 39 2025 I Problem 20
- 40 2025 I Problem 21
- 41 2025 I Problem 22
- 42 2025 I Problem 23
- 43 2025 I Problem 24
- 44 Proof
- 45 2024 II Problem 6
- 46 2024 II Problem 2(8)
- 47 2024 II Problem 4(8)
- 48 2024 II Problem 3(9)
- 49 2024 II Problem 4(9)
- 50 2024 II Problem 5(9)
- 51 2024 II Problem 7(9)
- 52 2024 II Problem 7(10)
- 53 2024 I Problem 2
- 54 2024 I Problem 8
- 55 2024 I Problem 9
- 56 2024 I Problem 12
- 57 2024 I Problem 14
- 58 2024 I Problem 15
- 59 2024 I Problem 16
- 60 2024 I Problem 17
- 61 2024 I Problem 18
- 62 2024 I Problem 19
- 63 2024 I Problem 20
- 64 2024 I Problem 21
- 65 2024 I Problem 22
- 66 One-to-one mapping of the circle
- 67 2024 I Problem 23
- 68 The problem from MGTU
- 69 The trapezoid problem from MGTU
2025 II Problem 8 1
An inscribed pentagon ![]() with equal diagonals
with equal diagonals ![]() be given.
be given. ![]() and
and ![]() intersect diagonal
intersect diagonal ![]() at points
at points ![]() and
and ![]() respectively. It is known that
respectively. It is known that ![]()
Prove that the point symmetrical to ![]() with respect to the midpoint of
with respect to the midpoint of ![]() lies on line
lies on line ![]() (I.Kukharchuk, E.Galakhova.)
(I.Kukharchuk, E.Galakhova.)
Proof
![]()
![]()
![]() Let
Let ![]() be the midpoint
be the midpoint ![]() be the point symmetrical to
be the point symmetrical to ![]() with respect
with respect ![]() is the parallelogram.
is the parallelogram.
Therefore ![]() and
and ![]() are parallelograms
are parallelograms ![]()
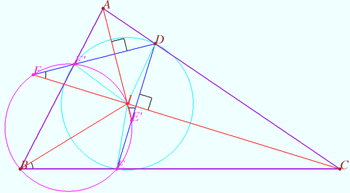
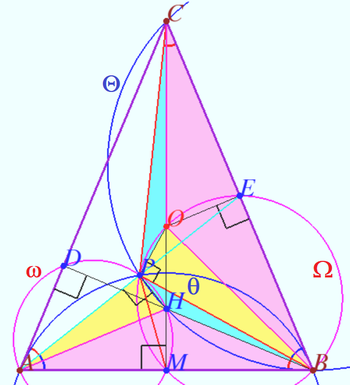
2025 II Problem 8 2
Let triangle ![]() with height
with height ![]() be given.
be given. ![]() and
and ![]() are the bisectors of
are the bisectors of ![]() and
and ![]() respectively.
respectively.
Prove that the curcumcenter ![]() of
of ![]() coincides with the incenter
coincides with the incenter ![]() of
of ![]() if and only if
if and only if ![]() (L.Emelyanov)
(L.Emelyanov)
Proof
Note that the points ![]() and
and ![]() lie on the bisector of
lie on the bisector of ![]() since the altitude of
since the altitude of ![]() is isogonally conjugate to radius
is isogonally conjugate to radius ![]()
1. Let ![]() Then
Then ![]() is the bisector of the
is the bisector of the ![]() so point
so point ![]() lies on the bisector
lies on the bisector ![]() is cyclic, so
is cyclic, so ![]() .
.
![]()
![]()
2. Let ![]() Then
Then ![]()
![]() so
so ![]() is cyclic
is cyclic ![]() is the bisector of
is the bisector of ![]() is the incenter of
is the incenter of ![]()
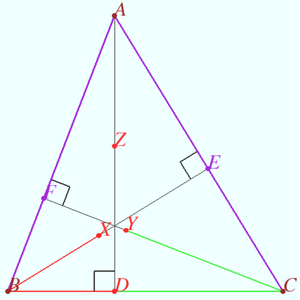
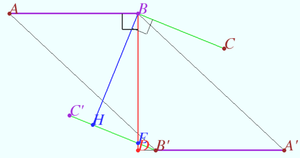
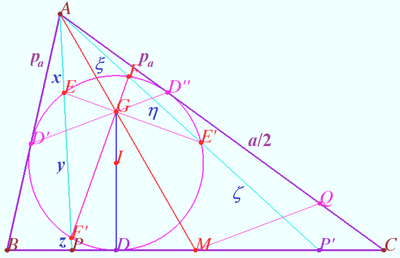
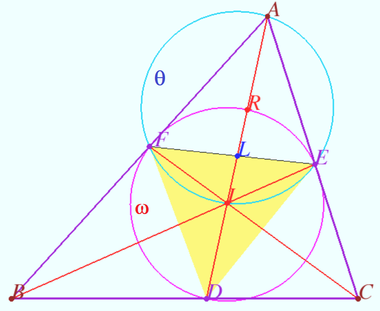
2025 II Problem 8 3
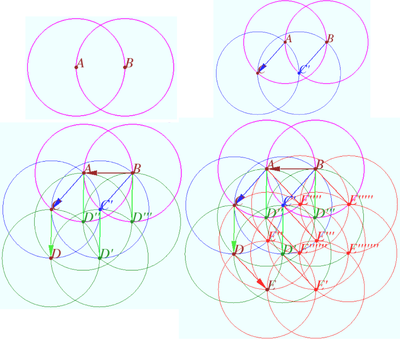
Is it possible to mark more than six points on a plane that do not lie on the same line and paint them in three colors so that on any line passing through two points of different colors there is exactly one more marked point, painted in a third color? (F. Nilov)
Answer: Yes (see diagram) ![]()
2025 II Problem 8 4
Let triangle ![]() with bisectors
with bisectors ![]() and
and ![]() be given. Let
be given. Let ![]() be the midpoint of arc
be the midpoint of arc ![]() of the circumcircle of
of the circumcircle of ![]() that does not contain point
that does not contain point ![]() The circumcircles of triangles
The circumcircles of triangles ![]() and
and ![]() intersect lines
intersect lines ![]() and
and ![]() at points
at points ![]() and
and ![]() respectively.
respectively.
Prove that the incenter ![]() of
of ![]() lies on
lies on ![]() (L. Shatunov)
(L. Shatunov)
Proof
Let ![]() be the point with the property
be the point with the property ![]()
![]()
![]() Denote
Denote ![]()
![]()
![]() is cyclic,
is cyclic, ![]()
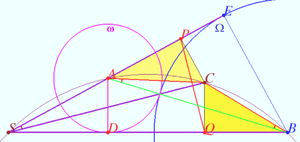
2025 II Problem 8 5
Let a right triangle ![]() be given. The distance from
be given. The distance from ![]() to the bisector of the acute angle is equal to a quarter of the hypotenuse.
to the bisector of the acute angle is equal to a quarter of the hypotenuse.
Find the possible values of the smallest angle of the triangle? (M. Volchkevich)
Answer: ![]()
2025 II Problem 8 6
Let a convex quadrilateral ![]() with angles
with angles ![]() Circles with diameters
Circles with diameters ![]() and
and ![]() intersect at points
intersect at points ![]() and
and ![]()
Prove that ![]() (I. Mikhailov)
(I. Mikhailov)
See diagram.![]()
2025 II Problem 8 7
A regular triangle ![]() is inscribed in a circle
is inscribed in a circle ![]() Circles
Circles ![]() with centers
with centers ![]() respectively pass through a point
respectively pass through a point ![]() lying on
lying on ![]() and are tangent to one line.
and are tangent to one line.
Prove that there exists a line tangent to two of these circles and passing through the vertex of ![]() (K. Belsky)
(K. Belsky)
Proof
Notation is shown in the diagram. WLOG,![]()
![]() is the common tangent,
is the common tangent, ![]() is the midpoint of
is the midpoint of ![]() is symmetrical to
is symmetrical to ![]() with respect
with respect ![]()
Well known that ![]()
The line symmetrical ![]() with respect
with respect ![]() is tangent to
is tangent to ![]() and
and ![]() and contain the point
and contain the point ![]()
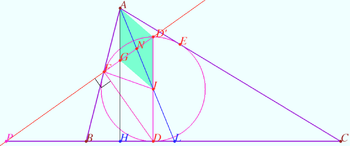
2025 II Problem 8 8
Let a convex pentagon ![]() be cut out of paper. Let
be cut out of paper. Let
![]()
![]() Construct the perpendicular from
Construct the perpendicular from ![]() to the line
to the line ![]() using only a ruler and drawing no more than six lines. Lines can only be drawn inside the pentagon. You can't bend the paper. (A. Blinkov)
using only a ruler and drawing no more than six lines. Lines can only be drawn inside the pentagon. You can't bend the paper. (A. Blinkov)
Solution
Notation is shown in the diagram, ![]()
![]()
![]()
![]() is the
is the ![]() excenter of
excenter of ![]()
Therefore ![]() is symmetrical to
is symmetrical to ![]() with respect to
with respect to ![]() is symmetrical to
is symmetrical to ![]() with respect to
with respect to ![]()
![]()
![]()
![]() are altitudes of
are altitudes of ![]() which are crossed at orthocenter
which are crossed at orthocenter ![]()
Construction
Segments ![]() and
and ![]() crossed at points
crossed at points ![]() and
and ![]()
Segments ![]() and
and ![]() crossed at point
crossed at point ![]()
Line ![]() is the perpendicular to
is the perpendicular to ![]()
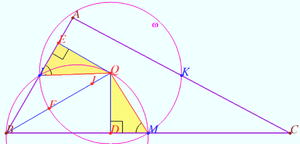
2025 II Problem 9 1
Heights ![]() of acute angled
of acute angled ![]() intersect at point
intersect at point ![]() Points
Points ![]() are symmetric to
are symmetric to ![]() with respect to
with respect to ![]() respectively.
respectively.
Prove that the nine points circles of triangles ![]() and
and ![]() are tangent. (Ya. Shcherbatov)
are tangent. (Ya. Shcherbatov)
Proof
Denote ![]() the midpoints of
the midpoints of ![]()
It is known that the circles are tangent iff ![]()
![]()
![]()
![]()
![]()
![]()
2025 II Problem 9 2
Several points were marked on a plane and painted in four colors so that on any circle passing through points of three different colors there lies exactly one more marked point, painted in the fourth color.
Do all the marked points necessarily lie on single circle? (F. Nilov)
Answer: No.![]()
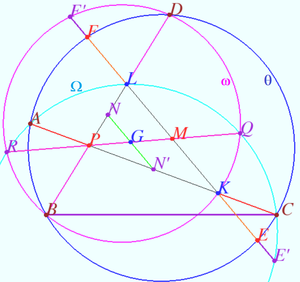
2025 II Problem 9 3
Let triangle ![]() and lines
and lines ![]() and
and ![]() be given. Line
be given. Line ![]() intersects lines
intersects lines ![]() at points
at points ![]() respectively, and line
respectively, and line ![]() intersects lines
intersects lines ![]() at points
at points ![]() where
where ![]() and
and ![]() are symmetrical with respect to the midpoint of
are symmetrical with respect to the midpoint of ![]() and
and ![]() are symmetrical with respect to the midpoint of
are symmetrical with respect to the midpoint of ![]() and
and ![]() are symmetrical with respect to the midpoint of
are symmetrical with respect to the midpoint of ![]()
Prove that ![]() if and only if
if and only if ![]() and
and ![]() are Simson lines for
are Simson lines for ![]() (for some points of circle
(for some points of circle ![]() (L.Emelyanov)
(L.Emelyanov)
Proof
1. Let ![]() be the centroid of
be the centroid of ![]() be the midpoints of
be the midpoints of ![]() is the common centroid of triangles
is the common centroid of triangles ![]()
Let us perform the homothety centered at ![]() with coefficient
with coefficient ![]()
Point ![]() maps into point
maps into point ![]()
![]() So
So ![]() is the midpoint of
is the midpoint of ![]()
Similarly, ![]() maps into
maps into ![]() maps into
maps into ![]() line
line ![]() maps into
maps into ![]()
WLOG, in the case shown on the diagram line ![]() is Newton-Gauss line of quadrilateral
is Newton-Gauss line of quadrilateral ![]()
It is known that this line is perpendicular to Simson line of the Miquel Point ![]() of complete quadrilateral
of complete quadrilateral ![]()
Similarly, such result one can get for line ![]()
2. If ![]() is the diameter of
is the diameter of ![]() then Simson lines of points
then Simson lines of points ![]() and
and ![]() are perpendicular.
are perpendicular. ![]()
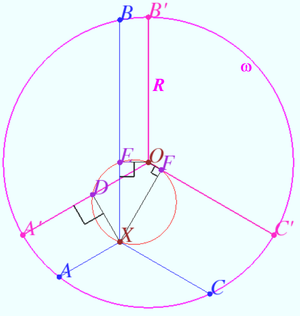
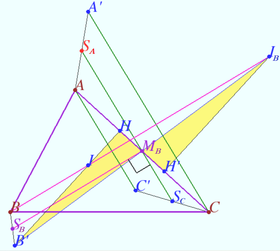
2025 II Problem 9 4
Let an inscribed quadrilateral ![]() and the orthocenter
and the orthocenter ![]() of
of ![]() be given.
Line
be given.
Line ![]() is parallel to
is parallel to ![]() Line
Line ![]() is parallel to
is parallel to ![]()
Prove that line ![]() divides segment
divides segment ![]() in half. (E. Volokitin)
in half. (E. Volokitin)
Proof
Denote ![]()
![]()
![]() It is known that under this condition:
It is known that under this condition:
- the projections of the point ![]() onto the lines
onto the lines ![]() lie on the circle
lie on the circle ![]()
- there is a point that is isogonally conjugate to point ![]() with respect to
with respect to ![]()
Point ![]() is isogonally conjugate to point
is isogonally conjugate to point ![]() with respect to
with respect to ![]() and
and ![]() is isogonally conjugate to point
is isogonally conjugate to point ![]() with respect to
with respect to ![]()
The foots of perpendiculars from ![]() onto the lines
onto the lines ![]() and
and ![]() points
points ![]() and
and ![]() and foot of perpendiculars from
and foot of perpendiculars from ![]() onto
onto ![]() point
point ![]() lie on Nine-point circle of
lie on Nine-point circle of ![]() so it is
so it is ![]()
Let the foots of perpendiculars from ![]() and
and ![]() onto
onto ![]() be
be ![]() and
and ![]() respectively,
respectively, ![]()
Midpoint ![]() the point
the point ![]() Let
Let ![]() be the circle
be the circle ![]()
We use the Reim's theorem for circles ![]() and
and ![]() and get
and get ![]()
Let us perform the homothety centered at ![]() with coefficient
with coefficient ![]() It maps
It maps ![]() to
to ![]() point
point ![]() to
to ![]() point
point ![]() to point
to point ![]() segment
segment ![]() to segment
to segment ![]()
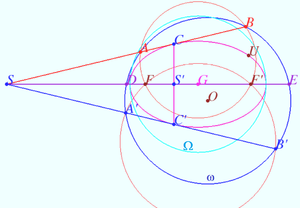
2025 II Problem 9 5
Let triangle ![]() with heights
with heights ![]() and
and ![]() be given. The internal bisectors of angles
be given. The internal bisectors of angles ![]() and
and ![]() intersect at point
intersect at point ![]() and the external ones at point
and the external ones at point ![]() Prove that
Prove that ![]() (I. Mikhailov)
(I. Mikhailov)
Proof
![]() is the chord of the circle with diameter
is the chord of the circle with diameter ![]()
![]() is the chord of the circle with diameter
is the chord of the circle with diameter ![]()
![]() only if
only if ![]() which is impossible.
which is impossible. ![]()
2025 II Problem 9 6
Let triangle ![]() with circumcircle
with circumcircle ![]() be given. Tangents to
be given. Tangents to ![]() drawn at points
drawn at points ![]() and
and ![]() intersect at point
intersect at point ![]() Segments
Segments ![]() and
and ![]() intersect at point
intersect at point ![]() Bisectors (as rays) of angles
Bisectors (as rays) of angles ![]() and
and ![]() intersect
intersect ![]() at points
at points ![]() and
and ![]()
Prove that points ![]() and
and ![]() are colinear. (D.Brodsky)
are colinear. (D.Brodsky)
Proof
Let us make a projective transformation that preserves the circle ![]() and maps
and maps ![]() to its center.
to its center.
The line ![]() maps into diameter of
maps into diameter of ![]() so images
so images ![]() and
and ![]() are parallel, points
are parallel, points ![]() maps into points of infinity.
maps into points of infinity.
![]() maps in line parallel to tangents in points
maps in line parallel to tangents in points ![]() and
and ![]() so images
so images ![]() and
and ![]() are perpendicular.
are perpendicular.
The cross-ratio of four coplanar and concurrent lines ![]() and
and ![]() is
is
![]() The cross-ratio is the invariant under projective transformation.
The cross-ratio is the invariant under projective transformation.
In the image plane ![]() so we get
so we get
![]() Preimage
Preimage ![]() contain point
contain point ![]()
2025 II Problem 9 7
Let triangle ![]() and point
and point ![]() at the bisector of the segment
at the bisector of the segment ![]() be given. Lines
be given. Lines ![]() and
and ![]() intersect at point
intersect at point ![]() and lines
and lines ![]() and
and ![]() intersect at point
intersect at point ![]() Let
Let ![]() be the midpoint of
be the midpoint of ![]() be the second intersection point of circles
be the second intersection point of circles ![]() and
and ![]()
Prove that the center ![]() of circle
of circle ![]() lies on the fixed line. ( N.Shteinberg)
lies on the fixed line. ( N.Shteinberg)
Proof
The main idea is that on the circle ![]() in addition to
in addition to ![]() there is a fixed point
there is a fixed point ![]() (independent from
(independent from ![]() and the fixed line is the bisector of
and the fixed line is the bisector of ![]()
Point ![]() is determined only by the triangle
is determined only by the triangle ![]() We need to find point at
We need to find point at ![]() that does not depend on
that does not depend on ![]() This point turns out to be the point
This point turns out to be the point ![]() at the median
at the median ![]() which satisfies the condition
which satisfies the condition ![]() We use the baricentric coordinates.
We use the baricentric coordinates.
Point ![]() where
where ![]()
Point ![]()
Then ![]()
Point ![]() is the Miquel point of complete quadrilateral
is the Miquel point of complete quadrilateral ![]()
Any circle has the equation ![]()
Circle ![]() has coefficients
has coefficients ![]()
Circle ![]() has coefficients
has coefficients ![]()
Point 
Point ![]() Circle
Circle ![]() has coefficients
has coefficients
![]() where
where ![]()
Substituting the expression for ![]() into the circle
into the circle ![]() formula we see that this point lies on this circle.
formula we see that this point lies on this circle. ![]()
vladimir.shelomovskii@gmail.com, vvsss
2025 II Problem 9 8
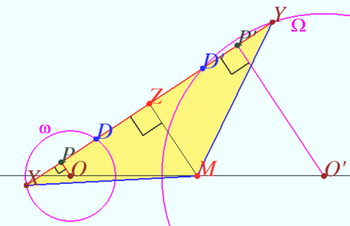
Restore the bicentric quadrilateral ![]() by the incenter
by the incenter ![]() the point
the point ![]() of intersection of the tangents to the circumcircle at points
of intersection of the tangents to the circumcircle at points ![]() and the point
and the point ![]() of intersection of the tangents to the circumcircle at points
of intersection of the tangents to the circumcircle at points ![]() (S. Arutyunyan)
(S. Arutyunyan)
Construction
1. We construct orthocenter ![]() of
of ![]() and heights
and heights ![]() and
and ![]()
2. We construct circle ![]() centered at
centered at ![]() with radius
with radius ![]() Let
Let ![]() be the tangent line to
be the tangent line to ![]()
3. Let ![]() cross
cross ![]() at points
at points ![]() and
and ![]() and
and ![]() at point
at point ![]()
4. Let ![]() be the line throught point
be the line throught point ![]() parallel to
parallel to ![]() This line cross circle
This line cross circle ![]() centered at
centered at ![]() with radius
with radius ![]() at points
at points ![]() and
and ![]()
The required quadrilateral ![]() has been constructed.
has been constructed.
To justify the construction, it is necessary to prove that if ![]() is bicentric quadrilateral,
is bicentric quadrilateral, ![]() is the pole of
is the pole of ![]() then:
then:
1. ![]()
2. ![]()
3. The circumcenter ![]() of
of ![]() is the orthocenter of
is the orthocenter of ![]()
4. ![]()
Proof
1. ![]()
![]()
2. ![]() where
where ![]()
![]()
![]() 3.
3. ![]() is the polar of
is the polar of ![]() with respect
with respect ![]() is the polar of
is the polar of ![]() with respect
with respect ![]()
![]() is the pole of
is the pole of ![]()
It is known that points ![]() and
and ![]() are collinear, so
are collinear, so ![]()
![]()
4. ![]() lies at radical axes
lies at radical axes ![]() and
and ![]()
![]() polar
polar ![]() with respect
with respect ![]() polar
polar ![]() with respect
with respect ![]()
![]() is the pole of
is the pole of ![]() with respect
with respect ![]()
2025 II Problem 10 1
Let a convex quadrilateral ![]() be given. Let
be given. Let ![]() be the midpoint
be the midpoint ![]() Two parallelograms
Two parallelograms ![]() and
and ![]() are inscribed in
are inscribed in ![]() such that
such that ![]() and
and ![]() lie on the sides
lie on the sides ![]() respectively.
respectively.
Is it possible that the area of one parallelogram is less than half the area of the quadrilateral, and the area of the other is greater? (I. Bogdanov)
Answer: No.
Proof
Case 1. ![]()
![]() is the midline of trapezium
is the midline of trapezium ![]()
![]()
Case 2. ![]()
![]() Let points
Let points ![]() be such point that
be such point that ![]() and
and ![]() are collinear and
are collinear and ![]()
It is known that ![]()
It is known that there is Varignon parallelogram ![]() where
where ![]() Midpoints of
Midpoints of ![]() and
and ![]() the point
the point ![]() is the single point,
is the single point, ![]() and
and ![]() are not parallel, therefore
are not parallel, therefore ![]()
![]()
Case 3. ![]() Similarly we get
Similarly we get ![]()
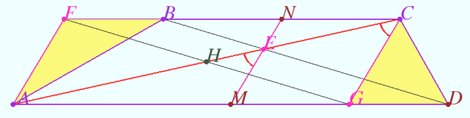
2025 II Problem 10 2
Let a non-isosceles triangle ![]() and it’s incenter
and it’s incenter ![]() be given. Points
be given. Points ![]() are isogonally conjugate points such that
are isogonally conjugate points such that ![]()
Prove that ![]() (E.Volokitin)
(E.Volokitin)
Proof
We use baricentric coordinates.
Line ![]() is
is ![]()
Line ![]() is
is ![]()
![]()
vladimir.shelomovskii@gmail.com, vvsss
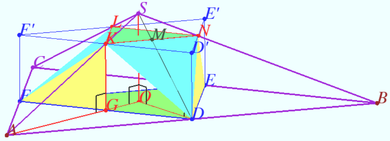
2025 II Problem 10 3
Is it possible to take six points ![]() in general position in space so that triangles
in general position in space so that triangles ![]() and
and ![]() are “linked”, but two triangles corresponding to any other partition of these points into two triplets are not? Two triangles in space are “linked” if the contour of one intersects the interior of the other at a single point. (E. Alkin, A. Skopenkov)
are “linked”, but two triangles corresponding to any other partition of these points into two triplets are not? Two triangles in space are “linked” if the contour of one intersects the interior of the other at a single point. (E. Alkin, A. Skopenkov)
Answer: Yes (see diagram) ![]()
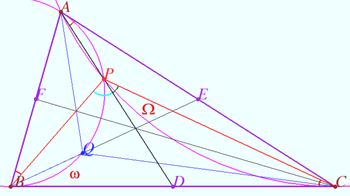
2025 I Problem 1
Let ![]() be the incenter of a triangle
be the incenter of a triangle ![]() be an arbitrary point of sideline
be an arbitrary point of sideline ![]() and
and ![]() be the common points of the perpendicular from
be the common points of the perpendicular from ![]() to the bisector
to the bisector ![]() with
with ![]() and
and ![]() respectively. Define similarly the points
respectively. Define similarly the points ![]()
Prove that ![]() and
and ![]() are concyclic.(Shvetzov)
are concyclic.(Shvetzov)
Proof
![]()
![]()
![]() is concyclic.
is concyclic.
Similarly ![]() is concyclic.
is concyclic.
![]() is common in triangles
is common in triangles ![]() and
and ![]()
![]() is concyclic
is concyclic ![]() is concyclic.
is concyclic.
2025 I Problem 2
Four points on the plane are not concyclic, and any three of them are not collinear. Prove that there exists a point ![]() such that the reflection of each of these four points about
such that the reflection of each of these four points about ![]() lies on the circle passing through three remaining points. (Kuznetsov)
lies on the circle passing through three remaining points. (Kuznetsov)
Proof
Let a point symmetrical to ![]() with respect to
with respect to ![]() lie on the circle
lie on the circle ![]() We perform a homothety with center
We perform a homothety with center ![]() and coefficient
and coefficient ![]() The image
The image ![]() circle
circle ![]() contains the midpoints of the segments
contains the midpoints of the segments ![]() and the point
and the point ![]()
Therefore, the statement of the problem is equivalent to the fact that the four circles passing through the midpoints of the segments connecting each point with the three remaining ones had a common point.
Denote ![]() the midpoint of segment
the midpoint of segment ![]() similarly define
similarly define ![]()
![]()
Let ![]()
We use the properties of the midlines and get ![]()
WLOG, analize the case, shown in diagram.
![]() In
In ![]() we get
we get ![]()
In ![]() we get
we get ![]()
So
![]()
![]()
![]() Similarly,
Similarly, ![]()
2025 I Problem 3
An excircle centered at ![]() touches the side
touches the side ![]() of a
of a ![]() at point
at point ![]() Prove that the pedal circles of
Prove that the pedal circles of ![]() with respect to the triangles
with respect to the triangles ![]() and
and ![]() are congruent. (Belsky)
are congruent. (Belsky)
Proof
Let the foots of perpendiculars from the point ![]() to
to ![]() and
and ![]() be
be ![]() and
and ![]() respectively, point
respectively, point ![]() be the midpoint
be the midpoint ![]() be the semiperimeter of
be the semiperimeter of ![]()
![]() excircle touch the sides
excircle touch the sides ![]() and
and ![]() at points
at points ![]() and
and ![]() respectively.
respectively.
The points ![]() and
and ![]() are concyclic
are concyclic ![]() is the center of this circle), so
is the center of this circle), so ![]()
![]() is the midline of
is the midline of ![]()
Similarly, ![]()
The rotation centered at ![]() with angle
with angle ![]() maps
maps ![]() into
into ![]() therefore this triangles (and circumcircles) are congruent.
therefore this triangles (and circumcircles) are congruent. ![]()
Proof 2
Denote ![]()
![]()
WLOG,![]()
Angles with vertex ![]() are
are ![]()
![]()
![]()
The points ![]() and
and ![]() are concyclic
are concyclic
![]() is the diameter of this circle), so
is the diameter of this circle), so ![]()
The points ![]() and
and ![]() are concyclic
are concyclic
![]() is the diameter of this circle), so
is the diameter of this circle), so ![]()
![]()
Similarly, ![]()
The points ![]() and
and ![]() are concyclic
are concyclic
![]() is the diameter of this circle), so
is the diameter of this circle), so ![]()
![]()
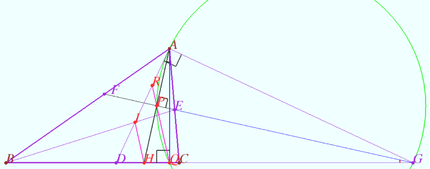
2025 I Problem 4
Let a triangle ![]() with the bisector
with the bisector ![]() of
of ![]() and point
and point ![]() be given. Let the line
be given. Let the line ![]() be the bisector of
be the bisector of ![]() Prove that points
Prove that points ![]() and
and ![]() are concyclic. (Shcherbatov)
are concyclic. (Shcherbatov)
Proof
Denote ![]() is rhomb
is rhomb ![]()
![]()
![]() are concyclic.
are concyclic.![]()
Proof 2
Denote ![]()
We use the properties of bisectors and get:
![]() so
so ![]() is the harmonic conjugate of
is the harmonic conjugate of ![]() with respect to
with respect to ![]() and
and ![]() and the cross-ratio
and the cross-ratio ![]()
Under projecting a straight line ![]() to
to ![]() from point
from point ![]() the cross-ratio is preserved,
the cross-ratio is preserved, ![]() maps into
maps into ![]() maps into
maps into ![]() maps into
maps into ![]() maps into point in infinity, so
maps into point in infinity, so  is the midpoint
is the midpoint ![]()
![]() is parallelogram, so
is parallelogram, so ![]()
![]()
![]() is the isosceles trapezoid, which is the cyclic quadrilateral.
is the isosceles trapezoid, which is the cyclic quadrilateral.![]()
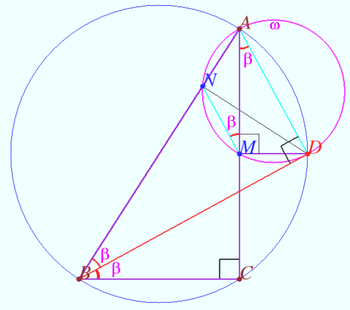
2025 I Problem 5
Let ![]() be the midpoint of the cathetus
be the midpoint of the cathetus ![]() of a right-angled
of a right-angled ![]() The perpendicular from
The perpendicular from ![]() to the bisector of
to the bisector of ![]() meets
meets ![]() at point
at point ![]()
Prove that the circumcircle of triangle ![]() touches the bisector of angle
touches the bisector of angle ![]() (Shvetsov)
(Shvetsov)
Proof
Let the bisector of ![]() meets circumcircle of
meets circumcircle of ![]() at point
at point ![]()
![]() so circle
so circle ![]() with diameter
with diameter ![]() touches the bisector
touches the bisector ![]()
![]() is the midpoint of arc
is the midpoint of arc ![]() so
so ![]()
![]()
![]()
![]()
2025 I Problem 6
One bisector of a given triangle is parallel to one sideline of its Nagel triangle.
Prove that one of two remaining bisectors is parallel to another sideline of the Nagel triangle. (Emelyanov)
Proof
Let ![]() be the given triangle,
be the given triangle, ![]() be the Nagel triangle
be the Nagel triangle ![]() be the bisectors,
be the bisectors, ![]()
It is known that ![]()
WLOG, ![]()
![]()
![]()
![]()
Proof 2
Denote ![]() semiangles of
semiangles of ![]() the
the ![]() excenters,
excenters, ![]() is
is ![]() excircle,
excircle, ![]() is it’s radius,
is it’s radius, ![]()
![]()
![]() points
points ![]() are collinear.
are collinear.
![]() We use the Sine Law for
We use the Sine Law for ![]() and get:
and get:
![]()
![]()
![]() is the solution.
If
is the solution.
If ![]() then
then ![]()
![]()
It is impossible, so ![]()
![]() is parallelogram, so
is parallelogram, so ![]()
2025 I Problem 7
Let ![]() be the incenter and the
be the incenter and the ![]() excenter of a triangle
excenter of a triangle ![]() be the touching points of the incircle with
be the touching points of the incircle with ![]() respectively;
respectively; ![]() be the common point of
be the common point of ![]() and
and ![]() The perpendicular to
The perpendicular to ![]() from
from ![]() meets
meets ![]() at point
at point ![]()
Prove that points ![]() and
and ![]() are concyclic. (Shcherbatov)
are concyclic. (Shcherbatov)
Proof
Denote ![]() and
and ![]() are sides of
are sides of ![]() and it’s semiperimeter.
and it’s semiperimeter. ![]() is the touching points of the incircle with
is the touching points of the incircle with ![]()
![]() is the touching points of A-excircle with
is the touching points of A-excircle with ![]()
![]()
It is known that ![]() is the Gergonne point,
is the Gergonne point, ![]() One can use formulas for barycentric coordinates of
One can use formulas for barycentric coordinates of ![]() or formulas of crossing segments
or formulas of crossing segments ![]() and
and ![]() and get
and get ![]()
![]()
![]()
![]()
![]()
We use the Sine Law for triangles ![]() and
and ![]() and get:
and get:
![]()
Therefore ![]()
2025 I Problem 8
The diagonals of a cyclic quadrilateral ![]() meet at point
meet at point ![]() Points
Points ![]() and
and ![]() lie on
lie on ![]() and
and ![]() respectively in such a way that
respectively in such a way that ![]() and
and ![]()
Prove that the line joining the common points of circles ![]() and
and ![]() passes through the mass-center of
passes through the mass-center of ![]() (Konyshev)
(Konyshev)
Proof
Denote ![]()
![]() is the midpoint of
is the midpoint of ![]() and
and ![]() is the midpoint of
is the midpoint of ![]() and
and ![]() is the midpoint of
is the midpoint of ![]() is the midpoint of
is the midpoint of ![]()
It is clear that ![]() is the mass-center of
is the mass-center of ![]()
We use properties of the crossing chords and get:
![]()
![]() Similarly,
Similarly, ![]()
![]()
![]() is the median of
is the median of ![]() so point
so point ![]() lies on
lies on ![]() which is the part of the radical axis of
which is the part of the radical axis of ![]() and
and ![]()
![]()
Proof 2
![]() is the radical axis of
is the radical axis of ![]() and
and ![]() is the radical axis of
is the radical axis of ![]() and
and ![]() is the radical center of
is the radical center of ![]() and
and ![]() is the radical axis of
is the radical axis of ![]() and
and ![]()
It is known that the difference in the power of a point relative to a fixed pair of circles is a linear function of the coordinates of the point. Denote ![]()
Denote power of the point ![]() as
as ![]()
![]()
![]()
![]()
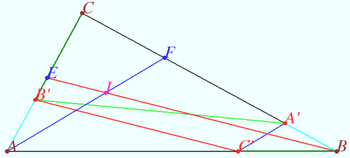
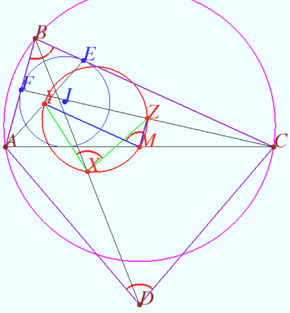
2025 I Problem 9
The line ![]() passing through the orthocenter
passing through the orthocenter ![]() of a
of a ![]() and parallel to
and parallel to ![]() meets
meets ![]() and
and ![]() at points
at points ![]() and
and ![]() respectively. The line passing through the circumcenter of the triangle
respectively. The line passing through the circumcenter of the triangle ![]() and parallel to the median
and parallel to the median ![]() meets
meets ![]() at point
at point ![]()
Prove that the length of segment ![]() is three times greater than the difference of
is three times greater than the difference of ![]() and
and ![]() (Mardanov)
(Mardanov)
Proof
Denote ![]()
![]()
![]() is the centroid, so
is the centroid, so ![]()
![]()
![]()
![]()
2025 I Problem 10
An acute-angled triangle with one side equal to the altitude from the opposite vertex is cut from paper. Construct a point inside this triangle such that the square of the distance from it to one of the vertices equals the sum of the squares of distances to the remaining two vertices. No instruments are available, it is allowed only to fold the paper and to mark the common points of folding lines.(Evdokimov)
The Huzita–Justin axioms are a set of rules related to the mathematical principles of origami, describing the operations that can be made when folding a piece of paper.
The axioms are as follows:
1. Given two distinct points ![]() and
and ![]() there is a unique fold that passes through both of them.
there is a unique fold that passes through both of them.
2. Given two distinct points ![]() and
and ![]() there is a unique fold that places
there is a unique fold that places ![]() onto
onto ![]()
3. Given two lines ![]() and
and ![]() there is a fold that places
there is a fold that places ![]() onto
onto ![]()
4. Given a point ![]() and a line
and a line ![]() there is a unique fold perpendicular to
there is a unique fold perpendicular to ![]() that passes through point
that passes through point ![]()
5. Given two points ![]() and
and ![]() and a line
and a line ![]() there is a fold that places
there is a fold that places ![]() onto
onto ![]() and passes through
and passes through ![]()
6. Given two points ![]() and
and ![]() and two lines
and two lines ![]() and
and ![]() there is a fold that places
there is a fold that places ![]() onto
onto ![]() and
and ![]() onto
onto ![]()
7. Given point ![]() and two lines
and two lines ![]() and
and ![]() there is a fold that places
there is a fold that places ![]() onto
onto ![]() and is perpendicular to
and is perpendicular to ![]()
Solution
Let ![]() be the heights of
be the heights of ![]()
Let ![]() be the point such
be the point such ![]()
![]() Similarly
Similarly ![]()
We construct heights ![]() according the Axiom 4.
according the Axiom 4.
We construct bisector of angle ![]() , fold places line
, fold places line ![]() onto line
onto line ![]() (Axiom 3)
(Axiom 3)
We construct point ![]() symmetric to
symmetric to ![]() with respect bisector of
with respect bisector of ![]()
Solution 2
Let ![]() be the point such
be the point such ![]() WLOG
WLOG ![]()
![]() We construct height
We construct height ![]() according the Axiom 4.
according the Axiom 4.
We construct point ![]() using midpoint of
using midpoint of ![]()
We construct point ![]() a fold places
a fold places ![]() onto
onto ![]() and passes through
and passes through ![]() (Axiom 5)
(Axiom 5)
![]() We construct point
We construct point ![]() symmetric to
symmetric to ![]() with respect midpoint of
with respect midpoint of ![]()
2025 I Problem 11
A point ![]() is the origin of three rays such that the angle between any two of them equals
is the origin of three rays such that the angle between any two of them equals ![]() Let
Let ![]() be an arbitrary circle with radius
be an arbitrary circle with radius ![]() such that
such that ![]() lies inside it, and
lies inside it, and ![]() be the common points of the rays with this circle.
be the common points of the rays with this circle.
Find ![]() (Nilov)
(Nilov)
Answer: 3R.
Solution
The Fermat–Torricelli point of a triangle with largest angle at most 120° is a point such that:
- the sum of the three distances from each of the three vertices of the triangle to the point is the smallest possible,
- the angles subtended by the rays to the vertieces of the triangle at Fermat–Torricelli point are all equal to 120°.
Therefore, ![]() is the Fermat–Torricelli point,
is the Fermat–Torricelli point, ![]() where
where ![]() is the center of the circle. Equality is achieved when
is the center of the circle. Equality is achieved when ![]() coincides with
coincides with ![]()
Solution 2
Let ![]() be the circumcenter
be the circumcenter ![]() Define
Define ![]() and
and ![]() similarly.
similarly.
WLOG , ![]() lies in angle
lies in angle ![]() Let
Let ![]() be the foots of perpendiculars from
be the foots of perpendiculars from ![]() to
to ![]() and
and ![]() Let
Let ![]() be the foot of perpendiculars from
be the foot of perpendiculars from ![]() to
to ![]()
It is known that ![]()
![]()
![]()
![]() Solution 3
Solution 3
The triangle formed by the perpendiculars drawn at points ![]() to the rays
to the rays ![]() is regular.
is regular.
The sum ![]() is equal to the height of this regular triangle.
is equal to the height of this regular triangle.
The sides of this regular triangle have common points with ![]() , therefore its height (and side) is maximum if
, therefore its height (and side) is maximum if ![]() is an inscribed circle.
is an inscribed circle.
This means the sum is maximum if ![]() is the center of the circle.
is the center of the circle.![]()
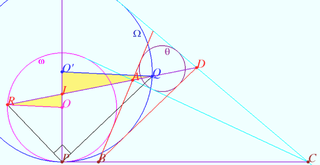
2025 I Problem 12
Let circles ![]() and
and ![]() centered at
centered at ![]() and
and ![]() be given,
be given, ![]() is the midpoint of
is the midpoint of ![]() Let
Let ![]() and
and ![]() be arbitrary points on
be arbitrary points on ![]() and
and ![]() respectively such that
respectively such that ![]()
Find the locus of the midpoints of segments ![]() (Shatunov)
(Shatunov)
Solution
Case 1
Let ![]() Then
Then ![]() so
so ![]() and
and ![]() coincide. Any point inside this circle belong the locus.
coincide. Any point inside this circle belong the locus.
Case 2
Circles ![]() and
and ![]() have not common point.
Denote
have not common point.
Denote ![]() midpoint of
midpoint of ![]() the midpoints of
the midpoints of ![]() and
and ![]()
![]()
![]()
![]() Therefore
Therefore ![]() lies on the radical axes of
lies on the radical axes of ![]() and
and ![]()
Let common external tangents crossed the radical axes at points ![]() and
and ![]() common internal tangents crossed the radical axes at points
common internal tangents crossed the radical axes at points ![]() and
and ![]()
For given point ![]() there are two points
there are two points ![]() and
and ![]()
![]() corresponding to the condition. Respectively, there are two points
corresponding to the condition. Respectively, there are two points ![]() and
and ![]() It seems obvious that for any point of these segments one can find points
It seems obvious that for any point of these segments one can find points ![]() and
and ![]() satisfying the condition. There was no need to prove this.
satisfying the condition. There was no need to prove this.
Case 3
Circles ![]() and
and ![]() are crossing. Common external tangents crossed the radical axes at points
are crossing. Common external tangents crossed the radical axes at points ![]() and
and ![]() and segment
and segment ![]() is the locus.
is the locus.![]()
2025 I Problem 13
Each two opposite sides of a convex ![]() gon are parallel. (Two sides are opposite if one passes
gon are parallel. (Two sides are opposite if one passes ![]() other sides moving from one side to another along the borderline of the
other sides moving from one side to another along the borderline of the ![]() gon.) The pair of opposite sides is called regular if there exists a common perpendicular to them such that its endpoints lie on the sides and not on their extensions.
gon.) The pair of opposite sides is called regular if there exists a common perpendicular to them such that its endpoints lie on the sides and not on their extensions.
Which is the minimal possible number of regular pairs? (Frankin)
Answer: 1
Proof
1. We need to prove that zero regular pair is impossible.
Suppose, all pairs are irregular. Let ![]() and
and ![]() be a pair of sides with the minimum distance
be a pair of sides with the minimum distance ![]() between them,
between them, ![]() and
and ![]() is the next irregular pare.
is the next irregular pare.
![]() gon is convex, so acute
gon is convex, so acute ![]() and
and ![]() cross
cross ![]() at point
at point ![]()
Let ![]() which contradicts the choice of the pair
which contradicts the choice of the pair ![]()
2. We need to show that exist ![]() gon with only
gon with only ![]() regular pair. WLOG, we do this for
regular pair. WLOG, we do this for ![]()
We use an obtuse angle ![]() and divide
and divide ![]() and
and ![]() into
into ![]() equal segments as shown in diagram.
equal segments as shown in diagram.
![]()
![]()
We construct the perpendicular to ![]() through
through ![]() and construct the center
and construct the center ![]() of
of ![]() gon such that
gon such that ![]() and
and ![]() lyes in the semiplane opposite to
lyes in the semiplane opposite to ![]()
Points ![]() and
and ![]() are symmetrical to points
are symmetrical to points ![]() and
and ![]() with respect
with respect ![]()
Only sides ![]() and
and ![]() are the regular pair.
are the regular pair.
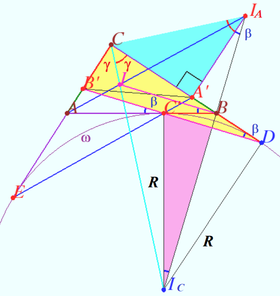
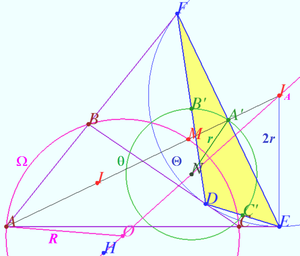
2025 I Problem 14
A point ![]() lies inside a triangle
lies inside a triangle ![]() on the bisector of angle
on the bisector of angle ![]() Let
Let ![]() and
and ![]() be the circles touching
be the circles touching ![]() and
and ![]() at
at ![]() and passing through
and passing through ![]() and
and ![]() be the common points of
be the common points of ![]() and
and ![]() with the circumcircle
with the circumcircle ![]() of
of ![]() (distinct from
(distinct from ![]() ) Prove that the circumcircles of the triangles
) Prove that the circumcircles of the triangles ![]() and
and ![]() are tangent. (L.Shatunov)
are tangent. (L.Shatunov)
Proof
Denote ![]()
![]()
![]() is the chord of
is the chord of ![]() is the chord of
is the chord of ![]()
It seems evident that iff ![]() then exist line through
then exist line through ![]() which is the common tangent to both of these circles.
which is the common tangent to both of these circles.
![]() is the tangent to
is the tangent to ![]()
![]()
So ![]() and quadrilateral
and quadrilateral ![]() is cyclic in
is cyclic in ![]()
Similarly, ![]() is cyclic.
is cyclic.
![]() are concyclic.
are concyclic.
![]()
Quadrilateral ![]() is cyclic in
is cyclic in ![]()
![]()
Proof 2
Let's perform the inversion centered at ![]() with radius
with radius ![]() In inversion plane images of
In inversion plane images of ![]() and
and ![]() need be parallel.
need be parallel.
As a result, points ![]() and
and ![]() maps into
maps into ![]() and
and ![]() maps into circle
maps into circle ![]() circle
circle ![]() maps into the line
maps into the line ![]() circle
circle ![]() maps into the line
maps into the line ![]()
By the properties of inversion, ![]()
![]()
![]() in the circle
in the circle ![]()
Therefore, the lines ![]() Their preimages
Their preimages ![]() and
and ![]() are tangent.
are tangent.![]()
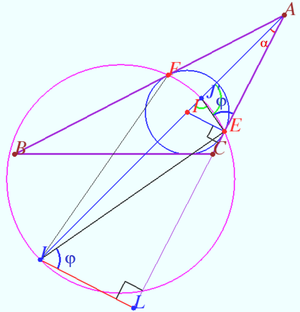
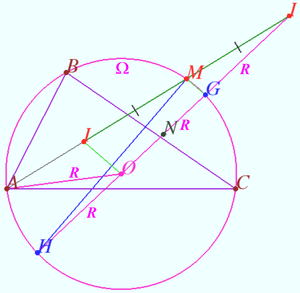
2025 I Problem 15
Let the point ![]() on the bisector of an acute angle with vertex
on the bisector of an acute angle with vertex ![]() be given. Let points
be given. Let points ![]() and
and ![]() be the foot from
be the foot from ![]() to the sidelines of the angle. The circle centered at
to the sidelines of the angle. The circle centered at ![]() with radius
with radius ![]() meets the sidelines at points
meets the sidelines at points ![]() and
and ![]() Denote
Denote ![]() the circle centered at
the circle centered at ![]() and tangent to ray
and tangent to ray ![]() the circle centered at
the circle centered at ![]() and tangent to ray
and tangent to ray ![]()
Prove that ![]() and
and ![]() are tangent. (Zaslavsky)
are tangent. (Zaslavsky)
Proof
Denote ![]()
![]()
![]()
![]()
![]()
![]() points
points ![]() are concyclic.
are concyclic.
![]()
2025 I Problem 16
The Feuerbach point of a scalene triangle lies on one of its bisectors. Prove that it bisects the segment between the corresponding vertex and the incenter. (Zaslavsky)
Proof
The Feuerbach hyperbola is a rectangular hyperbola passing through the vertices, orthocenter, incenter, Gergonne point, Nagel point and Schiffler point. The center of the hyperbola is the Feuerbach point.
If vertex ![]() incenter
incenter ![]() and Feuerbach point
and Feuerbach point ![]() are collinear,
are collinear, ![]() and
and ![]() need be on the different branches of hyperbola, therefore
need be on the different branches of hyperbola, therefore ![]() and
and ![]() are symmetrical with respect
are symmetrical with respect ![]()
Proof 2
Let given triangle be ![]() the incenter
the incenter ![]() the inradius
the inradius ![]() the Feuerbach point
the Feuerbach point ![]() is the point at
is the point at ![]() height such that
height such that ![]() be the midpoint of
be the midpoint of ![]()
It is known that points ![]() are collinear ( Feuerbach line).
are collinear ( Feuerbach line).
![]() is a scalene triangle, so
is a scalene triangle, so ![]() can not lie at
can not lie at ![]() and A-Feuerbach line not coincide with bisector
and A-Feuerbach line not coincide with bisector ![]()
The Feuerbach point lies on A-bisector therefore it coincide with ![]()
Proof 3
If the Feuerbach point of a scalene triangle lies on one of its bisectors, then the angle corresponding to this bisector is ![]() Feuerbach point of a scalene triangle
Denote
Feuerbach point of a scalene triangle
Denote ![]() the inradius and
the inradius and ![]() - this bisector. Then
- this bisector. Then
![]() Proof 4
Proof 4
Let ![]() be the midpoints
be the midpoints ![]() respectively. So the center
respectively. So the center ![]() of nine-point circle
of nine-point circle ![]() lies on
lies on ![]()
Let ![]() and
and ![]() be the foots from
be the foots from ![]() to
to ![]() and
and ![]()
![]() where
where ![]() is the circumradius of
is the circumradius of ![]()
![]() is a scalene triangle, so
is a scalene triangle, so ![]()
![]()
So quadrilateral ![]() is cyclic.
is cyclic. ![]() has the radius
has the radius ![]() and the center
and the center ![]() of
of ![]() lies on
lies on ![]()
![]()
2025 I Problem 17
Let ![]() be the circumcenter and the incenter of an acute-angled scalene triangle
be the circumcenter and the incenter of an acute-angled scalene triangle ![]() be the touching points of its excircle with the side
be the touching points of its excircle with the side ![]() and the extensions of
and the extensions of ![]() respectively. Prove that if the orthocenter
respectively. Prove that if the orthocenter ![]() of
of ![]() lies on the circumcircle of
lies on the circumcircle of ![]() then it is symmetric to the midpoint of the arc
then it is symmetric to the midpoint of the arc ![]() with respect to
with respect to ![]() (Puchkov, Utkin)
(Puchkov, Utkin)
Proof
Let ![]() be the midpoints of
be the midpoints of ![]() respectively.
respectively.
Let ![]() be A-excenter of
be A-excenter of ![]() and the circumcenter of
and the circumcenter of ![]() it’s radius
it’s radius ![]()
Let ![]() be the center of
be the center of ![]() and nine-points center of
and nine-points center of ![]()
Points ![]() are collinear at Euler line of
are collinear at Euler line of ![]()
![]() and
and ![]() are tangents,
are tangents, ![]() is the midpoint
is the midpoint ![]() so
so ![]() is the inversion of point
is the inversion of point ![]() with respect
with respect ![]() Similarly,
Similarly, ![]() and
and ![]() so
so ![]() is the inversion
is the inversion ![]() with respect
with respect ![]() Therefore centers
Therefore centers ![]() and
and ![]() are collinear.
are collinear.
Homothety centered at ![]() with coefficient
with coefficient ![]() maps
maps ![]() into
into ![]()
If ![]() than
than ![]() We use Euler formula
We use Euler formula
![]() and get
and get
![]()
![]() The midpoint
The midpoint ![]() lies on
lies on ![]() is the diameter of
is the diameter of ![]()
The midpoint of the arc ![]() point
point ![]() is the midpoint of
is the midpoint of ![]() is the bisector of
is the bisector of ![]()
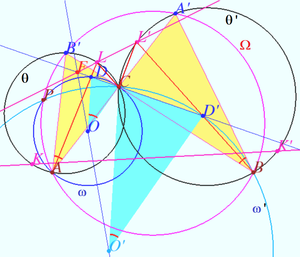
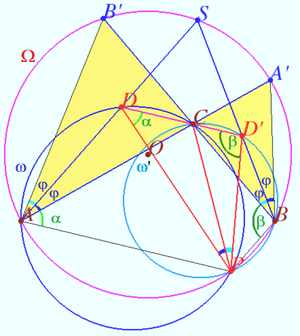
2025 I Problem 18
Let ![]() be a quadrilateral such that the excircles
be a quadrilateral such that the excircles ![]() and
and ![]() of triangles
of triangles ![]() and
and ![]() touching their sides
touching their sides ![]() and
and ![]() respectively touch the extension of
respectively touch the extension of ![]() at the same point
at the same point ![]() The segment
The segment ![]() meets
meets ![]() at point
at point ![]() and the line
and the line ![]() meets
meets ![]() at
at ![]() and
and ![]()
Prove that one of angles ![]() and
and ![]() is right. (Kukharchuk)
is right. (Kukharchuk)
Proof
![]() is the semiperimeter of
is the semiperimeter of ![]() and
and ![]()
![]() is the common side of these triangles, so
is the common side of these triangles, so ![]()
There is the circle ![]() inscribed in quadrilateral with diagonal
inscribed in quadrilateral with diagonal ![]() https://en.wikipedia.org/wiki/Tangential_quadrilateral
https://en.wikipedia.org/wiki/Tangential_quadrilateral
Let ![]() and
and ![]() be the centers and the radii of
be the centers and the radii of ![]() and
and ![]() be the Internal Similitude Center of circles
be the Internal Similitude Center of circles ![]() and
and ![]() so
so ![]()
WLOG, ![]() and lines
and lines ![]() and
and ![]() are the common internal tangents of
are the common internal tangents of ![]() and
and ![]() so point
so point ![]() is the Internal Similitude Center of circles
is the Internal Similitude Center of circles ![]() and
and ![]()
Lines ![]() and
and ![]() are the common external tangents of
are the common external tangents of ![]() and
and ![]() so point
so point ![]() is the External Similitude Center of circles
is the External Similitude Center of circles ![]() and
and ![]() therefore, points
therefore, points ![]() and
and ![]() are collinear ( Monge's theorem for centers).
are collinear ( Monge's theorem for centers).
In accordance with Lemma, ![]()
Lemma
Let circles ![]() and
and ![]() centered at
centered at ![]() and
and ![]() with radii
with radii ![]() and
and ![]() are internally tangent line
are internally tangent line ![]() at point
at point ![]() Point
Point ![]() lies at segment
lies at segment ![]() such that
such that ![]() Segment
Segment ![]()
![]() contains
contains ![]()
Prove that ![]()
Proof
Let ![]() be the point on
be the point on ![]() opposite
opposite ![]()
![]()
Homothety centered at ![]() with ratio
with ratio ![]() sends point
sends point ![]() to point
to point ![]() at
at ![]() So radius
So radius ![]() maps to radius
maps to radius ![]() which means
which means ![]() maps to
maps to ![]()
Point ![]() maps to point
maps to point ![]() Denote
Denote ![]()
Then ![]()
![]()
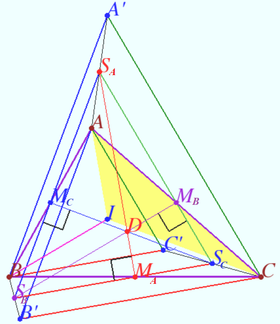
2025 I Problem 19
Let ![]() be the incenter of a triangle
be the incenter of a triangle ![]() be the orthocenters of the triangles
be the orthocenters of the triangles ![]()
![]() be the midpoints of
be the midpoints of ![]() and
and ![]() be the midpoints of
be the midpoints of ![]()
Prove that ![]() are concurrent. (Kuznetsov)
are concurrent. (Kuznetsov)
Proof
![]() is the orthocenters of
is the orthocenters of ![]()
Similarly, ![]()
![]()
![]()
![]() is the midline of trapezium
is the midline of trapezium ![]()
![]()
Denote B-excenter of ![]() as
as ![]() and
and ![]() the foots from
the foots from ![]() and
and ![]() to
to ![]()
![]()
![]()
![]()
![]()
![]() Similarly,
Similarly, ![]()
Therefore ![]() are the heights of
are the heights of ![]() which are crossed at the orthocenter of this triangle.
which are crossed at the orthocenter of this triangle.
2025 I Problem 20
Let ![]() be the orthocenter of a triangle
be the orthocenter of a triangle ![]() and
and ![]() be the midpoints of segments
be the midpoints of segments ![]() respectively. The perpendicular from
respectively. The perpendicular from ![]() to
to ![]() meets
meets ![]() at point
at point ![]() Points
Points ![]() and
and ![]() are defined similarly.
are defined similarly.
Prove that points ![]() and
and ![]() are collinear. (Ivlev)
are collinear. (Ivlev)
Proof
![]() is a diameter of the nine-point circle
is a diameter of the nine-point circle ![]() so the projection of
so the projection of ![]() onto
onto ![]() point
point ![]() lies on
lies on ![]() The foot of perpendicular from
The foot of perpendicular from ![]() to
to ![]() point
point ![]() lies on
lies on ![]()
Therefore lines ![]() and
and ![]() crosses at point
crosses at point ![]() lies on the polar
lies on the polar ![]() with respect
with respect ![]()
Similarly ![]() and
and ![]() also lie on this polar.
also lie on this polar.![]()
Proof 2
Denote ![]() the circumcenter of
the circumcenter of ![]()
![]()
![]() WLOG
WLOG ![]()
It is known that raduis ![]()
![]()
![]()
![]() and
and ![]() are the heights of
are the heights of ![]()
![]()
![]()
Therefore, ![]() is the tangent
is the tangent ![]()
Let ![]() be the circle centered at
be the circle centered at ![]() with zero radius.
with zero radius. ![]() is the radical axis of
is the radical axis of ![]() and
and ![]() is the radical axis of
is the radical axis of ![]() and
and ![]() so
so ![]() is the radical center of
is the radical center of ![]() and
and ![]()
![]() lies on radical axis of
lies on radical axis of ![]() and
and ![]() Similarly,
Similarly, ![]() and
and ![]() lies on this radical axis.
lies on this radical axis.![]()
vladimir.shelomovskii@gmail.com, vvsss
2025 I Problem 21
Let ![]() be a point inside a quadrilateral
be a point inside a quadrilateral ![]() such that
such that ![]() Points
Points ![]() are isogonally conjugated to
are isogonally conjugated to ![]() with respect to the triangles
with respect to the triangles ![]() respectively.
respectively.
Prove that the diagonals of the quadrilaterals ![]() and
and ![]() concur. (Galyapin)
concur. (Galyapin)
Proof
Denote ![]() By applying the Law of Sines on
By applying the Law of Sines on ![]() and
and ![]() we get:
we get:
![]()
![]()
![]() there is the point
there is the point ![]() isogonally conjugated to
isogonally conjugated to ![]() with respect to quadrilateral
with respect to quadrilateral ![]()
The lines ![]() and
and ![]() are isogonally conjugated to
are isogonally conjugated to ![]() with respect to
with respect to ![]() so points
so points ![]() and
and ![]() are collinear.
are collinear.
Similarly points ![]() and
and ![]() are collinear.
are collinear.
Point ![]() isogonally conjugated to
isogonally conjugated to ![]() with respect to
with respect to ![]()
Point ![]() isogonally conjugated to
isogonally conjugated to ![]() with respect to
with respect to ![]()
Adding last two equations we get ![]() Similarly
Similarly ![]()
![]()
By applying the Law of Sines on ![]() and
and ![]() we get:
we get: ![]()
By applying the Law of Sines on ![]() and
and ![]() we get:
we get: ![]()
![]()
![]() According Menelaus theorem, points
According Menelaus theorem, points ![]() and
and ![]() are collinear.
are collinear.
Similarly, points ![]() and
and ![]() are collinear.
are collinear.![]()
2025 I Problem 22
Let a circle ![]() and an ellipse with foci
and an ellipse with foci ![]() inside it be given. Construct a chord
inside it be given. Construct a chord ![]() of the circle touching the ellipse such that
of the circle touching the ellipse such that ![]() is a cyclic quadrilateral.
is a cyclic quadrilateral.
Proof
Denote ![]() and
and ![]() the crosspoints of
the crosspoints of ![]() and line
and line ![]()
Let ![]() be the point with propertyes
be the point with propertyes ![]() To construct this point one can construct any circle through the points
To construct this point one can construct any circle through the points ![]() and
and ![]() and intersecting
and intersecting ![]() The desired point is the intersection of the radical axis of these circles (common chord line) and the line
The desired point is the intersection of the radical axis of these circles (common chord line) and the line ![]() .
.
Let ![]() be the circumscribed circle of given ellipse.
be the circumscribed circle of given ellipse.
Let ![]() be the inverse of a point
be the inverse of a point ![]() with respect to
with respect to ![]()
Let ![]() be the point of the ellipse such that
be the point of the ellipse such that ![]() and
and ![]() be
the crosspoints of
be
the crosspoints of ![]() and
and ![]()
Then ![]() is tangent to the ellipse and
is tangent to the ellipse and ![]() is a cyclic quadrilateral.
(See Ellipse and tangent)
is a cyclic quadrilateral.
(See Ellipse and tangent)
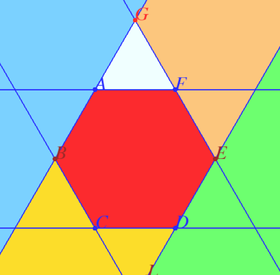
2025 I Problem 23
Let us say that a subset points ![]() of the plane contains a hole if there exists a disc not contained in
of the plane contains a hole if there exists a disc not contained in ![]() but contained inside some polygon with the boundary lying in
but contained inside some polygon with the boundary lying in ![]() Can the plane be presented as a union of
Can the plane be presented as a union of ![]() convex sets such that the union of any
convex sets such that the union of any ![]() from them contains a hole? (Spivak)
from them contains a hole? (Spivak)
Solution
Let ![]() The first element of the desired set is a regular hexagon
The first element of the desired set is a regular hexagon ![]() and the remaining six are half-planes adjacent to its edges external for hexagon.
and the remaining six are half-planes adjacent to its edges external for hexagon.
It is clear that the last six has a hole which is a hexagon, and for any other group the hole is a regular triangle adjacent to the hexagon ![]() for half-plane
for half-plane ![]()
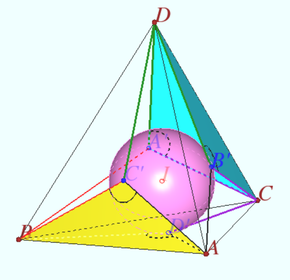
2025 I Problem 24
The insphere of a tetrahedron ![]() touches the faces
touches the faces ![]() at points
at points ![]() respectively. Denote by
respectively. Denote by ![]() the area of the triangle
the area of the triangle ![]()
Prove that there exists a triangle with sidelengths
![]()
Proof
Let us consider the net of the tetrahedron ![]() onto a plane
onto a plane ![]() There is three points
There is three points ![]() belonging faces
belonging faces ![]() and
and ![]() Denote
Denote ![]()
![]()
Tangents from each vertex are equals
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Similarly ![]()
Therefore three sidelength are proportional to ![]()
Let us place three points ![]() in the unit circle, the angles between which are equal to
in the unit circle, the angles between which are equal to
![]() Then the lengths of the chords are equal to
Then the lengths of the chords are equal to ![]()
So the required triangle is constructed.![]()
Proof
Proof
2024 II Problem 6
A point ![]() lies on one of medians of triangle
lies on one of medians of triangle ![]() in such a way that
in such a way that ![]() Prove that there exists a point
Prove that there exists a point ![]() on another median such that
on another median such that ![]() (A.Zaslavsky)
(A.Zaslavsky)
Proof
1. Denote ![]() It is known that barycentric coordinates are
It is known that barycentric coordinates are
![]()
2. Denote ![]()
![]() is tangent to
is tangent to ![]()
![]() is tangent
is tangent ![]()
![]() is the radical axes of
is the radical axes of ![]() and
and ![]() the power of a point
the power of a point ![]() with respect to a circle
with respect to a circle ![]() is
is ![]() so the power of a point
so the power of a point ![]() with respect to a circle
with respect to a circle ![]() is
is ![]()
![]() so
so ![]() is tangent to
is tangent to ![]()
![]() so point
so point ![]() symmetrical to
symmetrical to ![]() with respect to the
with respect to the ![]() median satisfies the conditions.
median satisfies the conditions. ![]()
2024 II Problem 2(8)
Let ![]() be the midpoint of side
be the midpoint of side ![]() of an acute-angled triangle
of an acute-angled triangle ![]() and
and ![]() be the projection of the orthocenter
be the projection of the orthocenter ![]() to the bisector of angle
to the bisector of angle ![]() Prove that
Prove that ![]() bisects the segment
bisects the segment ![]() (L.Emelyanov)
(L.Emelyanov)
Solution
Denote ![]() - the midpoint of
- the midpoint of ![]() and
and ![]() the foots of the heights,
the foots of the heights, ![]() be the Euler circle
be the Euler circle ![]()
![]() is the circle
is the circle ![]() with the diameter
with the diameter ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() points
points ![]() and
and ![]() are collinear.
are collinear.
2024 II Problem 4(8)
A square with sidelength ![]() is cut from the paper. Construct a segment with length
is cut from the paper. Construct a segment with length ![]() using at most
using at most ![]() folds. No instruments are available, it is allowed only to fold the paper and to mark the common points of folding lines. (M.Evdokimov)
folds. No instruments are available, it is allowed only to fold the paper and to mark the common points of folding lines. (M.Evdokimov)
Solution
Main idea: ![]()
![]()
![]() Let
Let ![]()
![]() We perform
We perform ![]() horizontal fold of the sheet. We get line
horizontal fold of the sheet. We get line ![]() We perform
We perform
![]() vertical folds of the sheet. We get
vertical folds of the sheet. We get ![]() vertical lines at a distance of
vertical lines at a distance of ![]() from each other.
from each other.
Point ![]() is the lower left corner of the sheet, point
is the lower left corner of the sheet, point ![]() is the lower point of the second vertical line, point
is the lower point of the second vertical line, point ![]() is the lower point of the
is the lower point of the ![]() line, point
line, point ![]() is the point at the intersection of the horizontal line and the
is the point at the intersection of the horizontal line and the ![]() vertical line.
vertical line.
Points ![]() and
and ![]() are at the intersection of the lines
are at the intersection of the lines ![]() and
and ![]() and the
and the ![]() vertical line.
vertical line.
2024 II Problem 3(9)
Let ![]() and
and ![]() be two pairs of points isogonally conjugated with respect to a triangle
be two pairs of points isogonally conjugated with respect to a triangle ![]() and
and ![]() be the common point of lines
be the common point of lines ![]() and
and ![]() Prove that the pedal circles of points
Prove that the pedal circles of points ![]() and
and ![]() are coaxial. (L.Shatunov, V.Shelomovskii)
are coaxial. (L.Shatunov, V.Shelomovskii)
Solution
1. Let ![]() be the isogonal conjugate of a point
be the isogonal conjugate of a point ![]() with respect to a triangle
with respect to a triangle ![]() Then circle centered at the midpoint
Then circle centered at the midpoint ![]() is the common pedal circle of points
is the common pedal circle of points ![]() and
and ![]() ( Circumcircle of pedal triangles) So center
( Circumcircle of pedal triangles) So center ![]() is the midpoint
is the midpoint ![]() and center
and center ![]() is the midpoint
is the midpoint ![]()
2. Denote ![]() Then
Then ![]() is the isogonal conjugate of a point
is the isogonal conjugate of a point ![]() with respect to
with respect to ![]() So center
So center ![]() is the midpoint
is the midpoint ![]() ( Two pares of isogonally conjugate points)
( Two pares of isogonally conjugate points)
3. The Gauss line (or Gauss–Newton line) is the line joining the midpoints of the three diagonals of a complete quadrilateral ![]() (Gauss line).So points
(Gauss line).So points ![]() and
and ![]() are collinear as was to be proven.
are collinear as was to be proven. ![]()
2024 II Problem 4(9)
For which ![]() it is possible to mark several different points and several different circles on the plane in such a way that:
it is possible to mark several different points and several different circles on the plane in such a way that:
- exactly ![]() marked circles pass through each marked point;
marked circles pass through each marked point;
- exactly ![]() marked points lie on each marked circle;
marked points lie on each marked circle;
- the center of each marked circle is marked? (P.Puchkov)
Solution
Case ![]() Circles centered at
Circles centered at ![]() and
and ![]() with radii
with radii ![]()
Case ![]() is not paralel to
is not paralel to ![]()
Four circles are centered at points ![]() and
and ![]() Each radius is equal
Each radius is equal ![]()
Case ![]() is not paralel to
is not paralel to ![]() or
or ![]()
Eight circles centered at ![]() and
and ![]() have radii
have radii ![]()
Case ![]()
Answer For all ![]()
2024 II Problem 5(9)
Let ![]() be an isosceles triangle
be an isosceles triangle ![]() be its circumcenter,
be its circumcenter,![]() be the orthocenter, and
be the orthocenter, and ![]() be a point inside the triangle such that
be a point inside the triangle such that ![]()
Prove that ![]() (A.Zaslavsky)
(A.Zaslavsky)
Proof
Denote ![]() the midpoint
the midpoint ![]() the midpoint
the midpoint ![]() the foot from
the foot from ![]() to
to ![]() tangent to
tangent to ![]()
![]() There is a spiral similarity
There is a spiral similarity ![]() centered at point
centered at point ![]() that maps
that maps ![]() into
into ![]()
The coefficient of similarity ![]() rotation angle equal
rotation angle equal ![]()
![]()
![]()
![]() so
so ![]() is tangent to
is tangent to ![]() Basic information
Basic information
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Points
Points ![]() and
and ![]() are collinear, so
are collinear, so ![]() median of
median of ![]()
![]() is
is ![]() symmedian of
symmedian of ![]()
![]() is
is ![]() Humpty point.
Humpty point.
2024 II Problem 7(9)
Let triangle ![]() and point
and point ![]() on the side
on the side ![]() be given. Let
be given. Let ![]() be such point on the side
be such point on the side ![]() that
that ![]() The cross points of segments
The cross points of segments ![]() and
and ![]() with the incircle
with the incircle ![]() of
of ![]() form a convex quadrilateral
form a convex quadrilateral ![]()
Find the locus of crosspoints of diagonals ![]() (D.Brodsky)
(D.Brodsky)
Solution 1. Particular case of Fixed point .
2. Denote ![]()
![]()
![]() We perform simple transformations and get:
We perform simple transformations and get:
![]() We use Stewart's theorem and get:
We use Stewart's theorem and get:
![]()
![]()
![]() Similarly
Similarly ![]() Therefore
Therefore ![]() not depends from
not depends from ![]()
Let ![]() be the midpoint of
be the midpoint of ![]() is the median of
is the median of ![]() and
and ![]()
The line ![]() cross the median of
cross the median of ![]() at point
at point ![]() such that
such that ![]()
So point ![]() is fixed and this point lyes on
is fixed and this point lyes on ![]() .
.
Therefore the locus of crosspoints of diagonals ![]() is point
is point ![]()
Corollary
Let line ![]() . Then
. Then ![]()
2024 II Problem 7(10)
Let ![]() be a triangle with
be a triangle with ![]() and
and ![]() be its bisectors,
be its bisectors, ![]() be the projections of
be the projections of ![]() to
to ![]() and
and ![]() respectively, and
respectively, and ![]() be the second common point of the circle
be the second common point of the circle ![]() with
with ![]()
Prove that points ![]() are collinear. (K.Belsky)
are collinear. (K.Belsky)
Proof
Denote ![]() the incenter of
the incenter of ![]()
![]() the midpoint of
the midpoint of ![]()
It is known ( Division of bisector) that
![]()
![]()
![]()
![]() is cyclic.
is cyclic.
Therefore ![]() is cyclic
is cyclic ![]()
Let ![]()
It is known that points ![]() and
and ![]() are collinear,
are collinear,
![]()
![]() is the diameter of
is the diameter of ![]()
![]()
![]()
![]() is the bisector of
is the bisector of ![]()
Bisector ![]()
Altitude ![]()
Note that the point ![]() is a Feuerbach point of
is a Feuerbach point of ![]() since both the inscribed circle and the Euler circle pass through it.
since both the inscribed circle and the Euler circle pass through it.
2024 I Problem 2
Three distinct collinear points are given. Construct the isosceles triangles such that these points are their circumcenter, incenter and excenter (in some order).
Solution
Let ![]() be the midpoint of the segment connecting the incenter and excenter. It is known that point
be the midpoint of the segment connecting the incenter and excenter. It is known that point ![]() belong the circumcircle.
Construction is possible if a circle with diameter IE (incenter – excenter) intersects a circle with radius OM (circumcenter – M). Situation when
belong the circumcircle.
Construction is possible if a circle with diameter IE (incenter – excenter) intersects a circle with radius OM (circumcenter – M). Situation when ![]() between
between ![]() and
and ![]() is impossible.
is impossible.
Denote points ![]() such that
such that ![]() and
and ![]()
Suppose point ![]() is circumcenter, so
is circumcenter, so ![]() is incenter.
is incenter. ![]() is midpoint BC. The vertices of the desired triangle are located at the intersection of a circle with center
is midpoint BC. The vertices of the desired triangle are located at the intersection of a circle with center ![]() and radius
and radius ![]() with
with ![]() and a line
and a line ![]()
Suppose point ![]() is circumcenter, so
is circumcenter, so ![]() is incenter.
is incenter. ![]() is midpoint
is midpoint ![]() The vertices of the desired triangle are located at the intersection of a circle with center
The vertices of the desired triangle are located at the intersection of a circle with center ![]() and radius
and radius ![]() with
with ![]() and a line
and a line ![]()
Suppose point ![]() is circumcenter, so
is circumcenter, so ![]() is incenter.
is incenter. ![]() is midpoint
is midpoint ![]() Suppose
Suppose ![]() The vertices of the desired triangle are located at the intersection of a circle with center
The vertices of the desired triangle are located at the intersection of a circle with center ![]() and radius
and radius ![]() with
with ![]() and a line
and a line ![]()
If ![]() there is not desired triangle.
there is not desired triangle.
2024 I Problem 8
Let ![]() be a quadrilateral with
be a quadrilateral with ![]() and
and ![]()
The incircle of ![]() touches the sides
touches the sides ![]() and
and ![]() at points
at points ![]() and
and ![]() respectively.
respectively.
The midpoints of segments ![]() and
and ![]() are points
are points ![]()
Prove that points ![]() are concyclic.
are concyclic.
Solution
![]()
![]()
![]()
![]() is the rotation of
is the rotation of ![]() around a point
around a point ![]() through an angle
through an angle ![]()
![]() is the rotation of
is the rotation of ![]() around a point
around a point ![]() through an angle
through an angle ![]()
So ![]() is the rotation of
is the rotation of ![]() around a point
around a point ![]() through an angle
through an angle ![]()
2024 I Problem 9
Let ![]() be a trapezoid circumscribed around a circle
be a trapezoid circumscribed around a circle ![]() centered at
centered at ![]() which touches the sides
which touches the sides ![]() and
and ![]() at points
at points ![]() respectively.
respectively.
The line passing trough ![]() and parallel to the bases of trapezoid meets
and parallel to the bases of trapezoid meets ![]() at point
at point ![]()
Prove that ![]() and
and ![]() concur.
concur.
Solution
Solution 1. ![]()
![]()
![]() is the center of similarity of triangles
is the center of similarity of triangles ![]() and
and ![]()
Solution 2. ![]()
Denote ![]()
![]()
![]()
2024 I Problem 12
The bisectors ![]() of a
of a ![]() with
with ![]() meet at point
meet at point ![]()
The circumcircles of triangles ![]() meet at point
meet at point ![]()
Prove that the line ![]() bisects the side
bisects the side ![]()
Proof
Denote ![]() the midpoint
the midpoint ![]()
![]()
![]() In triangles
In triangles ![]() and
and ![]() , by applying the law of sines, we get
, by applying the law of sines, we get
![]()
We use the formulas for circle ![]() and get
and get ![]()
![]() In triangles
In triangles ![]() and
and ![]() , by applying the law of sines, we get
, by applying the law of sines, we get
![]()
![]()
Therefore ![]() The function
The function ![]() increases monotonically on the interval
increases monotonically on the interval ![]()
This means ![]() and points
and points ![]() and
and ![]() are collinear.
are collinear.
2024 I Problem 14
The incircle ![]() of a right-angled triangle
of a right-angled triangle ![]() touches the circumcircle
touches the circumcircle ![]() of its medial triangle at point
of its medial triangle at point ![]() Let
Let ![]() be the tangent to
be the tangent to ![]() from the midpoint
from the midpoint ![]() of the hypothenuse
of the hypothenuse ![]() distinct from
distinct from ![]() Prove that
Prove that ![]()
Proof
Let ![]() and
and ![]() be the circumcircle and the incenter of
be the circumcircle and the incenter of ![]()
Let ![]() be nine-point center of
be nine-point center of ![]() be the point at
be the point at ![]() such that
such that ![]()
Denote ![]()
![]() is the right-angled triangle, so
is the right-angled triangle, so ![]() is the midpoint
is the midpoint ![]()
![]() Let
Let ![]() be the result of the homothety of the point
be the result of the homothety of the point ![]() centered in
centered in ![]() with the coefficient
with the coefficient ![]() Then
Then
![]()
![]()
![]() WLOG,
WLOG, ![]()
Let ![]() be the foot from
be the foot from ![]() to
to ![]() .
.
![]()
![]()
![]() Therefore points
Therefore points ![]() and
and ![]() are collinear.
are collinear.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
2024 I Problem 15
The difference of two angles of a triangle is greater than ![]() Prove that the ratio of its circumradius and inradius is greater than
Prove that the ratio of its circumradius and inradius is greater than ![]()
Proof
Suppose, ![]()
Let ![]() be the point on
be the point on ![]() opposite
opposite ![]() be the midpoint of arc
be the midpoint of arc ![]() Then
Then ![]()
![]()
![]()
![]()
![]()
![]() Incenter
Incenter ![]() triangle
triangle ![]() lies on
lies on ![]() therefore
therefore ![]()
We use the Euler law ![]()
If ![]() then
then ![]()
![]()
![]()
If ![]() increases so
increases so ![]() decreases.
decreases.
2024 I Problem 16
Let ![]() and
and ![]() be the bisectors of a triangle
be the bisectors of a triangle ![]()
The segments ![]() and
and ![]() meet at point
meet at point ![]() Let
Let ![]() be the projection of
be the projection of ![]() to
to ![]()
Points ![]() and
and ![]() on the sides
on the sides ![]() and
and ![]() respectively, are such that
respectively, are such that ![]()
Prove that ![]()
Proof
![]() is the common side)
is the common side) ![]()
![]() is the midpoint
is the midpoint ![]()
![]() is the midpoint of
is the midpoint of ![]()
![]() (see Division of bisector for details.)
(see Division of bisector for details.)
So ![]() Denote
Denote ![]()
![]()
![]()
Another solution see 2024_Sharygin_olimpiad_Problem_16
2024 I Problem 17
Let ![]() be not isosceles triangle,
be not isosceles triangle, ![]() be its incircle.
be its incircle.
Let ![]() and
and ![]() be the points at which the incircle of
be the points at which the incircle of ![]() touches the sides
touches the sides ![]() and
and ![]() respectively.
respectively.
Let ![]() be the point on ray
be the point on ray ![]() such that
such that ![]()
Let ![]() be the point on ray
be the point on ray ![]() such that
such that ![]()
The circumcircles of ![]() and
and ![]() intersect
intersect ![]() again at
again at ![]() and
and ![]() respectively.
respectively.
Prove that ![]() and
and ![]() are concurrent.
are concurrent.
Proof
![]() so points
so points ![]() and
and ![]() are collinear (see Symmetry and incircle for details).
are collinear (see Symmetry and incircle for details).
Therefore lines ![]() and
and ![]() are concurrent (see Symmetry and incircle A for details.)
are concurrent (see Symmetry and incircle A for details.)
2024 I Problem 18
Let ![]() be the altitudes of an acute-angled triangle
be the altitudes of an acute-angled triangle ![]() be its excenter corresponding to
be its excenter corresponding to ![]() be the reflection of
be the reflection of ![]() about the line
about the line ![]() Points
Points ![]() are defined similarly. Prove that the lines
are defined similarly. Prove that the lines ![]() concur.
concur.
Proof
Denote ![]() the incenter of
the incenter of ![]() Points
Points ![]() are collinear.
We will prove that
are collinear.
We will prove that ![]() Denote
Denote ![]()
![]()
![]() - semiperimeter.
- semiperimeter.
![]() The area
The area ![]()
![]()
![]() Points
Points ![]() are collinear, so the lines
are collinear, so the lines ![]() concur at the point
concur at the point ![]()
2024 I Problem 19
A triangle ![]() its circumcircle
its circumcircle ![]() , and its incenter
, and its incenter ![]() are drawn on the plane.
are drawn on the plane.
Construct the circumcenter ![]() of
of ![]() using only a ruler.
using only a ruler.
Solution
We successively construct:
- the midpoint ![]() of the arc
of the arc ![]()
- the midpoint ![]() of the arc
of the arc ![]()
- the polar ![]() of point
of point ![]()
- the polar ![]() of point
of point ![]()
- the polar ![]() of the line
of the line ![]()
- the tangent ![]() to
to ![]()
- the tangent ![]() to
to ![]()
- the trapezium ![]()
- the point ![]()
- the point ![]()
- the midpoint ![]() of the segment
of the segment ![]()
- the midpoint ![]() of the segment
of the segment ![]()
- the diameter ![]() of
of ![]()
- the diameter ![]() of
of ![]()
- the circumcenter ![]()
2024 I Problem 20
Let a triangle ![]() points
points ![]() and
and ![]() be given,
be given, ![]() Points
Points ![]() and
and ![]() are the isogonal conjugate of the points
are the isogonal conjugate of the points ![]() and
and ![]() respectively, with respect to
respectively, with respect to ![]()
Denote ![]() and
and ![]() the circumradii of triangles
the circumradii of triangles ![]() and
and ![]() respectively.
respectively.
Prove that ![]() where
where ![]() is the area of
is the area of ![]()
Proof
Denote ![]()
![]()
![]() It is easy to prove that
It is easy to prove that
![]() is equivalent to
is equivalent to ![]()
![]()
![]() By applying the law of sines, we get
By applying the law of sines, we get
![]()
![]()
![]()
![]() We need to prove that
We need to prove that
![]() We make the transformations:
We make the transformations:
![]()
![]()
![]()
![]()
![]()
![]()
![]() The last statement is obvious.
The last statement is obvious.
2024 I Problem 21
A chord ![]() of the circumcircle of a triangle
of the circumcircle of a triangle ![]() meets the sides
meets the sides ![]() at points
at points ![]() respectively. The tangents to the circumcircle at
respectively. The tangents to the circumcircle at ![]() and
and ![]() meet at point
meet at point ![]() and the tangents at points
and the tangents at points ![]() and
and ![]() meets at point
meets at point ![]() The line
The line ![]() meets
meets ![]() at point
at point ![]()
Prove that the lines ![]() and
and ![]() concur.
concur.
Proof
WLOG, ![]() Denote
Denote ![]()
Point ![]() is inside
is inside ![]()
We use Pascal’s theorem for quadrilateral ![]() and get
and get ![]()
We use projective transformation which maps ![]() to a circle and that maps the point
to a circle and that maps the point ![]() to its center.
to its center.
From this point we use the same letters for the results of mapping. Therefore the segments ![]() and
and ![]() are the diameters of
are the diameters of ![]() is the midpoint
is the midpoint ![]()
![]()
preimage ![]() lies on preimage
lies on preimage ![]()
2024 I Problem 22
A segment ![]() is given. Let
is given. Let ![]() be an arbitrary point of the perpendicular bisector to
be an arbitrary point of the perpendicular bisector to ![]()
![]() be the point on the circumcircle of
be the point on the circumcircle of ![]() opposite to
opposite to ![]() and an ellipse centered at
and an ellipse centered at ![]() touche
touche ![]()
Find the locus of touching points ![]() of the ellipse with the line
of the ellipse with the line ![]()
Solution
Denote ![]() the midpoint
the midpoint ![]() the point on the line
the point on the line ![]()
![]()
![]()
![]()
![]() In order to find the ordinate of point
In order to find the ordinate of point ![]() we perform an affine transformation (compression along axis
we perform an affine transformation (compression along axis ![]() which will transform the ellipse
which will transform the ellipse ![]() into a circle with diameter
into a circle with diameter ![]() The tangent of the
The tangent of the ![]() maps into the tangent of the
maps into the tangent of the ![]()
![]()
![]()
![]()
![]() Denote
Denote ![]()
So point ![]() is the fixed point (
is the fixed point (![]() not depends from angle
not depends from angle ![]()
Therefore point ![]() lies on the circle with diameter
lies on the circle with diameter ![]() (except points
(except points ![]() and
and ![]()
One-to-one mapping of the circle
Let a circle ![]() two fixed points
two fixed points ![]() and
and ![]() on it and a point
on it and a point ![]() inside it be given.
Then there is a one-to-one mapping of the circle
inside it be given.
Then there is a one-to-one mapping of the circle ![]() onto itself, based on the following two theorems.
onto itself, based on the following two theorems.
1. Let a circle ![]() two fixed points
two fixed points ![]() and
and ![]() on
on ![]() and a point
and a point ![]() inside
inside ![]() be given.
be given.
Let an arbitrary point ![]() be given.
be given.
Let ![]() is the midpoint of the arc
is the midpoint of the arc ![]()
Denote ![]() Prove that
Prove that ![]()
2. Let a circle ![]() two fixed points
two fixed points ![]() and
and ![]() on
on ![]() and a point
and a point ![]() inside
inside ![]() be given.
be given.
Let an arbitrary point ![]() be given.
be given.
Let ![]() is the midpoint of the arc
is the midpoint of the arc ![]()
Denote ![]()
Denote ![]() Prove that
Prove that ![]()
Proof
![]()
Points ![]() are collinear.
are collinear.
![]()
![]()
2. Points ![]() and
and ![]() are collinear (see Claim in 2024, Problem 23).
are collinear (see Claim in 2024, Problem 23).
We use Pascal's theorem for points ![]() and crosspoints
and crosspoints ![]() and get
and get ![]()
2024 I Problem 23
A point ![]() moves along a circle
moves along a circle ![]() Let
Let ![]() and
and ![]() be fixed points of
be fixed points of ![]() and
and ![]() be an arbitrary point inside
be an arbitrary point inside ![]()
The common external tangents to the circumcircles of triangles ![]() and
and ![]() meet at point
meet at point ![]()
Prove that all points ![]() lie on two fixed lines.
lie on two fixed lines.
Solution
Denote ![]()
![]()
![]() is the circumcenter of
is the circumcenter of ![]() is the circumcenter of
is the circumcenter of ![]()
Let ![]() and
and ![]() be the midpoints of the arcs
be the midpoints of the arcs ![]() of
of ![]()
Let ![]() and
and ![]() be the midpoints of the arcs
be the midpoints of the arcs ![]() of
of ![]()
These points not depends from position of point ![]()
Suppose, ![]() see diagram).
see diagram).
![]()
![]() Let
Let ![]()
![]() Similarly,
Similarly, ![]()
Let ![]()
Therefore ![]() Similarly, if
Similarly, if ![]() then
then ![]()
Claim
Points ![]() and
and ![]() are collinear.
are collinear.
Proof
![]() is the midpoint of arc
is the midpoint of arc ![]() Denote
Denote ![]()
![]()
![]()
![]() Therefore
Therefore ![]() points
points ![]() and
and ![]() are collinear.
are collinear.
The problem from MGTU
The lateral face of the regular triangular pyramid ![]() is inclined to the plane of the base
is inclined to the plane of the base ![]() at an angle of
at an angle of ![]() Points
Points ![]() are the midpoints of the sides of the
are the midpoints of the sides of the ![]() Triangle
Triangle ![]() is the lower base of a right prism. The edges of the upper base of the prism intersect the lateral edges of the pyramid
is the lower base of a right prism. The edges of the upper base of the prism intersect the lateral edges of the pyramid ![]() at points
at points ![]() The area of the total surface of the polyhedron with vertices
The area of the total surface of the polyhedron with vertices ![]() is equal to
is equal to ![]() Find the side of
Find the side of ![]()
Solution
Denote ![]() is the center of
is the center of ![]()
![]()
![]()
![]() The area of the total surface of the polyhedron with vertices
The area of the total surface of the polyhedron with vertices ![]() is
is
![]()
![]()
![]()
![]()
![]()
![]()
The trapezoid problem from MGTU
Points ![]() and
and ![]() are the midpoints of bases
are the midpoints of bases ![]() and
and ![]() of trapezoid
of trapezoid ![]()
Denote ![]() the angle between lines
the angle between lines ![]() and
and ![]()
Find the area of trapezoid ![]() if
if ![]()
Solution
![]()
![]() By applying the Law of Cosines on
By applying the Law of Cosines on ![]() we get
we get
![]()
![]()