Difference between revisions of "Hook Length Theorem"
(hook number for upper right squares are wrong not 1,1,1 its 3,2,1) |
|||
| Line 12: | Line 12: | ||
=Theorem= | =Theorem= | ||
| − | Let the number of | + | Let the number of cells in a Young tableau be n. Define a hook length of a block to be the number of blocks to the right and below the block, including the block. In the below image, the hook of the red square is <math>7</math>. |
[[File:Hook Example.png|200px|center]] | [[File:Hook Example.png|200px|center]] | ||
| − | Let the product of all the | + | Let the product of all the hook lengths be <math>h</math>. Then the number of possible standard Young tableaux is <math>\frac{n!}{h}</math>. |
| + | |||
| + | |||
| + | The number of hooks of each block in the example tableau is shown below. | ||
[[File:TableauHook.png|200px|center]] | [[File:TableauHook.png|200px|center]] | ||
So in the example, the number of SYTs is <math>\frac{13!}{9\times7\times6\times3\times2\times1\times5\times3\times2\times4\times2\times1\times1} = 11440</math>. | So in the example, the number of SYTs is <math>\frac{13!}{9\times7\times6\times3\times2\times1\times5\times3\times2\times4\times2\times1\times1} = 11440</math>. | ||
| + | |||
| + | =Problem= | ||
| + | 2016 USAMO P2 | ||
Latest revision as of 11:21, 6 August 2025
Introduction
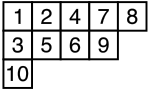
The hook length theorem is a theorem to be used on Standard Young Tableau. A standard Young Tableau is essentially a pack of blocks together, such as this one:
A tableau has a decreasing(not strictly decreasing) number of blocks in every row.
A Standard Young Tableau(SYT) has increasing numbers in both rows and columns. As shown in the figure, 1-3-10 is increasing, as well as 2-5, 4-6, 7-9, 1-2-4-7-8, and 3-5-6-9.
Theorem
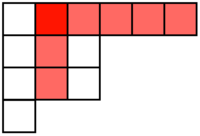
Let the number of cells in a Young tableau be n. Define a hook length of a block to be the number of blocks to the right and below the block, including the block. In the below image, the hook of the red square is 
.
Let the product of all the hook lengths be 
. Then the number of possible standard Young tableaux is 
.
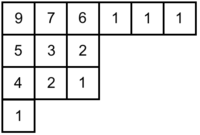
The number of hooks of each block in the example tableau is shown below.
So in the example, the number of SYTs is 
.
Problem
2016 USAMO P2
