Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2003 AMC 12B Problems/Problem 21"

m
(→‎Solution 3 (Geometric Probability))
 
Line 44: Line 44:
  
 
~PeterDoesPhysics
 
~PeterDoesPhysics
 +
==Solution 4 (Triangle Inequality)==
 +
 +
 +
Note that we can treat <math>\text{ABC}</math> as a triangle with side lengths <math>5</math>, <math>8</math> and <math>AC=x.</math> Because <math>0</math> and <math>\pi</math> are not pat of the interval of valid <math>\alpha</math> values, <math>\triangle \text{ABC}</math> is a non-degenerate triangle. Then, by the Triangle Inequality, <math>5+8>x,</math> <math>5+x>8,</math> and <math>8+x>5.</math> These reduce to <math>x<13,</math> <math>x>3,</math> and <math>x>-3.</math> Thus, the possible values of x are <math>3<x<13,</math> or <math>x=\text{[}4,5,6,7,8,9,10,11,12\text{]}.</math> Of these <math>9</math> possible <math>x,</math> <math>3</math> of them are less than <math>7,</math> so the probability that <math>x<7</math> is <math>\frac39=\frac13=\boxed{\text{(D)}}.</math>
 +
 +
 +
~~AndrewZhong2012~~
  
 
== See also ==
 
== See also ==

Latest revision as of 10:01, 8 August 2025

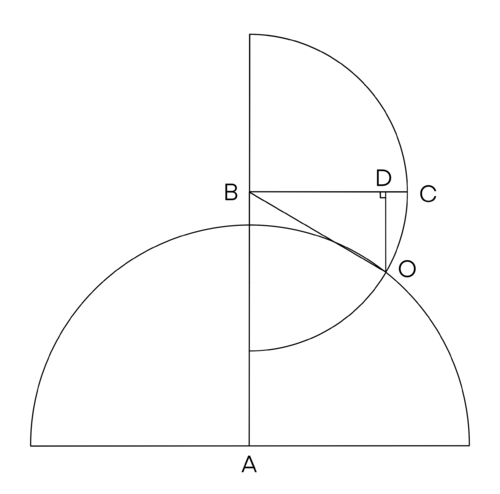
Problem

An object moves $8$ cm in a straight line from $A$ to $B$, turns at an angle $\alpha$, measured in radians and chosen at random from the interval $(0,\pi)$, and moves $5$ cm in a straight line to $C$. What is the probability that $AC < 7$?

$\mathrm{(A)}\ \frac{1}{6} \qquad\mathrm{(B)}\ \frac{1}{5} \qquad\mathrm{(C)}\ \frac{1}{4} \qquad\mathrm{(D)}\ \frac{1}{3} \qquad\mathrm{(E)}\ \frac{1}{2}$

Solution 1 (Trigonometry)

By the Law of Cosines, \begin{align*} AB^2 + BC^2 - 2 AB \cdot BC \cos \alpha = 89 - 80 \cos \alpha = AC^2 &< 49\\ \cos \alpha &> \frac 12\\ \end{align*}

It follows that $0 < \alpha < \frac {\pi}3$, and the probability is $\frac{\pi/3}{\pi} = \boxed{\textbf{(D) } \frac13 }$.

Solution 2 (Analytic Geometry)

2003AMC12BP21.png

$WLOG$, let the object turn clockwise.

Let $B = (0, 0)$, $A = (0, -8)$.

Note that the possible points of $C$ create a semi-circle of radius $5$ and center $B$. The area where $AC < 7$ is enclosed by a circle of radius $7$ and center $A$. The probability that $AC < 7$ is $\frac{\angle ABO}{180 ^\circ}$.

The function of $\odot B$ is $x^2 + y^2 = 25$, the function of $\odot A$ is $x^2 + (y+8)^2 = 49$.

$O$ is the point that satisfies the system of equations: $\begin{cases} x^2 + y^2 = 25 \\ x^2 + (y+8)^2 = 49 \end{cases}$

$x^2 + (y+8)^2 - x^2 - y^2 = 49 - 25$, $64 + 16y =24$, $y = - \frac52$, $x = \frac{5 \sqrt{3}}{2}$, $O = (\frac{5 \sqrt{3}}{2}, - \frac52)$

Note that $\triangle BDO$ is a $30-60-90$ triangle, as $BO = 5$, $BD = \frac{5 \sqrt{3}}{2}$, $DO = \frac52$. As a result $\angle CBO = 30 ^\circ$, $\angle ABO = 60 ^\circ$.

Therefore the probability that $AC < 7$ is $\frac{\angle ABO}{180 ^\circ} = \frac{60 ^\circ}{180 ^\circ} = \boxed{\textbf{(D) } \frac13 }$

~isabelchen

Solution 3 (Geometric Probability)

Setting $A = (0,0)$ we get that $B = (8,0)$, after assuming segment AB to be straight in the x-direction relative to our coordinate system (in other words, due to symmetrically we can set $x = 8$ for point B). This gives $C = (8 + 5cos(\alpha), 5sin(\alpha))$. Using the distance formula we get $sqrt((8 + 5cos(\alpha))^2 + (5sin(\alpha))^2) < 7$. After algebra, this simplifies to $cos(\alpha) < -\frac{1}{2}$. After evaluating the constraints of the problem, we land on option (D).

~PeterDoesPhysics

Solution 4 (Triangle Inequality)

Note that we can treat $\text{ABC}$ as a triangle with side lengths $5$, $8$ and $AC=x.$ Because $0$ and $\pi$ are not pat of the interval of valid $\alpha$ values, $\triangle \text{ABC}$ is a non-degenerate triangle. Then, by the Triangle Inequality, $5+8>x,$ $5+x>8,$ and $8+x>5.$ These reduce to $x<13,$ $x>3,$ and $x>-3.$ Thus, the possible values of x are $3<x<13,$ or $x=\text{[}4,5,6,7,8,9,10,11,12\text{]}.$ Of these $9$ possible $x,$ $3$ of them are less than $7,$ so the probability that $x<7$ is $\frac39=\frac13=\boxed{\text{(D)}}.$


~~AndrewZhong2012~~

See also

2003 AMC 12B (Problems • Answer Key • Resources)
Preceded by
Problem 20 		Followed by
Problem 22
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. AMC Logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2003_AMC_12B_Problems/Problem_21&oldid=256786"