Difference between revisions of "2020 USAMO Problems/Problem 1"

Latest revision as of 13:42, 1 September 2025

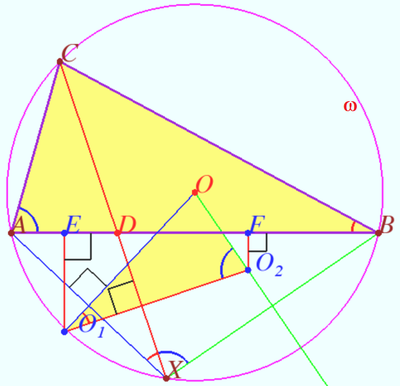
Problem 1

Let $ABC$ be a fixed acute triangle inscribed in a circle $\omega$ with center $O$ . A variable point $X$ is chosen on minor arc $AB$ of $\omega$ , and segments $CX$ and $AB$ meet at $D$ . Denote by $O_1$ and $O_2$ the circumcenters of triangles $ADX$ and $BDX$ , respectively. Determine all points $X$ for which the area of triangle $OO_1O_2$ is minimized.

Solution

Let $E$ be midpoint $AD.$ Let $F$ be midpoint $BD \implies$ $EF = ED + FD = \frac {AD}{2} + \frac {BD}{2} = \frac {AB}{2}.$ $E$ and $F$ are the bases of perpendiculars dropped from $O_1$ and $O_2,$ respectively.

Therefore $O_1O_2 \ge EF = \frac {AB}{2}.$

$CX \perp O_1O_2, AX \perp O_1O \implies \angle O O_1O_2 = \angle AXC$ $\angle AXC = \angle ABC (AXBC$ is cyclic) $\implies \angle O O_1O_2 = \angle ABC.$

Similarly $\angle BAC = \angle O O_2 O_1 \implies \triangle ABC \sim \triangle O_2 O_1O.$

The area of $\triangle OO_1O_2$ is minimized if $CX \perp AB$ because $\frac {[OO_1O_2]} {[ABC]} = \left(\frac {O_1 O_2} {AB}\right)^2 \ge \left(\frac {EF} {AB}\right)^2 = \frac {1}{4}.$ vladimir.shelomovskii@gmail.com, vvsss

Video Solution 1

https://www.youtube.com/watch?v=m157cfw0vdE

Video Solution 2

https://youtube.com/watch?v=HLNb_4KmayA

@@ Line 21: / Line 21: @@
 '''vladimir.shelomovskii@gmail.com, vvsss'''
-==Video Solution==
+==Video Solution 1==
 https://www.youtube.com/watch?v=m157cfw0vdE
+==Video Solution 2==
+https://youtube.com/watch?v=HLNb_4KmayA
+==See also==
+{{USAMO newbox|year=2020|before=First Problem|num-a=2}}
 {{MAA Notice}}

2020 USAMO (Problems • Resources)
Preceded by First Problem	Followed by Problem 2
1 • 2 • 3 • 4 • 5 • 6
All USAMO Problems and Solutions

Page

Toolbox

Search