Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2012 AIME II Problems/Problem 9"

(→‎Solution 4)
(→‎Solution 5)
Line 97: Line 97:
  
 
==Solution 5==
 
==Solution 5==
−
We can calculate the first term <math>\frac{sin 2x}{sin 2y} = \frac{2 sin x cos x}{2 sin y cos y} = 3 \cdot \frac{1}{2} = \frac{3}{2}.</math>
+
We can calculate the first term <math>\frac{\sin 2x}{\sin 2y} = \frac{2 \sin x \cos x}{2 \sin y \cos y} = 3 \cdot \frac{1}{2} = \frac{3}{2}.</math>
 +
To calculate the second term, we need to use the identity <math>\sin^2 x + \cos^2 x = 1.</math> From the first and second equations, we can rewrite then as <math>\sin x = 3 \sin y</math> and <math>\cos x = \frac{1}{2} \cos y</math> respectively. Now, we can use the identity and make the equation <math>9 \sin^2 y + \frac{1}{4} \cos^2 y = 1</math> We now multiply both sides by 4 and get the equation <math>36 \sin^2 y + \cos^2 y = 4.</math> Using the identity again, we realize that we can subtract 1 from both sides and obtain <math>35 \sin^2 y = 3</math>. Now, we can figure out that <math>\sin^2 y = \frac{3}{35}</math>. Another identity that is useful for this problem is <math>\cos 2x = 1 - 2 \sin^2 x</math>. Now, we can find the value of <math>\cos 2y</math>
 +
 
 +
which is <math>1 - 2(\frac{3}{35}) = \frac{29}{35}</math>. Our main problem now is finding <math>\cos 2x</math>. We can use the identity so that we just need to find <math>\sin^2 x</math>. Using our first equation stated in the problem, we can multiply both sides by itself and get the equation <math>\frac{\sin^2 x}{\sin^2 y} = 9</math>. Plug in <math>\frac{3}{35}</math> for <math>\sin^2 y</math> and solve the equation to get the value of <math>\sin^2 x</math> as <math>\frac{27}{35}</math>. Next, we use the identity and find <math>\cos 2x</math> as <math>-\frac{19}{35}</math>. We can find the second term as we have <math>\cos 2x</math> and <math>\cos 2y</math>. Thus, the total sum is <math>\frac{3}{2} + \frac{-19}{29} = \frac{49}{58}</math>. The question asks the sum of the numerator and the denominator so the answer is <math>49 + 58 = \boxed{107}</math>.
  
 
== See Also ==
 
== See Also ==

Revision as of 01:46, 20 September 2025

Problem 9

Let $x$ and $y$ be real numbers such that $\frac{\sin x}{\sin y} = 3$ and $\frac{\cos x}{\cos y} = \frac12$. The value of $\frac{\sin 2x}{\sin 2y} + \frac{\cos 2x}{\cos 2y}$ can be expressed in the form $\frac pq$, where $p$ and $q$ are relatively prime positive integers. Find $p+q$.


Solution

Examine the first term in the expression we want to evaluate, $\frac{\sin 2x}{\sin 2y}$, separately from the second term, $\frac{\cos 2x}{\cos 2y}$.

The First Term

Using the identity $\sin 2\theta = 2\sin\theta\cos\theta$, we have:

$\frac{2\sin x \cos x}{2\sin y \cos y} = \frac{\sin x \cos x}{\sin y \cos y} = \frac{\sin x}{\sin y}\cdot\frac{\cos x}{\cos y}=3\cdot\frac{1}{2} = \frac{3}{2}$

The Second Term

Let the equation $\frac{\sin x}{\sin y} = 3$ be equation 1, and let the equation $\frac{\cos x}{\cos y} = \frac12$ be equation 2. Hungry for the widely-used identity $\sin^2\theta + \cos^2\theta = 1$, we cross multiply equation 1 by $\sin y$ and multiply equation 2 by $\cos y$.

Equation 1 then becomes:

$\sin x = 3\sin y$.

Equation 2 then becomes:

$\cos x = \frac{1}{2} \cos y$

Aha! We can square both of the resulting equations and match up the resulting LHS with the resulting RHS:

$1 = 9\sin^2 y + \frac{1}{4} \cos^2 y$

Applying the identity $\cos^2 y = 1 - \sin^2 y$ (which is similar to $\sin^2\theta + \cos^2\theta = 1$ but a bit different), we can change $1 = 9\sin^2 y + \frac{1}{4} \cos^2 y$ into:

$1 = 9\sin^2 y + \frac{1}{4} - \frac{1}{4} \sin^2 y$

Rearranging, we get $\frac{3}{4} = \frac{35}{4} \sin^2 y$.

So, $\sin^2 y = \frac{3}{35}$.

Squaring Equation 1 (leading to $\sin^2 x = 9\sin^2 y$), we can solve for $\sin^2 x$:

$\sin^2 x = 9\left(\frac{3}{35}\right) = \frac{27}{35}$

Using the identity $\cos 2\theta = 1 - 2\sin^2\theta$, we can solve for $\frac{\cos 2x}{\cos 2y}$.

$\cos 2x = 1 - 2\sin^2 x = 1 - 2\cdot\frac{27}{35} = 1 - \frac{54}{35} = -\frac{19}{35}$

$\cos 2y = 1 - 2\sin^2 y = 1 - 2\cdot\frac{3}{35} = 1 - \frac{6}{35} = \frac{29}{35}$

Thus, $\frac{\cos 2x}{\cos 2y} = \frac{-19/35}{29/35} = -\frac{19}{29}$.

Plugging in the numbers we got back into the original equation :

We get $\frac{\sin 2x}{\sin 2y} + \frac{\cos 2x}{\cos 2y} = \frac32 + \left(-\frac{19}{29} \right) = \frac{49}{58}$.

So, the answer is $49+58=\boxed{107}$.

Solution 2

As mentioned above, the first term is clearly $\frac{3}{2}.$ For the second term, we first wish to find $\frac{\cos 2x}{\cos 2y} =\frac{2\cos^2 x - 1}{2 \cos^2y -1}.$ Now we first square the first equation getting $\frac{\sin^2x}{\sin^2y} =\frac{1-\cos^2x}{1 - \cos^2y} =9.$ Squaring the second equation yields $\frac{\cos^2x}{\cos^2y} =\frac{1}{4}.$ Let $\cos^2x = a$ and $\cos^2y = b.$ We have the system of equations \begin{align*} 1-a &= 9-9b \\ 4a &= b \\ \end{align*} Multiplying the first equation by $4$ yields $4-4a = 36 - 36b$ and so $4-b =36 - 36b \implies b =\frac{32}{35}.$ We then find $a =\frac{8}{35}.$ Therefore the second fraction ends up being $\frac{\frac{64}{35}-1}{\frac{16}{35}-1} = -\frac{19}{29}$ so that means our desired sum is $\frac{49}{58}$ so the desired sum is $\boxed{107}.$

Solution 3

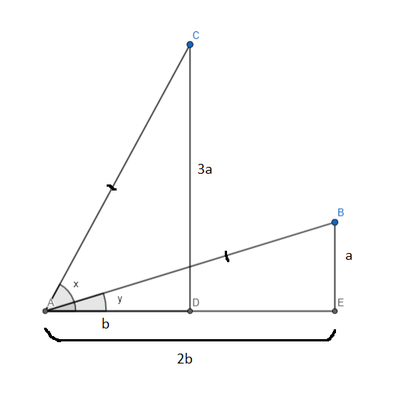
Dgxje.png

We draw 2 right triangles with angles x and y that have the same hypotenuse.

We get $b^2 + 9a^2 = 4b^2 + a^2$. Then, we find $8a^2 = 3b^2$.

Now, we can scale the triangle such that $a = \sqrt{3}$, $b = \sqrt{8}$. We find all the side lengths, and we find the hypotenuse of both these triangles to equal $\sqrt{35}$ This allows us to find sin and cos easily.

The first term is $\frac{3}{2}$, refer to solution 1 for how to find it.

The second term is $\frac{\cos^2(x) - \sin^2(x)}{\cos^2(y) - \sin^2(y)}$. Using the diagram, we can easily compute this as $\frac{\frac{8}{35} - \frac{27}{35}}{\frac{32}{35} - \frac{3}{35}} = \frac{-19}{29}$

Summing these you get $\frac{3}{2} + \frac{-19}{29} = \frac{49}{58} \implies \boxed{107}$

-Alexlikemath

Solution 4

Let $a = \sin(x), b = \sin(y)$ The first equation yields $\frac{a}{b} = 3.$ Using $sin^2(x) + cos^2(x) = 1$ the second equation yields \[\frac{\sqrt{1-a^2}}{\sqrt{1-b^2}} = \frac{1}{2} \rightarrow \frac{1-a^2}{1-b^2} = \frac{1}{4}\]

Solving this yields $\left(a, b\right) = \left(3\sqrt{\frac{3}{35}},\sqrt{\frac{3}{35}}\right).$ Finding the first via double angle for sin yields \[\frac{\sin(2x)}{\sin(2y)} = \frac{2\sin{x}\cos{x}}{2\sin{y}\cos{y}} = 3 \cdot \frac{1}{2} = \frac{3}{2}\] Double angle for cosine is \[\cos(2x) = 1-2\sin^2{x}\] so $\frac{\cos(2x)}{\sin(2x)} = \frac{1-2a^2}{1-2b^2} = -\frac{19}{29}.$ Adding yields $\frac{49}{58} \rightarrow 49 + 58 = \boxed{107}$

Solution 5

We can calculate the first term $\frac{\sin 2x}{\sin 2y} = \frac{2 \sin x \cos x}{2 \sin y \cos y} = 3 \cdot \frac{1}{2} = \frac{3}{2}.$ To calculate the second term, we need to use the identity $\sin^2 x + \cos^2 x = 1.$ From the first and second equations, we can rewrite then as $\sin x = 3 \sin y$ and $\cos x = \frac{1}{2} \cos y$ respectively. Now, we can use the identity and make the equation $9 \sin^2 y + \frac{1}{4} \cos^2 y = 1$ We now multiply both sides by 4 and get the equation $36 \sin^2 y + \cos^2 y = 4.$ Using the identity again, we realize that we can subtract 1 from both sides and obtain $35 \sin^2 y = 3$. Now, we can figure out that $\sin^2 y = \frac{3}{35}$. Another identity that is useful for this problem is $\cos 2x = 1 - 2 \sin^2 x$. Now, we can find the value of $\cos 2y$

which is $1 - 2(\frac{3}{35}) = \frac{29}{35}$. Our main problem now is finding $\cos 2x$. We can use the identity so that we just need to find $\sin^2 x$. Using our first equation stated in the problem, we can multiply both sides by itself and get the equation $\frac{\sin^2 x}{\sin^2 y} = 9$. Plug in $\frac{3}{35}$ for $\sin^2 y$ and solve the equation to get the value of $\sin^2 x$ as $\frac{27}{35}$. Next, we use the identity and find $\cos 2x$ as $-\frac{19}{35}$. We can find the second term as we have $\cos 2x$ and $\cos 2y$. Thus, the total sum is $\frac{3}{2} + \frac{-19}{29} = \frac{49}{58}$. The question asks the sum of the numerator and the denominator so the answer is $49 + 58 = \boxed{107}$.

See Also

2012 AIME II (Problems • Answer Key • Resources)
Preceded by
Problem 8 		Followed by
Problem 10
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. AMC Logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2012_AIME_II_Problems/Problem_9&oldid=260926"