Difference between revisions of "2018 AIME I Problems/Problem 8"
m (→Solution 2) |
(→Solution 1) |
||
| Line 8: | Line 8: | ||
-expiLnCalc | -expiLnCalc | ||
| + | |||
| + | ==Solution 2== | ||
| + | |||
| + | Like solution 1, draw out the large equilateral triangle with side length <math>24</math>. | ||
==See Also== | ==See Also== | ||
{{AIME box|year=2018|n=I|num-b=7|num-a=9}} | {{AIME box|year=2018|n=I|num-b=7|num-a=9}} | ||
{{MAA Notice}} | {{MAA Notice}} | ||
Revision as of 05:43, 8 March 2018
Let 
be an equiangular hexagon such that 
, and 
. Denote 
the diameter of the largest circle that fits inside the hexagon. Find 
.
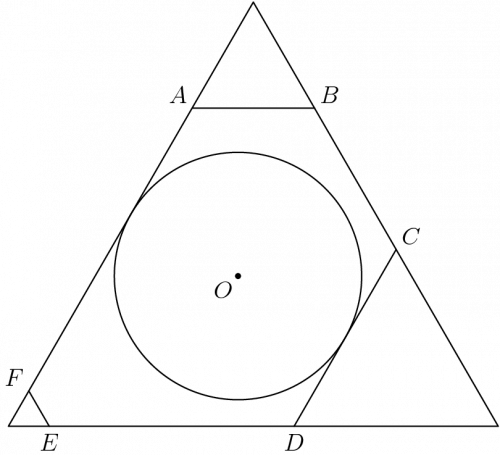
Solution 1
- cooljoseph
First of all, draw a good diagram! This is always the key to solving any geometry problem. Once you draw it, realize that 
. Why? Because since the hexagon is equiangular, we can put an equilateral triangle around it, with side length 
. Then, if you drew it to scale, notice that the "widest" this circle can be according to 
is 
. And it will be obvious that the sides won't be inside the circle, so our answer is 
.
-expiLnCalc
Solution 2
Like solution 1, draw out the large equilateral triangle with side length 
.
See Also
| 2018 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 7 |
Followed by Problem 9 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. 
