1972 IMO Problems/Problem 2
Contents
Problem
Prove that if ![]() , every quadrilateral that can be inscribed in a circle can be dissected into
, every quadrilateral that can be inscribed in a circle can be dissected into ![]() quadrilaterals each of which is inscribable in a circle.
quadrilaterals each of which is inscribable in a circle.
Solution
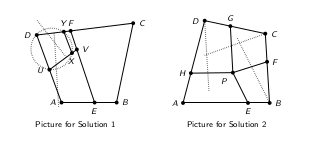
Our initial quadrilateral will be ![]() .
.
For ![]() , we do this:
, we do this:
Take ![]() with
with ![]() sufficiently close to
sufficiently close to ![]() respectively. Take
respectively. Take ![]() such that
such that ![]() is an isosceles trapezoid, with
is an isosceles trapezoid, with ![]() close enough to
close enough to ![]() (or
(or ![]() close enough to
close enough to ![]() ) that we can find a circle passing through
) that we can find a circle passing through ![]() (or
(or ![]() ) which cuts the segments
) which cuts the segments ![]() in
in ![]() . Our four cyclic quadrilaterals are
. Our four cyclic quadrilaterals are ![]() .
.
For ![]() we do the exact same thing as above, but now, since we have an isosceles trapezoid, we can add as many trapezoids as we want by dissecting the one trapezoid with lines parallel to its bases.
we do the exact same thing as above, but now, since we have an isosceles trapezoid, we can add as many trapezoids as we want by dissecting the one trapezoid with lines parallel to its bases.
The above solution was posted and copyrighted by grobber. The original thread for this problem can be found here: [1]
Remarks (added by pf02, March 2025)
The construction described in the solution above is correct (in the sense that it describes a legitimate way of dissecting an inscribable quadrilateral into four inscribable quadrilaterals). However, the solution is incomplete and sloppily written.
Below I will discuss and complete the solution given above.
Then, I will give a second solution. And finally, I will
discuss the cases when ![]() .
.
Discussion and completion of the above solution
The first issue is the fact that a construction is described, but there is no proof, not even a hint, why the the quadrilaterals are inscribable. This is not obvious, and it needs a proof. I will give the proof below.
The second issue is the vagueness of "close enough" used twice
in the proof. The first time it is used, "![]() sufficiently
close to
sufficiently
close to ![]() respectively" is not needed (indeed, and segment
respectively" is not needed (indeed, and segment
![]() parallel to
parallel to ![]() would do), so there is no need to make
this more precise. The second time it is used, namely "
would do), so there is no need to make
this more precise. The second time it is used, namely "![]() close enough to
close enough to ![]() (or
(or ![]() close enough to
close enough to ![]() ) that we can
find a circle passing through
) that we can
find a circle passing through ![]() (or
(or ![]() )" is indeed
needed, and it is not at all clear what "close enough" should
be, or that this is at all possible. I will come back to this
shortly.
)" is indeed
needed, and it is not at all clear what "close enough" should
be, or that this is at all possible. I will come back to this
shortly.
The third issue is poor wording. We don't need to "add as many trapezoids as we want". We want to dissect the one isosceles trapezoid into as many isosceles trapezoids as we want by lines parallel to its bases.
Before giving the missing details, let us remember that a quadrilateral
![]() is inscribable if and only if a pair of opposing angles adds
up to
is inscribable if and only if a pair of opposing angles adds
up to ![]() , in other words
, in other words ![]() , or equivalently,
, or equivalently,
![]() . In particular, any isosceles trapezoid is
inscribable.
. In particular, any isosceles trapezoid is
inscribable.
Now let us show that the four quadrilaterals are inscribable. It is easy
to see that the first one, ![]() is inscribable. Indeed,
is inscribable. Indeed,
![]() . We know that
. We know that ![]() because
of parallelism, so
because
of parallelism, so ![]() . The second one,
. The second one, ![]() is an isosceles trapezoid by the choice of
is an isosceles trapezoid by the choice of ![]() , so it is inscribable.
The third one,
, so it is inscribable.
The third one, ![]() is inscribable by construction. It remains to be
shown that
is inscribable by construction. It remains to be
shown that ![]() is inscribable.
is inscribable.
We have ![]() . This shows that
. This shows that ![]() is inscribable.
is inscribable.
Note that as suggested by the solution, we could have chosen ![]() so
that
so
that ![]() is inscribable, in which case a similar argument would have
shown that
is inscribable, in which case a similar argument would have
shown that ![]() is inscribable as well.
is inscribable as well.
Let us now make precise what it means that ![]() should be close enough to
should be close enough to ![]() ,
or
,
or ![]() should be close enough to
should be close enough to ![]() , so that we can find
, so that we can find ![]() .
.
TO BE CONTINUED. SAVING MID WAY, SO I DON'T LOOSE WORK DONE SO FAR.
See Also
| 1972 IMO (Problems) • Resources | ||
| Preceded by Problem 1 |
1 • 2 • 3 • 4 • 5 • 6 | Followed by Problem 3 |
| All IMO Problems and Solutions | ||