Introduction

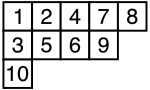
The hook length theorem is a theorem to be used on Standard Young Tableau. A standard Young Tableau is essentially a pack of blocks together, such as this one:

A tableau has a decreasing(not strictly decreasing) number of blocks in every row.

A Standard Young Tableau(SYT) has increasing numbers in both rows and columns. As shown in the figure, 1-3-10 is increasing, as well as 2-5, 4-6, 7-9, 1-2-4-7-8, and 3-5-6-9.

Theorem

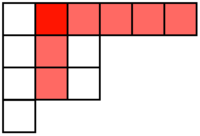
Let the number of cells in a Young tableau be n. Define a hook length of a block to be the number of blocks to the right and below the block, including the block. In the below image, the hook of the red square is $7$ .

Let the product of all the hook lengths be $h$ . Then the number of possible standard Young tableaux is $\frac{n!}{h}$ .

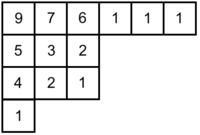
The number of hooks of each block in the example tableau is shown below.

So in the example, the number of SYTs is $\frac{13!}{9\times7\times6\times3\times2\times1\times5\times3\times2\times4\times2\times1\times1} = 11440$ .

Problem

2016 USAMO P2

Page

Toolbox

Search

Hook Length Theorem

Introduction

Theorem

Problem