2024 AMC 12B Problems/Problem 21

1 Problem
2 Solution 1
3 Solution 2 (Complex Number)
4 Solution 3 (Another Trig)
- 4.1 Solution 3.1 (Different Flavor of the same thing)
5 Solution 4 (Similarity)
6 Solution 5 (Complex)
7 Solution 6 (Law of Cosines)
- 7.1 Solution 6.1 (Faster Ending)
8 Solution 7 (No Trig, Coord Bash)
9 Solution 8 (Linear Algebra)
10 Video Solution by Innovative Minds
11 Video Solution by SpreadTheMathLove
12 See also

Problem

The measures of the smallest angles of three different right triangles sum to $90^\circ$ . All three triangles have side lengths that are primitive Pythagorean triples. Two of them are $3-4-5$ and $5-12-13$ . What is the perimeter of the third triangle?

$\textbf{(A) } 40 \qquad\textbf{(B) } 126 \qquad\textbf{(C) } 154 \qquad\textbf{(D) } 176 \qquad\textbf{(E) } 208$

Solution 1

Let $\alpha$ and $\beta$ be the smallest angles of the $3-4-5$ and $5-12-13$ triangles respectively. We have $\tan(\alpha)=\frac{3}{4} \text{ and } \tan(\beta)=\frac{5}{12}$ Then $\tan(\alpha+\beta)=\frac{\frac{3}{4}+\frac{5}{12}}{1-\frac{3}{4}\cdot\frac{5}{12}}=\frac{56}{33}$ Let $\theta$ be the smallest angle of the third triangle. Consider $\tan{90^\circ}=\tan((\alpha+\beta)+\theta)=\frac{\frac{56}{33}+\tan{\theta}}{1-\frac{56}{33}\cdot\tan{\theta}}$ In order for this to be undefined, we need $1-\frac{56}{33}\cdot\tan{\theta}=0$ so $\tan{\theta}=\frac{33}{56}$ Hence the base side lengths of the third triangle are $33$ and $56$ . By the Pythagorean Theorem, the hypotenuse of the third triangle is $65$ , so the perimeter is $33+56+65=\boxed{\textbf{(C) }154}$ .

~kafuu_chino

Solution 2 (Complex Number)

The smallest angle of $3-4-5$ triangle can be viewed as the arguement of $4+3i$ , and the smallest angle of $5-12-13$ triangle can be viewed as the arguement of $12+5i$ .

Hence, if we assume the ratio of the two shortest length of the last triangle is $1:k$ ( $k$ being some rational number), then we can derive the following formula of the sum of their arguement. Since their arguement adds up to $\frac{\pi}{2}$ , it's the arguement of $i$ . Hence, $\left(4+3i\right)\left(12+5i\right)\left(k+i\right)=ni\,,$ where $n$ is some real number.

Solving the equation, we get $56k-33=0\,,\quad 33k+56=n\,.$ Hence $k=\frac{33}{56}$

Since the sidelength of the theird triangle are co-prime integers, two of its sides are $33$ and $56$ . And the last side is $\sqrt{33^2+56^2}=65$ , hence, the parameter of the third triangle if $33+56+65=\boxed{\mathbf{(C)}\,154}$ .

~Prof. Joker

Solution 3 (Another Trig)

Denote the smallest angle of the $3-4-5$ triangle as $\alpha$ , the smallest angle of the $5-12-13$ triangle as $\beta$ , and the smallest angle of the triangle we are trying to solve for as $\theta$ . We then have $\alpha + \beta + \theta = 90$ $\alpha + \beta = 90 - \theta$ $\sin{(\alpha + \beta)} = \sin{(90 - \theta)} = \cos{\theta}$ $\cos{\theta} = \sin{\alpha}\cos{\beta} + \cos{\alpha}\sin{\beta} = (\frac{3}{5})(\frac{12}{13}) + (\frac{4}{5})(\frac{5}{13}) = \frac{56}{65}$ Taking the hypotenuse to be $65$ and one of the legs to be $56$ , we compute the last leg to be $\sqrt{65^2 - 56^2} = \sqrt{(65-56)(65+56)} = \sqrt{9*121} = 3*11 = 33$

Giving us a final answer of $65 + 56 + 33 = \boxed{\textbf{(C) }154}$ .

~tkl

Solution 3.1 (Different Flavor of the same thing)

Consider $\sin(\theta) = \sin(90 - (\alpha + \beta)) = \cos(\alpha + \beta) = \frac{33}{65}$ using the cosine addition identity. Instead of using the Pythagorean theorem, we can use Euclid's formula since we're dealing with primitive triples.

$65 = a^2 + b^2$ $33 = a^2 - b^2$

Combining that, we get $a = 7$ and $b=4$ . Using this, we can get that the other leg must be $2ab = 56$ . We add the lengths and get that the perimeter is $56 + 65 + 33 = \boxed{154}$ .

~ sxbuto

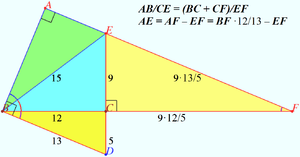
Solution 4 (Similarity)

Let's arrange the triangles $BCD (5-12-13), BCE (9-12-15)$ and $ABE$ as shown in the diagram. $F = AE \cap BC.$ $AE \perp AB, DB \perp AB \implies \triangle BCD \sim \triangle FCE \sim \triangle FAB \implies$ $EF = \frac{9 \cdot 13}{5}, CF = \frac{9 \cdot 12}{5}, BF = BC + CF = \frac{12 \cdot 14}{5},$ $\frac {AB}{CE} = \frac {BF}{EF} \implies AB = \frac{12 \cdot 14}{13},$ $AE = AF - EF = BF \cdot \frac {12}{13} - EF = \frac {99}{13} \implies$ $AE : AB : BE = 99 : 12 \cdot 14 : 15 \cdot 13 = 33 : 56 : 65 \implies 65 + 56 + 33 = \boxed{\textbf{(C) }154}$ vladimir.shelomovskii@gmail.com, vvsss

Solution 5 (Complex)

Suppose the triangle has legs $a, b$ . We want $\arctan \frac{3}{4} + \arctan\frac{5}{12} + \arctan\frac{a}{b} = \frac{\pi}{2}.$ This is equivalent to $\begin{align*} \arg{e^{i\arctan\frac{3}{4}}\cdot e^{i\arctan\frac{5}{12}}\cdot e^{i\arctan\frac{a}{b}}} &= \frac{\pi}{2}\\ \arg(4+3i)(12+5i)(b+ai) &= \frac{\pi}{2}\\ \arg\left( (33b -56a)+(33a + 56b)i\right) &= \frac{\pi}{2} \end{align*}$ Since the argument of this complex number is $\frac{\pi}{2},$ its real part must be $0$ . Matching real and imaginary parts yields $33b = 56a,$ or $b = \frac{56}{33}a$ . The smallest pair $(a, b)$ that works is $(33, 56),$ which yields a hypotenuse of $65.$ The perimeter of this triangle is $33 + 56 + 65 = \boxed{\textbf{(C)\ 154}}.$

-Benedict T (countmath1)

Solution 6 (Law of Cosines)

We can start by scaling the $3-4-5$ right triangle up by a factor of $3$ and "gluing" it to the $5-12-13$ triangle's longer leg. Let $\alpha$ , $\beta$ , and $\theta$ be the smallest angles in the $3-4-5$ , $5-12-13$ and unknown triangle respectively. We can construct the following diagram of the two known triangles. $[asy] pair A = (0,0); pair B = (5,0); pair C = (14,0); pair D = (5,12); draw(A--C--D--cycle); draw(B--D); draw(rightanglemark(A,B,D,20)); label("5", A--B, S); label("9", B--C, S); label("15", C--D, NE); label("13", D--A, NW); label("12", B--D, E); label("$\beta$", D, 6*dir(257)); label("$\alpha$", D, 4*dir(287)); [/asy]$

We can also construct a diagram for the third, unknown triangle like so. We know that $\alpha+\beta+\theta=90$ , and therefore that $\theta=90-\alpha-\beta$ . We also know that the other acute angle in this third triangle will have a measure of $\alpha+\beta$ by the triangle angle sum theorem. $[asy] pair A = (0,0); pair B = (56,0); pair C = (56,33); draw(A--B--C--cycle); draw(rightanglemark(A,B,C,50)); label("$90-\alpha-\beta$", A, 8*dir(12)); label("$\alpha+\beta$", C, 6*dir(242)); [/asy]$ We can use the law of cosines on the triangle in the first diagram to get the equation $14^2=15^2+13^2-2(13)(15)\cos{(\alpha+\beta)}$ . Isolating $\cos{(\alpha+\beta)}$ , we get $-198=-390\cos{(\alpha+\beta)}$ , which further simplifies to $\cos{(\alpha+\beta)}=\frac{198}{390}$ . Since the third triangle has to be a primitive Pythagorean triple, we must take this trig ratio into its most simple form, namely $\cos{(\alpha+\beta)}=\frac{33}{65}$ . Using this information in our second diagram, we know that the smaller, adjacent leg must have length $33$ , and the hypotenuse must have length $65$ . We can then use the Pythagorean theorem to find the other, unknown leg, which has length $56$ . Adding these three lengths together, we find that the perimeter of this right triangle is $33+56+65=\boxed{\textbf{(C)\ 154}}$ .

~Phinetium

Solution 6.1 (Faster Ending)

Instead of computing $\sqrt{65^2-33^2}$ to find the second leg in the unknown triangle by hand, we can use process of elimination. $\textbf{(B)}\ 126$ and $\textbf{(C)}\ 154$ are the only answers within the realm of possibility, because $\textbf{(A)}\ 40$ would entitle a triangle with a negative side length, and $\textbf{(D)}\ 176$ and $\textbf{(E)}\ 208$ would require legs greater than the length of the hypotenuse. The answer choice $\textbf{(B)}\ 126$ would force the second leg to have a length of $28$ , which is smaller than the smallest leg in the triangle. (We know that the leg with length $33$ is the smallest leg in the triangle by the side-angle relationship theorem, because it is opposite the smallest angle in the triangle.) Therefore, the only valid answer choice remaining is $\boxed{\textbf{(C)\ 154}}$ .

~Phinetium (again)

Solution 7 (No Trig, Coord Bash)

Set up a coordinate system. Let $(0, 0)$ , $(4, 0)$ , and $(0, 3)$ be the vertices of the base $3-4-5$ right triangle. In this case, the three smallest angles will all be at $(4, 0)$ , and one of the coordinates of the unknown triangle has to lie on the line $x = 4$ . Now, scale down the $5-12-13$ triangle by $\frac{5}{12}$ so that the new sides are $\frac{25}{12}-5-\frac{65}{12}$ , and place the side with length 5 at the coordinates $(0, 3)$ and $(4, 0)$ . The line passing through these two points can be written as $y = -\frac{3}{4}x + 3$ , so the perpendicular of this line at $(0, 3)$ can be written as $y = \frac{4}{3}x + 3$ . Since the length of the other side is $\frac{25}{12}$ , after drawing smaller $3-4-5$ right triangles, we find that the third coordinate of the $\frac{25}{12}-5-\frac{65}{12}$ is at $(\frac{5}{4}, \frac{14}{3})$ . This coordinate will be one of the coordinates for our unknown triangle. We can place the other coordinate of the unknown triangle at $(4, \frac{14}{3})$ and the third is, by definition, at $(4, 0)$ . The distance from $(\frac{5}{4}, \frac{14}{3})$ to $(4, \frac{14}{3})$ is $\frac{11}{4}$ , and the distance from $(4, \frac{14}{3})$ to $(4, 0)$ is $\frac{14}{3}$ , and from before, the distance from $(\frac{5}{4}, \frac{14}{3})$ to $(4, 0)$ is $\frac{65}{12}$ . Scaling up the sides so that they are integers, we see that the side lengths make a $33-56-65$ right triangle. The perimeter is then $33+56+65=\boxed{\textbf{(C)\ 154}}$ .

~mathwizard123123

Solution 8 (Linear Algebra)

Because the three smallest angles add up to $90^\circ$ , you can imagine putting the $3-4-5$ and $5-12-13$ triangles on the $y$ -axis and $x$ -axis, respectively, in the first quadrant. So that all 3 triangles will have their smallest angle meet at the origin and exactly fill up the first quadrant.

Now the $3-4-5$ and $5-12-13$ triangles describe the vectors $\langle 3, 4 \rangle$ and $\langle 12, 5 \rangle$ with the smallest angle of the third triangle, $\theta$ , between them. We can find $cos(\theta)$ by taking the dot product and dividing by the magnitudes of the vectors (which are the hypotenuses that we know to be 5 and 13).

$\begin{align*} \cos \theta = \frac{\langle 3, 4 \rangle \cdot \langle 12, 5 \rangle}{\|\langle 3, 4 \rangle\| \, \|\langle 12, 5 \rangle\|} = \frac{3 \cdot 12 + 4 \cdot 5}{5 \cdot 13} = \frac{56}{65} \end{align*}$

This ratio $\cos \theta = \frac{56}{65}$ describes the third triangle to have a hypotenuse with length $65$ , one leg with length $56$ , and another leg with length $\sqrt{65^2 - 56^2} = \sqrt{(65 - 56)(65 + 56)} = \sqrt{9 \cdot 121} = 33$ by Pythagorean and difference of squares.

The perimeter is then $65 + 56 + 33 = \boxed{\textbf{(C)\ 154}}$

~CorpulentAxolotl

Video Solution by Innovative Minds

https://youtu.be/9PMdtwkKTlU

Video Solution by SpreadTheMathLove

https://www.youtube.com/watch?v=cyiF8_5fEsM

2024 AMC 12B (Problems • Answer Key • Resources)
Preceded by Problem 20	Followed by Problem 22
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

Page

Toolbox

Search