1983 AHSME Problems/Problem 17
Problem
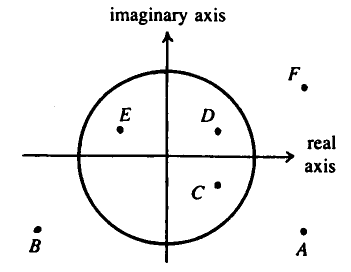
The diagram above shows several numbers in the complex plane. The circle is the unit circle centered at the origin.
One of these numbers is the reciprocal of 
. Which one?
Solution 1 (Linear Modeling)
The reciprocal of a number \( a \) is \( \frac{1}{a} \).
We start with \( F \) and the point \( (1, 0i) \) where \( i = \sqrt{-1} \). Draw a line through these two points.
The reciprocal of a line is legitimately a vertical shrink or a horizontal stretch (the line gets farther away from the \( i_1 \) axis but closer to the real axis). Therefore the line must pass through point 
as it is the only point that is closest to the real axis whilst maintaining a reflection over the imaginary axis.
~Pinotation
Solution 2
Write as 
, where we see from the diagram that 
and 
(as is outside the unit circle). We have 
, so, since , the reciprocal of has a positive real part and negative imaginary part. Also, the reciprocal has magnitude equal to the reciprocal of 's magnitude (since 
); as 's magnitude is greater than 
, its reciprocal's magnitude will thus be between 
and , so its reciprocal will be inside the unit circle. Therefore, the only point shown which could be the reciprocal of is point .
Solution 3 (Polar Form)
Let 
be the complex number at in polar form. Then 
. Since is outside the circle, 
, and therefore 
. So 
must be inside the circle and on the line which is 
clockwise from the real axis, that is 
.
-j314andrews
See Also
| 1983 AHSME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 16 |
Followed by Problem 18 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 • 26 • 27 • 28 • 29 • 30 | ||
| All AHSME Problems and Solutions | ||
These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. 
