2022 AIME II Problems/Problem 15
Contents
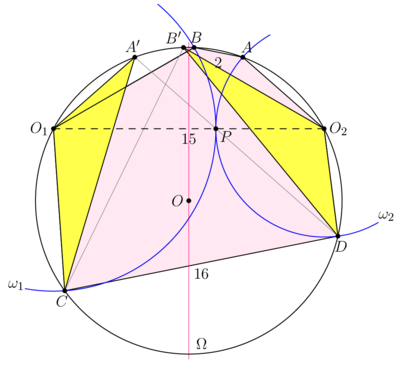
Problem
Two externally tangent circles ![]() and
and ![]() have centers
have centers ![]() and
and ![]() , respectively. A third circle
, respectively. A third circle ![]() passing through
passing through ![]() and
and ![]() intersects
intersects ![]() at
at ![]() and
and ![]() and
and ![]() at
at ![]() and
and ![]() , as shown. Suppose that
, as shown. Suppose that ![]() ,
, ![]() ,
, ![]() , and
, and ![]() is a convex hexagon. Find the area of this hexagon.
is a convex hexagon. Find the area of this hexagon.
![[asy] import geometry; size(10cm); point O1=(0,0),O2=(15,0),B=9*dir(30); circle w1=circle(O1,9),w2=circle(O2,6),o=circle(O1,O2,B); point A=intersectionpoints(o,w2)[1],D=intersectionpoints(o,w2)[0],C=intersectionpoints(o,w1)[0]; filldraw(A--B--O1--C--D--O2--cycle,0.2*fuchsia+white,black); draw(w1); draw(w2); draw(O1--O2,dashed); draw(o); dot(O1); dot(O2); dot(A); dot(D); dot(C); dot(B); label("$\omega_1$",8*dir(110),SW); label("$\omega_2$",5*dir(70)+(15,0),SE); label("$O_1$",O1,W); label("$O_2$",O2,E); label("$B$",B,N+1/2*E); label("$A$",A,N+1/2*W); label("$C$",C,S+1/4*W); label("$D$",D,S+1/4*E); label("$15$",midpoint(O1--O2),N); label("$16$",midpoint(C--D),N); label("$2$",midpoint(A--B),S); label("$\Omega$",o.C+(o.r-1)*dir(270)); [/asy]](http://latex.artofproblemsolving.com/7/b/9/7b94456c42eaed4f905c8c8fbc0555d154676d57.png)
Solution 1
First observe that ![]() and
and ![]() . Let points
. Let points ![]() and
and ![]() be the reflections of
be the reflections of ![]() and
and ![]() , respectively, about the perpendicular bisector of
, respectively, about the perpendicular bisector of ![]() . Then quadrilaterals
. Then quadrilaterals ![]() and
and ![]() are congruent, so hexagons
are congruent, so hexagons ![]() and
and ![]() have the same area. Furthermore, triangles
have the same area. Furthermore, triangles ![]() and
and ![]() are congruent, so
are congruent, so ![]() and quadrilateral
and quadrilateral ![]() is an isosceles trapezoid.
is an isosceles trapezoid.
![[asy] import olympiad; size(180); defaultpen(linewidth(0.7)); pair Ap = dir(105), Bp = dir(75), O1 = dir(25), C = dir(320), D = dir(220), O2 = dir(175); draw(unitcircle^^Ap--Bp--O1--C--D--O2--cycle); label("$A'$",Ap,dir(origin--Ap)); label("$B'$",Bp,dir(origin--Bp)); label("$O_1$",O1,dir(origin--O1)); label("$C$",C,dir(origin--C)); label("$D$",D,dir(origin--D)); label("$O_2$",O2,dir(origin--O2)); draw(O2--O1,linetype("4 4")); draw(Ap--D^^Bp--C,linetype("2 2")); [/asy]](http://latex.artofproblemsolving.com/8/a/4/8a4698486f5397ef610a64ee840efec7ff7e7c21.png) Next, remark that
Next, remark that ![]() , so quadrilateral
, so quadrilateral ![]() is also an isosceles trapezoid; in turn,
is also an isosceles trapezoid; in turn, ![]() , and similarly
, and similarly ![]() . Thus, Ptolemy's theorem on
. Thus, Ptolemy's theorem on ![]() yields
yields ![]() , whence
, whence ![]() . Let
. Let ![]() . The Law of Cosines on triangle
. The Law of Cosines on triangle ![]() yields
yields
![]() and hence
and hence ![]() . Thus the distance between bases
. Thus the distance between bases ![]() and
and ![]() is
is ![]() (in fact,
(in fact, ![]() is a
is a ![]() triangle with a
triangle with a ![]() triangle removed), which implies the area of
triangle removed), which implies the area of ![]() is
is ![]() .
.
Now let ![]() and
and ![]() ; the tangency of circles
; the tangency of circles ![]() and
and ![]() implies
implies ![]() . Furthermore, angles
. Furthermore, angles ![]() and
and ![]() are opposite angles in cyclic quadrilateral
are opposite angles in cyclic quadrilateral ![]() , which implies the measure of angle
, which implies the measure of angle ![]() is
is ![]() . Therefore, the Law of Cosines applied to triangle
. Therefore, the Law of Cosines applied to triangle ![]() yields
yields

Thus ![]() , and so the area of triangle
, and so the area of triangle ![]() is
is ![]() .
.
Thus, the area of hexagon ![]() is
is ![]() .
.
~djmathman
Additional Graph for Better Understanding (Rearranging of the Pizza Slices)
This is how the reflection mentioned above is actually done. The reflection is actually a reorganization of the red and blue triangles, creating a symmetric figure with a isosceles trapezoid without changing the area. Basically you rearrange them so that each side contains a red triangle above a blue one. Then you calculate the area of the trapezoid and the two congruent triangles beside.
~cassphe
Solution 2
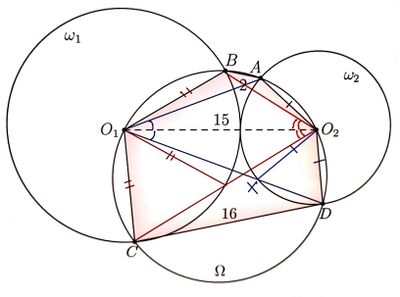
Denote by ![]() the center of
the center of ![]() .
Denote by
.
Denote by ![]() the radius of
the radius of ![]() .
.
We have ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() are all on circle
are all on circle ![]() .
.
Denote ![]() .
Denote
.
Denote ![]() .
Denote
.
Denote ![]() .
.
Because ![]() and
and ![]() are on circles
are on circles ![]() and
and ![]() ,
, ![]() is a perpendicular bisector of
is a perpendicular bisector of ![]() . Hence,
. Hence, ![]() .
.
Because ![]() and
and ![]() are on circles
are on circles ![]() and
and ![]() ,
, ![]() is a perpendicular bisector of
is a perpendicular bisector of ![]() . Hence,
. Hence, ![]() .
.
In ![]() ,
,
![]()
Hence,
![]()
In ![]() ,
,

Hence,
![]()
In ![]() ,
,

Hence,
![]()
Taking ![]() , we get
, we get ![]() .
Thus,
.
Thus, ![]() .
.
Taking these into (1), we get ![]() .
Hence,
.
Hence,

Hence, ![]() .
.
In ![]() ,
,
![]()
In ![]() , by applying the law of sines, we get
, by applying the law of sines, we get
![]()
Because circles ![]() and
and ![]() are externally tangent,
are externally tangent, ![]() is on circle
is on circle ![]() ,
, ![]() is on circle
is on circle ![]() ,
,

Thus, ![]() .
.
Now, we compute ![]() and
and ![]() .
.
Recall ![]() and
and ![]() .
Thus,
.
Thus, ![]() .
.
We also have

Thus,

Therefore,

~Steven Chen (www.professorchenedu.com)
Solution 3
Let points ![]() and
and ![]() be the reflections of
be the reflections of ![]() and
and ![]() respectively, about the perpendicular bisector of
respectively, about the perpendicular bisector of ![]()
![]()
![]() We establish the equality of the arcs and conclude that the corresponding chords are equal
We establish the equality of the arcs and conclude that the corresponding chords are equal
![]()
![]() Similarly
Similarly ![]()
Ptolemy's theorem on ![]() yields
yields ![]()
![]() The area of the trapezoid
The area of the trapezoid ![]() is equal to the area of an isosceles triangle with sides
is equal to the area of an isosceles triangle with sides
![]() and
and ![]()
The height of this triangle is ![]() The area of
The area of ![]() is
is ![]()
![]()
![]()
Denote ![]()
![]() hence
hence ![]()
![]()
Semiperimeter of ![]() is
is ![]()
The distance from the vertex ![]() to the tangent points of the inscribed circle of the triangle
to the tangent points of the inscribed circle of the triangle ![]() is equal
is equal ![]()
The radius of the inscribed circle is ![]()
The area of triangle ![]() is
is ![]()
The hexagon ![]() has the same area as hexagon
has the same area as hexagon ![]()
The area of hexagon ![]() is equal to the sum of the area of the trapezoid
is equal to the sum of the area of the trapezoid ![]() and the areas of two equal triangles
and the areas of two equal triangles ![]() and
and ![]() so the area of the hexagon
so the area of the hexagon ![]() is
is ![]()
vladimir.shelomovskii@gmail.com, vvsss
Solution 4
Let circle ![]() 's radius be
's radius be ![]() , then the radius of circle
, then the radius of circle ![]() is
is ![]() . Based on Brahmagupta's Formula,
. Based on Brahmagupta's Formula,
the hexagon's Area ![]() .
.
Now we only need to find the ![]() .
.
Connect ![]() and
and ![]() ,
, ![]() and
and ![]() , and let
, and let ![]() be the point of intersection between
be the point of intersection between ![]() and circle
and circle ![]() , based on the " 2 Non-Congruent Triangles of 'SSA' Scenario " , we can immediately see
, based on the " 2 Non-Congruent Triangles of 'SSA' Scenario " , we can immediately see ![]() and therefore get an equation from the "Power of A Point Theorem:
and therefore get an equation from the "Power of A Point Theorem:
![]() (1).
(1).
Similarly,
![]() (2).
(2).
We can also get two other equations about these 4 segments from Ptolemy's Theorem:
![]() (3)
(3)
![]() (4)
(4)
Multiply equations (1) and (2), and equations (3) and (4) respectively, we will get a very simple and nice equation of ![]() :
:
![]() ,
,
then:
![]() .
.
This result is good enough for us to find the hexagon's area, which:



.
eJMaSc
Solution 5 (Super bash)
![[asy] import geometry; size(10cm); point O1=(0,0),O2=(15,0),B=9*dir(30); circle w1=circle(O1,9),w2=circle(O2,6),o=circle(O1,O2,B); point A=intersectionpoints(o,w2)[1],D=intersectionpoints(o,w2)[0],C=intersectionpoints(o,w1)[0]; filldraw(A--B--O1--C--D--O2--cycle,0.2*fuchsia+white,black); draw(w1); draw(w2); draw(O1--O2,dashed); draw(o); dot(O1); dot(O2); dot(A); dot(D); dot(C); dot(B); label("$\omega_1$",8*dir(110),SW); label("$\omega_2$",5*dir(70)+(15,0),SE); label("$O_1$",O1,W); label("$O_2$",O2,E); label("$B$",B,N+1/2*E); label("$A$",A,N+1/2*W); label("$C$",C,S+1/4*W); label("$D$",D,S+1/4*E); label("$15$",midpoint(O1--O2),N); label("$16$",midpoint(C--D),N); label("$2$",midpoint(A--B),S); label("$x$", midpoint(O1--B),N); label("$x$", midpoint(O1--C),E); label("$15-x$", midpoint(O2--A),W); label("$15-x$", midpoint(O2--D),E); label("$\Omega$",o.C+(o.r-1)*dir(270)); [/asy]](http://latex.artofproblemsolving.com/1/9/f/19f4d8f9f823041ea038a39bd4ba80e569646271.png)
Start by noting that the radius of ![]() and
and ![]() sum up to 15.
sum up to 15.
Let the radius of ![]() be
be ![]() , then the radius of
, then the radius of ![]() will be
will be ![]() . We can find the area of the hexagon as the sum of the area of the quadrilateral
. We can find the area of the hexagon as the sum of the area of the quadrilateral ![]() and
and ![]() , which is given by the Brahmagupta's Formula as:
, which is given by the Brahmagupta's Formula as: ![]() , we only need
, we only need ![]() , and the condition is sufficient already. Note that the total number of diagonals and sides of the hexagon is
, and the condition is sufficient already. Note that the total number of diagonals and sides of the hexagon is ![]() , 2 pairs of them
, 2 pairs of them ![]() , and
, and ![]() can all be represented by the same variable
can all be represented by the same variable ![]() , and 3 of them (
, and 3 of them (![]() ) are given. Therefore, the total number of variables is
) are given. Therefore, the total number of variables is ![]() . And we have
. And we have ![]() equations by doing ptolemy on the quadrilaterals inside the hexagon, we can list some of them out in hope of bashing for a solution:
equations by doing ptolemy on the quadrilaterals inside the hexagon, we can list some of them out in hope of bashing for a solution:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
15 equations, 9 variables, hopefully one can solve this.
The question is especially disgusting in the sense that there is not a lot of geometric properties or hypothesis that one can conduct. The constructions seemed hard even to USAJMO level and lacked motivation. The normal trig took way too much time and this solution took even more. The question is a straightforward and brutal one when using ptolemy, all the conditions given and inherent are used and it guarantees a solution.
Video Solution
~MathProblemSolvingSkills.com
See Also
| 2022 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 14 |
Followed by Last Problem | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. ![]()